风振分析通常有时域法和频域法。由于索网结构具有非线性和频率密集性，采用随机模拟时程分析方法。根据风荷载的统计特性进行计算机模拟，采用P阶自回归滤波技术，人工生成具有特定频谱密度和空间相关性的风速时程（激励样本）；根据激励样本在时域内采用Newmark方法和Newton－Raphson法求解动力微分方程，得到响应样本；对响应样本进行统计分析求得风振响应的均值、均方差和相应的频谱特性。

大跨空间结构三维尺寸相近，风速时程具有时间和空间相关性。水平脉动风速谱采用Davenport功率谱；空间相关函数采用Davenport指数衰减形式函数以上式中n为频率（Hz），k为地面阻力系数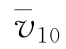，为10m高度处平均风速（m／s），z为受风点高度（m），v－z为z高度处平均风速（m／s），Cx、Cy和Cz为Davenport指数衰减形式函数的指数衰减系数，依次取16、8和10。

在风和结构耦合作用方面，在运动方程的风压F（t）中考虑结构振动速度u·（t）对风速v（t）的修正，即风压F（t）根据空气与结构之间的相对速度来计算，以部分考虑风和结构的耦合作用。(www.daowen.com)

式中，M为质量矩阵；K为刚度矩阵；C为Rayleigh阻尼矩阵，其中ωi、ωj、ζi和ζj分别为第i阶和第j阶模态的自振圆频率和阻尼比。