自1970年以来，相关领域已经发展了多种适用于重复性项目的项目调度方法，这些方法被通称为“线性调度技术”。其中LOB 是一种常见的方法，该方法允许操作的平衡以保证每一项活动的持续运行。作为一种资源型技术，LOB用一种容易理解的图形格式表示生产率与持续时间，其主要优点是在保持工作资源持续性的同时，可以一目了然地显示活动的施工速率和调整速度。由于连续活动是平衡线方法的基本假定，因此学者们一直试图结合CPM 法与LOB 法二者的优点。Hegazy &Wassef（2001）通过整合LOB 和CPM 方法，提出了一个最小化总造价的模型，该模型能够在项目特定期限及多种建造方法条件下，进行工期-造价的权衡分析，但该模型只能考虑三个紧前紧后工作。Arditi et.al.（2002）提出了一个基于CPM 方法的重复调度模型。该模型用一种简单的非图形方式来调度重复性资源，然而该模型不适用于单个活动需要多种资源的情况。Ammar（2003）提出了一个模型用于决定非序列重复活动的不同类型的浮动价值。该模型假定一个活动只使用一种资源。Lucko（2008）使用一个奇异函数来计算线状建设项目的浮动值。

1.LOB 方法简介

LOB 方法的基本表示方式如图4-14 所示。图中每一个栏代表一项活动，同时每一项重复性工作用一条水平线表示，每一栏的宽度代表一个单位的活动时间，任意一个工作单元与活动栏在活动的起点时间和结束时间处水平相交。该方法假定所有的活动都相等，虽然这种假设并不正确，但对那些具有大量重复性单元的项目而言这种假设也有它的现实价值。这种假设就意味着可以在同一项工作中使用多个工作组，如图4-14 所示。LOB 方法通过保持工作的连续性在最小化工作的中断时间的同时可以最大化学习曲线的效益。

图4-14　LOB 的基本原理

2.整合LOB-CPM 的重复性项目调度模型

在建立整合模型的过程中，必须吸收CPM 方法的分析能力以及LOB 方法能够考虑多个工作组以及工作持续性的优点。模型建立在两个基本假设的基础上：首先假定所有工作单元每一个重复性活动的数量是相同的；这就意味着所有重复性工作单元的持续时间是一个常数。其次，采用了如图4-14 所示的班组移动假设。

调度模型的建立共包括四个基本步骤：第一步，平衡线计算；第二步，计算活动持续时间；第三步，确定工序之间的逻辑关系；第四步，进度的安排。

1）平衡线计算

进行平衡线计算的目的是通过确定重复性活动工作组的数量来获得资源平衡的项目进度计划，计算每一道工序的施工速率以满足预定的项目工期并维持班组的连续作业。假定每一道工序上只有一个班组在施工，该班组在完成上一个工作单元之后再进入到下一个重复的工作单元开展施工。

如图4-15 所示，一个重复性项目可以划分为N 个重复工作单元，假定每一个单元的施工速率 Rd保持不变，项目总工期Tp 等于第一个工作单元的关键线路持续时间T1 与其他N-1 个单元持续时间之和。对于关键线路上的重复性工作而言，施工速率 Rd可按照式（4-1）计算得出。

而处于非关键线路上的工作，其总时差可以用来减少施工队伍的投入数量，非关键线路上活动i 的理论施工速率 Rdi可按式（4-2）计算得出。式（4-2）中，TFi表示按照第一个工作单元CPM 网络计算出来的工序i 的总时差。

如图4-16 所示，工序i 每一个施工单元的施工持续时间可按公式（4-3）进行计算，而为了保证工序i 的施工速率所需的施工班组数量Cdi可以根据公式（4-4）计算得出。在大多数情况下，根据公式（4-4）计算出来的施工班组数量不大可能是一个整数，因此施工班组的数量必须按照公式（4-5）来进行四舍五入变成整数，同时取整以后的班组数量Cai还必须满足不得大于该项活动队伍的最大限额的限制。而修正以后的工序i 的实际施工速率Rai还应根据公式（4-6）进行进一步的修正。

图4-15　项目施工速率　

图4-16　多班组同步及持续施工

Cdi=d i×Rdi　（4-4）

Cai=round-up(Cdi)　（4-5）

Rai=Cai/di　（4-6）

2）工作持续时间计算

整合模型主要通过搭接活动的设置来表示重复性工作。为了实现这个目标，假定所有重复性工作的每一个单元都持续时间是一个常数。通过基础的平衡线计算，每一个单元工作的持续时间可以根据图4-17 计算如下：

式中STiN代表最后一个单元的开始时间，ST1i表示第一个单元的开始时间，Di表示工作i 的单元活动持续时间。

图4-17　单元工作持续时间

3）工序间逻辑关系的确定

本模型以维持工作连续性为前提来指定工序间逻辑关系的类型，而不同工序间的逻辑关系通常是按照每项活动的施工速率来决定的。为了建立工序间的逻辑关系，首先必须将指定的活动i 的实际施工速率与后续活动s 的施工速率进行比较。分别用Rai 和Ras 表示活动i 与活动s 的实际施工速率，相应地需要考虑两种情况：

第1种情况：Rai≥Ras

如图4-18（a）所示，工序i 的施工速率要比其后续活动s 的施工速率更快，此时工序i 的第一个单元工作的结束时间决定了后续工作s 第一个单元工作的开始时间。因此可以将这种情况称之为开始—开始关系（Start-Start Relationship，SS 关系）。与SS 关系先联系的工序延迟时间LagSS 可以通过公式（4-8）来进行计算。(www.daowen.com)

LagSS=di+Bis　（4-8）

式中：Bis表示活动i 与s 之间的最小缓冲时间，缓冲时间在平衡线方法中常用于应付不可预见事件导致的项目延迟。SS 关系中与延迟相关的符号含义如图4-18 所示。

图4-18　SS 关系的工序搭接

第2 种情况：Rai＜Ras

如图4-19 所示，在这种情况下后续工序s 的施工速率要比前一个工序i 的施工速率更快。在这种情况下工序i 最后一个工作单元的结束时间决定了后续工作s 最后一个工作单元的开始时间。因此可以将这种情况称之为结束—结束关系（Finish-Finish Relationship，FF 关系）。与FF 关系先联系的延迟　LagFF可以按公式（4-9）进行计算。

LagFF=ds+Bis　（4-9）

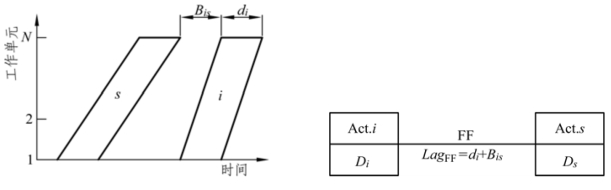
图4-19　FF 关系的重复项目搭接

3.项目进度的总体安排

在完成了平衡线计算、工序持续时间计算并决定了工序间的关系类型之后，就可以按照CPM 的方法计算相关的时间参数了。通过正向传递计算可以得到各工序的最早时间参数，而通过逆向传递计算可以得到各工序的最迟时间参数。

1）正向计算

在正向传递计算过程中，工序的最早时间参数由每一个活动i 所决定。其计算方法如下：

SS 关系：

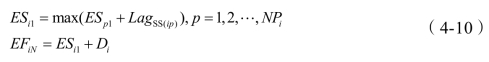
ESi1表示活动i 的第一个单元的最早开始时间，ESp1表示紧前活动p 的第一个单元的最早开始时间，NPi表示紧前活动的数目，EFiN表示活动i 最后一个单元的最早结束时间。

FF 关系：

当一项活动的第一个及最后一个单元的最早开始与最早结束时间确定以后，这个活动所有工作单元的最早开始及最早结束时间可以通过公式（4-12）计算得出。

ESin和EFin分别表示活动i中任意一个单元的最早开始时间及最早结束时间。

2）逆向计算

在逆向计算过程中，需要确定每一项活动i 的最迟时间，最迟时间的计算方法如下：

SS 关系：

LSi1 代表活动i 第一个单元的最迟开始时间，LS s1表示他的后续工作s 第一个单元的最迟开始时间，NSi表示后续工作的数量，LFiN表示活动i 最后一个单元的最迟结束时间。

FF 关系：

当第一项活动第一个单元及最后一个单元的最迟开始及最迟结束时间确定以后，其他单元的最迟开始及最迟结束时间也可以采用公式（4-15）求得：

LSin和LFin分别表示活动i 第n 个单元的最迟开始及最迟结束时间。