1.LSM 方法概述

我国对建设项目的分类有很多标准，比如按照建设性质分为新建工程、扩建工程、改建工程等，按用途可分为生产性项目和非生产性项目。而LSM 方法所研究的对象是沿着线型的路径或空间位置执行的连续施工的线状工程。这类工程的施工活动种类相对土建工程要少得多，各活动有牢固的顺序逻辑，且在执行过程中保证工序的连续性至关重要，像铁路工程、高速公路、地铁、管道工程等，LSM 方法就是以这类线状工程为研究对象的。

LSM 方法自20 世纪80年代出现以来，有了很快的发展。在工程实际中，CPM/PERT 方法的成熟理论及其功能强大的管理软件的广泛使用，使得CPM/PERT 方法占据了市场的主导地位，其他进度计划方法的发展受到很大限制。从1981年Johnston 将LSM 方法应用于高速公路建设工程的进度管理以来，已有很多学者对其进行研究，并取得了一定的成果。而经验告诉我们，LSM 方法未能广泛推广应用的最主要原因是缺少有效的商业化应用软件，从而不能满足建筑业市场的需求。

LSM 方法与CPM/PERT 方法的最大不同在于，CPM/PERT 方法只是从时间一个角度对工程进行计划和控制，而LSM 方法是在一个由时间和空间组成的二维坐标系里表达工程进展情况。它依据线状工程工序施工的时空特点，用一个直角坐标（时间-地点坐标，Time-Location，T-L 坐标）来描述线状工程项目施工的进度计划。水平轴表示线状工程的空间位置，垂直轴来表示线状工程的时间进展情形，根据工序施工的时间和空间位置用一定的图标将工程进展在二维坐标系里表达出来。

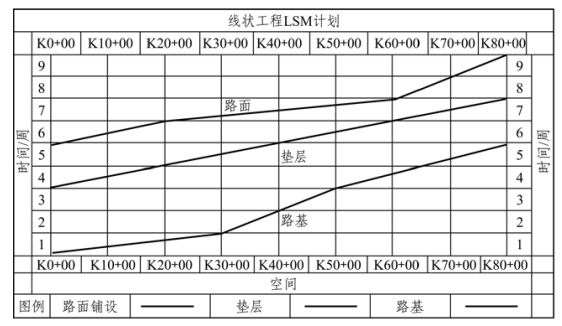
图4-2　线状工程实例

用二维的坐标表达线状工程的进度计划更易理解，更容易让人接受，如图4-2。从该T-L 坐标中可以看出，K30+00 和K50+00 处路基的铺设速度发生变化， 垫层在整段路中的铺设速度不变，路面铺设的速度在K20+00 处由2000 m/周变为4000 m/周，在K60+00 处又减为1000 m/周。LSM 方法能够提供给管理者工序的施工速度何时何地发生变化，是否进行控制等信息。这种计划图不需要大量专业的训练就能识图，直观易懂，便于现场管理人员和施工人员对信息进行分析和采取相应的措施。

2.活动的分类

依据工序施工的时空关系，LSM 方法中的工序可分为三大类：线状工序（Linear Activity）、条状工序（Bar Activity）和块状工序（Block Activity），如图4-3 所示。

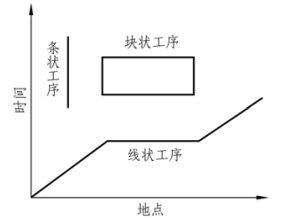
图4-3　活动类型

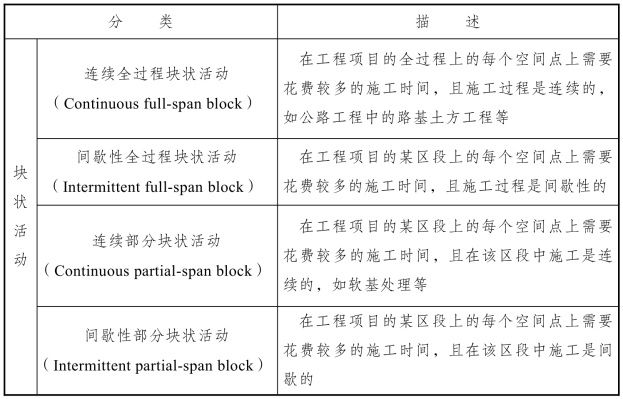
线状工序如市政道路施工中的路基填筑，公路工程中的水泥稳定碎石层铺设、路面铺设等；常见的条状工序有市政道路中的下水井、地下通道的修建等；常见的块状工序有局部软基处理等。下面以一个简单的例子来说明上述工序。例如：某市政工程路基施工有施工准备、局部软基处理、土石方工程、路基碾压、涵洞等工序，用LSM 方法表示如图4-4 所示。

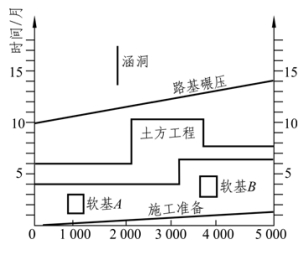
图4-4　活动示例

早期文献中把LSM 计划中的活动简单分为上述三种，而后来的学者对其做了进一步的划分：按照施工活动是否连续、是否贯穿整个项目、是否分段施工，提出了更为详细及符合施工实际的分类方法。

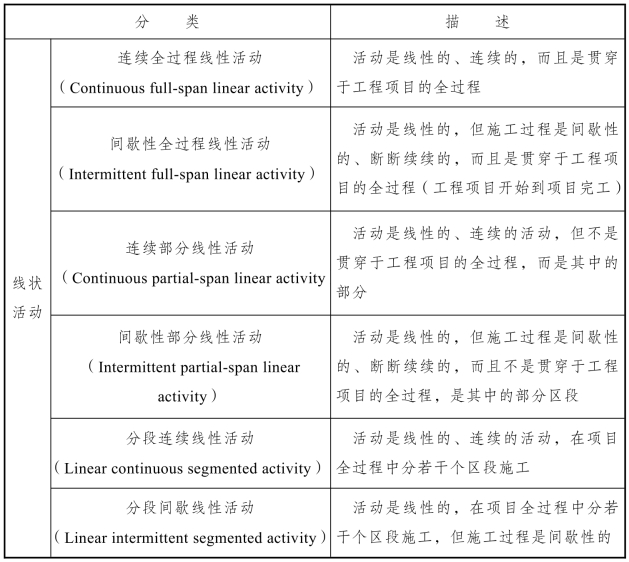
线状活动可分为连续全过程线性活动（Continuous full-span linear activity，CFLA）、间歇全过程线性活动（Intermittent full-span linear activity）、连续部分线性活动（Continuous partial-span linear activity，CPLA）、间歇性部分线性活动（Intermittent partial-span linear activity）、分段连续线性活动（Linear continuous segmented activity）和分段间歇性线性活动（Linear intermittent segmented activity）六种类型。表4-1 对线状活动的具体分类进行了说明。

表4-1　线状活动的划分

条状活动（Bar activity）可分为间歇性条状活动（Intermittent bar activity）、离散型条状活动（Discrete bar activity，DBA）和重复性条状活动（Repetitive bar activity）三种类型。表4-2 对条状活动的具体分类进行了说明。

表4-2　条状活动划分

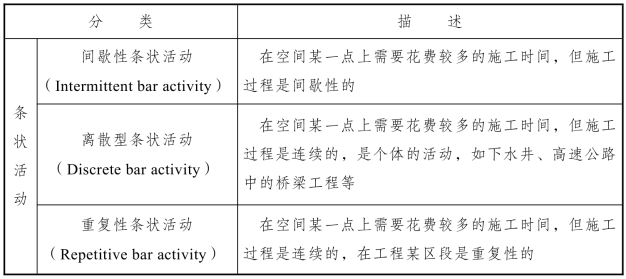
块状活动细分为连续全过程块状活动（Continuous full-span block）、间歇全过程块状活动（Intermittent full-span block）、连续部分块状活动（Continuous partial-span block，CPB）和间歇性部分块状活动（Intermittent partial-span block）四种类型。表4-3 对块状活动的具体分类进行了说明。

表4-3　块状活动划分

以上是LSM 方法对线状工程活动的分类，其表示方法与CPM/PERT 方法有所不同。前者通过活动发生的时间与地点的关系，用二维的线条或者图形来表示其活动，如图4-5 所示。在AOA 中，用箭线表示活动，箭头表示工作流向，节点连接活动，箭线和两端的节点共同表示一项活动。在AON 中，一个节点代表一项活动，箭线代表相邻两活动之间的逻辑关系，只在时间一个维度表示。

图4-5　LSM 方法活动表示

3.关键控制路径

一个有价值的计划必须能够提供一些必要的信息，比如该计划的期望工期、关键路径及工序之间的关系等，便于项目管理人员制定进度目标及进度管理方案等。类似CPM/PERT 方法中的关键路径，LSM 方法也有其关键控制路径（Controlling Activity Path，CAP）。CAP 路径的计算与关键路径法的计算有很大差别，需要先介绍几个相关概念，说明相邻两工序之间的关系。

（1）LT（Least Time Interval）：最短时间间隔，一般发生在相邻两工序中的端点或任一工序施工速度变化的转折点上，在图中沿Y 轴方向。

（2）CD（Coincident Duration）：搭接时间区间，指相邻两工序同时施工的时间区间。

（3）LD（Least Distance Interval）：最小空间间隔，指在搭接时间区间内相邻两工序最短的空间距离，在图中沿X 轴方向。

（4）BB（Beginning Buffer）：相邻两工序开始施工时的时间间隔。

（5）MB（Minimum Buffer）：相邻两工序的最小时间间距。

以上几个概念如图4-6 所示。

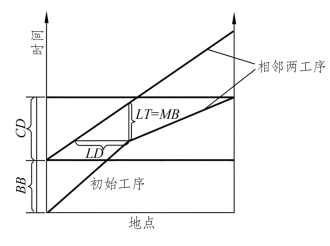
图4-6　LT、TD 等概念图例

关键控制路径（CAP 路径）的确定有以下几个原则：

（1）连续全过程线性活动CFLA 全部或部分区段必为关键工序。

（2）如果相邻CFLA 的CD≠Ø，则其间的任何活动均为非关键工序；如果CD=Ø，则其间的其他工序可能为关键工序，这由这些工序之间的相互关系确定。

（3）可能的关键线路的确定从开始工序开始（即t=0 时刻），到最后工序结束。确定CAP 路径的基本步骤：

①根据施工方案绘制出初始的LSM 进度图，按工序的开始时间，正向顺序找出各工序之间的LT 和LD；

②按照确定CAP 路径的原则，找出可能的关键工序或关键区段；

③从结束工序的终点开始，反向追踪，把关键工序或关键区段用直线连接起来（连接线），确定CAP 路径；

④计算各工序之间的时间参数。

4.活动施工速度差

活动的施工速度差类似于CPM/PERT 方法中的时差的概念。LSM 方法中活动的施工速度差是指该活动可能变为关键活动（段）时可能的施工速度变化值。其可以定义为：某活动的施工速度差是指在不影响相邻两活动的最小间距（Minimum Buffer）的前提下，该活动最小可能的施工速度（the lowest possible production rate）与计划施工速度（the planned production rate）之间的差值。

在CPM/PERT 计划中非关键工序的总时差不为零，关键工序的总时差为零，总时差为零则自由时差必为零。同样，在LSM 计划中，施工速度差只存在于非关键活动（段）中，关键活动（段）的施工速度差为零。在T-L 坐标系中，斜线代表一个线性活动，从斜线的起始位置可以得出计划的开始时间和空间位置，由斜线的斜率可以得出计划的施工速度。活动进行到何时何地都可以用线状活动上的任意一点表示，计划与现实的时空有一一对应的关系。斜线与时间轴夹角的正切值，即该斜线斜率的倒数，就是该线状活动的计划施工速率。活动的计划施工速度可以依据定额得出。当地在建设实践中，由于施工活动中的不确定性，活动的实际施工速度围绕计划施工速度上下波动。

由于施工活动有各个方面的约束，比如施工工艺的要求、不可预见的人为变更、资源是否及时供应等，我们做进度计划时不得不考虑这些因素的影响。假如进度计划安排的过于紧凑，各活动之间相互干扰，势必会影响施工的进度及工程的质量。因此，LSM 计划中相邻两活动之间应该有合理的时间或空间距离，这个距离我们称之为间距（Buffer）。LSM 计划有时间和空间两个维度，所以相邻两活动之间有时间间距和空间间距。时间间距沿Y 方向，有最小时间间距MB（Minimum Buffer）和相连活动开始施工时的间距BB（Beginning Buffer）。最小时间间距LT 代表两道相邻工序间的最小时差。MB、BB 和LT 的定义如图4-6 所示。施工速度差的计算过程如下：

第一步：绘制线状工程项目的LSM 进度计划，确定其关键控制路径CAP。

第二步：找出线性活动的前端非关键活动（段）和后端非关键活动（段）。LSM 计划中，一个线状工序的全部或者一部分是关键活动（段），假如只有一部分是关键活动（段），则其余的是非关键活动（段）。根据关键活动（段）与非关键活动（段）的位置关系，可将非关键活动（段）分为前端非关键活动（段）和后端非关键活动（段），如图4-7 所示。

第三步：在不影响关键路径的前提下，确定前端非关键活动（段）的最早可能开始时间和后端非关键活动（段）最迟必须完成的时间，即前（后）端非关键活动段可能的最低施工速度的位置。

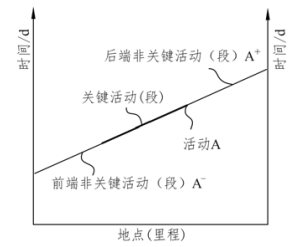
图4-7　非关键活动表示方法

第四步：计算非关键活动（段）的施工速度差RF。

按照施工速度差的定义：

RF=计划施工速度－可能的最低施工速度

5.控制点、最小施工速度和施工速度差

1）控制点及确定方法

（1）控制点（Control Point）：在LSM 计划中，确定非关键活动（段）的最早可能开始时间或最迟必须开始时间时的控制位置。在LSM 计划中，控制点可以用时间来表示，也可以用空间位置来表示。

（2）控制点的确定方法：在LSM 计划中，控制点的位置一般位于：线性活动（段）的端点；关键活动与非关键活动的分界点处；线性活动（段）施工速率变化处；与其他活动有空间约束的位置处。图4-8 分别描述了上述的各种情形。

控制点在线性活动（段）的端点：控制点在线性活动（段）端点的情况有两种，例如图4-8 所示，为了保证关键路径不变，两个全过程线性工序之间的LT 要保持不变，由LT 可确定B 工作的前端非关键活动段B-的最早可能开始时间的控制点及C 活动的后端非关键活动段C+的最迟必须完工时间的控制点。

控制点在关键活动与非关键活动的分界点处：控制点位于关键活动段与非关键活动段分界点处也有两种情况，如图4-9 所示。D 的生产速率比D+的小，为了保证活动D 与活动C 之间的LT 不变，所以D 与D+的交点是控制点，它决定了C 的最迟必须完工时间。(www.daowen.com)

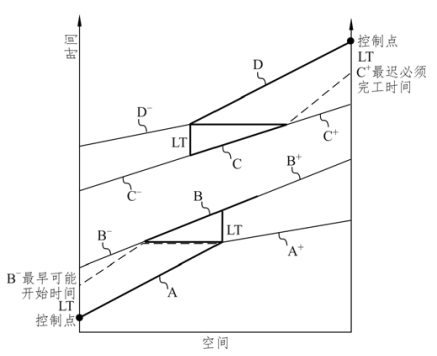
图4-8　控制点位于端点处

控制点在施工速率变化处如图4-9 所示，控制点既是关键活动段与非关键活动段的分界，又是生产速率变化的位置。

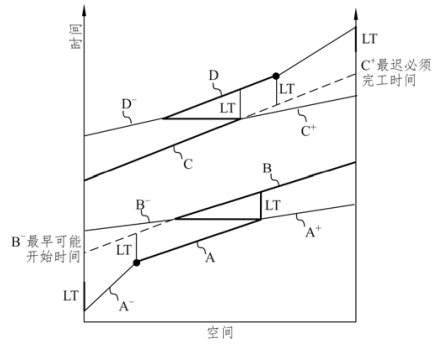
图4-9　控制点位于分界处

控制点位于受其他活动空间位置的约束处：当非关键活动（段）与其他活动有空间上的约束关系时，该活动（段）的最早可能开始时间也会受其影响。如图4-10 所示，因为受到块状活动B 的影响，前端非关键活动段C—的最早开始时间是C′，而不是C″。活动B 的起始坐标和结束时间决定了C—活动只能在C′处开始，假如在C″开始，则会发生在同一时间和地点进行B 和C 两项活动，这不符合必须在B 活动完工以后才能进行C 活动的工艺要求。

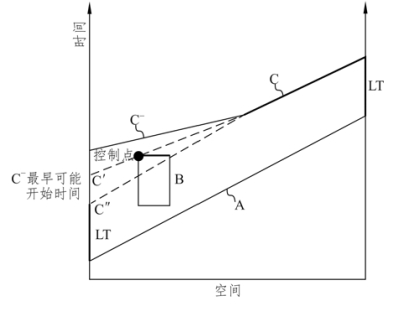
图4-10　控制点位于约束处

2）最小施工速度

由控制点的位置就能够确定前端非关键活动（段）的最早可能开始时间或后端非关键活动（段）的最迟必须完成时间。这两个时间都是对应该非关键活动（段）的最小的施工速度，换句话说就是在组织施工时，在该活动（段）上投入最小的资源量。资源投入量的大小会影响施工速度。但是，最小量并不是无限制的，这个最小的资源量不能影响线状工程项目的总工期。非关键活动（段）的最早可能开始时间和最迟必须完成时间是LSM 计划技术中的重要参数，类似于CPM/PERT 方法中的工序最早开始时间（ES）、最迟开始时间（LS）、最早完工时间（EF）、最迟完成时间（LF）等时间参数。求CPM/PERT 方法的ES 可根据正推法的“沿线累加，逢圈取大”的原则计算出来，求LS 可依据逆推法的“逆线累减，逢圈取小”的原则计算。依据这两个参数可以求出其他几个参数。同理，LSM 计划中的参数也有类似的推理关系。

例如图4-11 所示为一个简单的例子，用这个例子可简单地说明LSM 计划中的前端非关键活动（段）的最早可能开始时间（ES）、后端非关键活动（段）的最迟必须完成时间（LF）及最小施工速度的算法[A 代表非关键活动（段）]。先确定相邻两CLFA 工序之间的LT 和LD，然后确定CAP 路径。找出活动A的后端非关键活动段、活动D 和F 的前端非关键活动（段）。

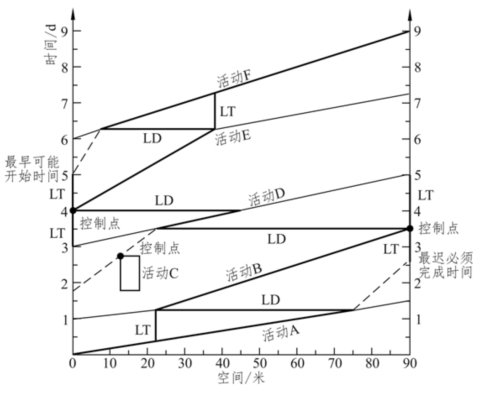
图4-11　最小施工速度

具体步骤为：

（1）找出相邻CLFA 的LT 和LD。

（2）确定CAP 路径。

（3）根据控制点确定方法，找出非关键活动的控制点。

（4）依据步骤③确定的控制点，确定非关键活动（段）的最早可能开始时间或最迟必须完工时间。

（5）计算该非关键活动（段）的最小施工速度。

活动A+的最迟必须完成时刻为关键活动 B 的完成时间减去活动A 与活动B 之间的LT，即：

活动D—受活动C 的空间约束关系，所以D—活动的最早可能开始时间需要计算。已知（3.5，22.5），控制点P（2.75，12.5），设D—的最早可能开始的坐标为，则依据线性关系：

活动F—的最早可能开始时间为关键活动E 的开始时间加上活动E 与活动F之间的LT：

以上是常见位置的非关键活动（段）的最早开始时间或最迟必须完成时间的算法。由这两个参数可以算出相应活动的最小施工速度。

LSM 计划中用（TA，LA）来表示活动A 的所处的时刻和空间位置。该例中活动A 的后端非关键活动（段）A+的开始时空坐标为SA+0（1.25，70.5），结束时空坐标为FA+0（1.5，90），最迟必须完成的时空坐标为FA+1（2.6，90）。正常情况（正常施工指依据原始计划所绘制的初始LSM 计划）下的施工速度：

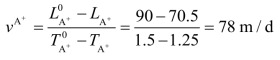
最小施工速度为

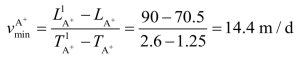
其中：表示A+正常情况下的初始时刻和空间位置，即

表示A+正常情况下的完成时刻和空间位置，即

表示A+最迟必须完工的时刻和空间位置，即

对活动D—，由于受到块状活动C 的空间限制，最早可能开始时间的时空坐标为（1.8，0），正常情况下的开始与结束坐标分别为（3，0），（3.5，22.5）。则D—正常情况下的施工速度为：

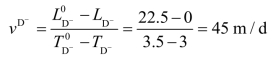
最小施工速度为：

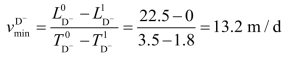
同理可求出F—的正常施工速度及最小施工速度。在关键路径不变的情况下，线状活动i 的施工范围通常是不变的，则施工速度由该活动段的起始时刻确定，即：

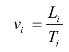
其中：vi——活动i 的施工速度；

Li——活动i 的空间距离；

Ti——完成活动i 所需的时间；

而活动i 的资源需要量为：

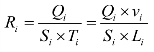
其中：Ri——活动i 所需的资源量；

Qi——活动i 的工程量；

Si——活动i 的产量定额；

由以上可知，线性活动的线形越陡，所需时间越长，施工速度越小，相应所耗费量的资源越少；线形越平，所需时间越短，施工速度越大，相应所耗费的资源量就越多。施工速度不仅影响施工时间，还影响资源需要量，因此，施工速度是LSM 计划中的一个重要参数。

3）施工速度差（Rate Float）

LSM 计划中的施工速度差（Rate Float）的概念类似于CPM/PERT 方法中的总时差（Total Float）的概念。双代号网络计划中的总时差是指一项工作在不影响总工期的前提下所具有的机动时间，是由于工序最迟完成时间与最早开始时间之差大于工序作业时间而产生的机动时间。

LSM 计划中的施工速度差是指相邻两个活动施工速度的差值。由概念可知，某活动的施工速度与其相邻活动的施工速度有关。产生施工速度差的原因有两个方面：一方面是在一定的时空范围以内，某活动的施工速度不受其相邻活动（紧前活动或紧后活动）施工速度的影响；另一方面是在一定时空的范围以内，某活动的施工速度受到其相邻活动（紧前活动或紧后活动）施工速度的影响。前一方面的原因，我们称为自由施工速度差（Free Rate Float，FRF），后一方面的原因我们称为相关施工速度差（Related Rate Float，RRF）。这两种施工速度差之和我们称之为施工速度差。

（1）自由施工速度差（FRF）。LSM 计划中自由施工速度（FRF）差对比网络计划中的自由时差，前者是指在不影响紧后活动正常施工的前提下本活动所具有的施工速度差；后者指在不影响紧后工序最早开始的情况下该工序所拥有的机动时间。根据其定义可得出网络计划方法中自由时差等于紧后工作的最早开始时间与该工作的最早完成时间之差。同理我们可以得出LSM 计划方法中自由施工速度差的计算方法，即正常施工时的速度与不影响紧后工序正常施工时的速度之差。LSM 计划中自由施工速度差如图4-12 所示。根据定义，自由施工速度差为：

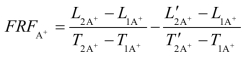
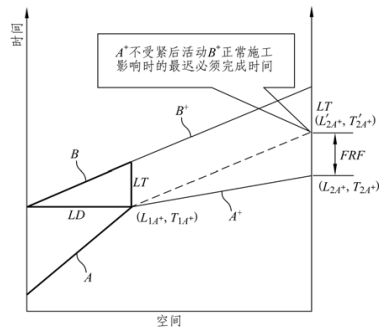
图4-12　施工速度差示意图

（2）相关施工速度差（RRF）。相关施工速度差（RRF）指在紧前或紧后活动可以提前或推迟的情况下，该活动还可以以更小的施工速度施工。如图4-13所示，B+在不影响关键活动C 的情况下本身还具有自由时差，这个自由时差对A+的最迟完工产生影响，使得A+在不影响B+施工的前提下还可以再推迟，这时的与B+相关的施工速度差就是A+的相关速度差，由定义知A+的相关速度差为：

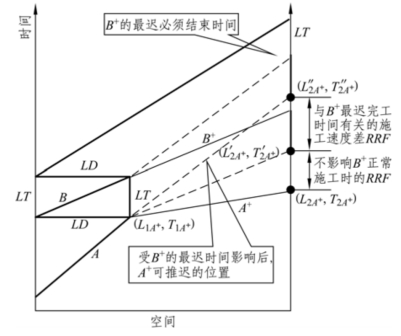
图4-13　FRF 与RRF

（3）施工速度差（RF）与自由施工速度差（FRF）及相关速度差（RRF）的关系。施工速度差的定义：在不影响整个工期的前提下，该工序所拥有的速度差。显然，它包括自由施工速度差和相关施工速度差。依据施工速度差的定义可知：

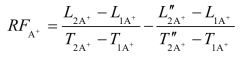
施工速度差是自由施工速度差和相关施工速度差之和。施工速度差类似于网络计划中的总时差（TF）。所以，关键活动（段）的施工速度差为零，同时，自由速度差和相关速度差也必须为零。只有非关键活动（段）的速度差不为零。