根据7.4.1 的模糊PID 控制原理来设计全地形车悬架模糊控制策略。 为获得较好的控制效果，将模糊控制器的输出设定为ΔP、ΔI 和ΔD，则PID 控制器的输入为P＋aΔP、I＋bΔI 和D＋cΔD，其中P、I 和D 为初始值，a、b 和c 为模糊控制器的输出量化因子。

由模糊PID 的原理可知，模糊PID 控制的关键是模糊规则表的制作。 一般情况下，PID 参数的整定规则为：当｜e｜比较大时，为使系统具有较好的快速跟踪性能，应取较大的Kp 与较小的Kd，同时为避免响应出现较大的超调，应对积分加以限制；当｜e ｜处于中等大小时，为使系统响应具有较小的超调，Kp 应取得小些，Ki 和Kd 的大小要适中，以保证系统的响应速度；当｜e｜较小时，为使系统具有较好的稳态性能，Kp 和Ki 均应取得大些，同时为避免系统振荡，并考虑系统的抗干扰性能，当｜ec ｜比较小时，Kp 值要取大些，反之，应取小些。

按此调整规律，先确定初始值Kp、Ki 和Kd，然后结合调试过程中的经验来确定的模糊规则表。 表7.2、表7.3、表7.4 分别为ΔKp、ΔKi、ΔKd 的控制规则表。

表7.2　ΔKp 控制规则

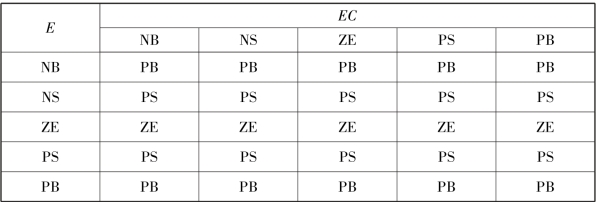
表7.3　ΔKi 控制规则

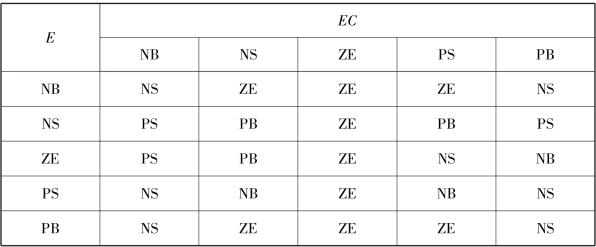
表7.4　ΔKd 控制规则

(www.daowen.com)

对PID 控制器中的参数Kp＋aΔKp、Ki＋bΔKi 和Kd＋cΔKd 则可通过模糊控制器的输出量ΔKp、ΔKi、ΔKd 来实时在线自整定，则可实现模糊PID 控制。 模糊控制器的输入变量为簧上质量加速度 z··2 与期望的簧上质量加速度 z··opt之间的误差及其误差变化率作为输入变量，这里设期望的簧上质量加速度为0。

将误差的论域定义为［－3，3］，语言变量分为5 个子项｛负大（NB），负小（NS），零（ZE），正小（PS），正大（PB）｝。 模糊子集的隶属函数采用灵敏度较高的三角形函数。

将误差变化率的论域定义为［－6，6］，语言变量分为5 个子项｛负大（NB），负小（NS），零（ZE），正小（PS），正大（PB）｝。 模糊子集的隶属函数同样采用灵敏度较高的三角形函数。

3 个模糊控制器的输出分别为ΔKp、ΔKi、ΔKd。 其中ΔKp 论域定义为［0，3］，其论域上有3 个语言变量值｛零（ZE），正小（PS），正大（PB）｝；ΔKi 的论域定义为［－3，3］，其论域上有5 个语言变量值｛负大（NB），负小（NS），零（ZE），正小（PS），正大（PB）｝；ΔKd 的论域定义为［－1，1］，其论域上有5 个语言变量值｛负大（NB），负小（NS），零（ZE），正小（PS），正大（PB）｝。 图7.9 为ΔKp 的模糊推理决策结果。

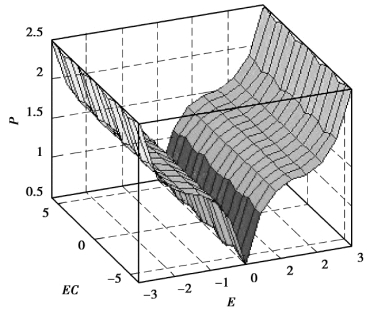
图7.9　ΔKp 的模糊推理决策结果

与模糊控制一样，对后左悬架和后右悬架进行单独控制。 联合仿真模型中ADAMS子模块包含2 个输入和6 个输出，2 个输入为后左悬架及后右悬架的控制力，6 个输出分别为后左悬架、后右悬架上方位置的振动加速度及上下方位置的振动速度。 模糊控制器偏差e、变化率ΔKp、ΔKi 和ΔKd 量化因子分别为3、0.04、20、1、0.1，模糊PID 控制器中Kp、Ki 和Kd 的初始值为120、7、0.1。