摩托车车架是整个摩托车的骨架，发动机是摩托车的动力源，也是主要激励源。 与车架相比，质量大，对车架挂发动机的结构动态特性有很大的影响，因此应分析车架挂发动机的结构动态特性。

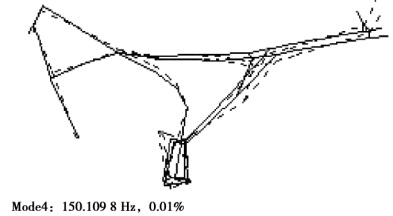
图4.17　车架的四阶实验模态振型

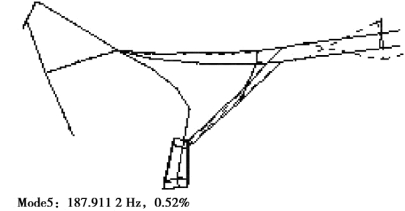
图4.18　车架的五阶实验模态振型

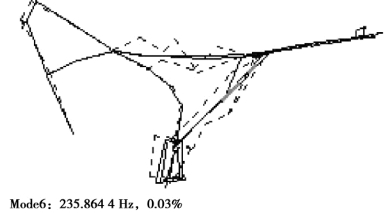
图4.19　车架的六阶实验模态振型

在建立车架挂发动机的有限元模型中，由于发动机模型结构复杂，且我们关心的频率是在250 Hz 以内，发动机本身的模态对车架挂发动机的模态影响不大，但是发动机的转动惯量、质心位置、质量对车架挂发动机模态影响很大。 在本书中，通过发动机的三维模型计算出发动机的转动惯量IXX、IYY、IZZ。 将发动机简化为一个质点，通过NASTRAN中RBE2 将发动机与车架刚性地连接在一起，建立车架挂发动机有限元模型，如图4.20所示。

将车架挂发动机的有限元模型提交MSC.NASTRAN 进行自由模态分析，利用兰索斯法提取前6 阶模，见表4.3，前6 阶振型如图4.21—图4.26 所示。

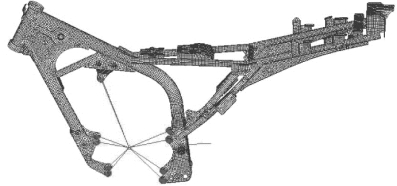
图4.20　车架挂发动机的有限元模型

表4.3　车架挂发动机计算模态分析结果

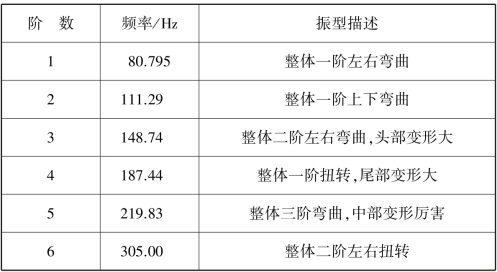
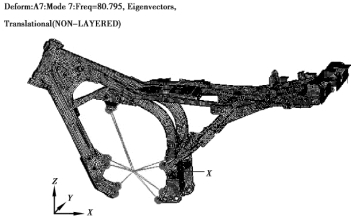
图4.21　车架挂发动机一阶计算模态振型

比较车架和车架挂发动机的六阶振型可以看出，挂上发动机以后振型和频率都发生了明显的变化，车体的一阶振型由一阶上下弯曲变为左右弯曲，而二阶振型由左右弯曲变为上下弯曲。 且一阶上下弯曲的频率由89.9 Hz 提高到了111.29 Hz，一阶左右弯曲频率由98.75 Hz 下降到了80.795 Hz。 这是由于挂上发动机以后虽然车体的质量增加了，但是车架的上下弯曲刚度增加的效果更加明显，从而提高一阶上下弯曲的频率；左右弯曲频率的降低是发动机的质量的影响大于其刚度的影响。 从而可以看出，发动机对车体的结构动态特性有很大的影响。

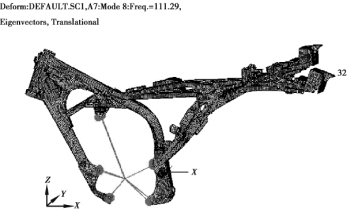
图4.22　车架挂发动机二阶计算模态振型

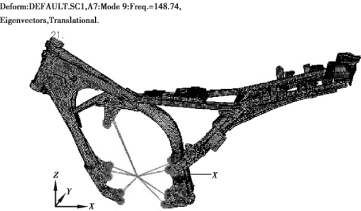
图4.23　车架挂发动机三阶计算模态振型

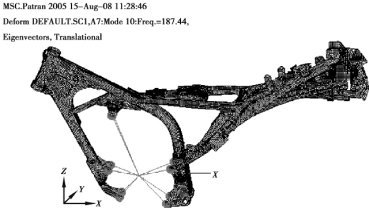
图4.24　车架挂发动机四阶计算模态振型

车架挂发动机总成实验模态测点布置如图4.27 所示。 根据实测的激励信号和响应信号，按照Hv 法估计频响函数矩阵，在感兴趣的频率范围内根据稳态图（图4.28），利用polymax 模态识别法识别系统极点，估计振型。(www.daowen.com)

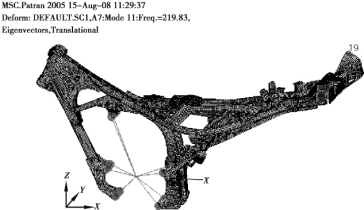
图4.25　车架挂发动机五阶计算模态振型

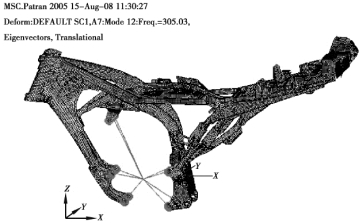
图4.26　车架挂发动机六阶计算模态振型

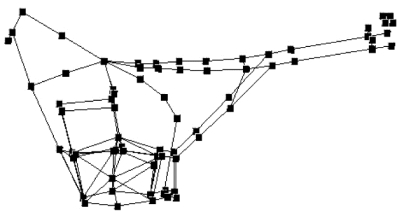
图4.27　测点布置图

车架挂发动机的实验模态振型如图4.29—图4.34 所示，各阶模态振型描述如下：一阶模态振型为整体一阶左右弯曲；二阶模态振型为整体一阶上下弯曲；三阶模态振型为整体二阶左右弯曲，头部变形明显；四阶模态振型为整体一阶扭转，车架尾部变形厉害；五阶模态振型表现为整体三阶弯曲，车架中部变形厉害；六阶模态振型为整体二阶左右扭转。

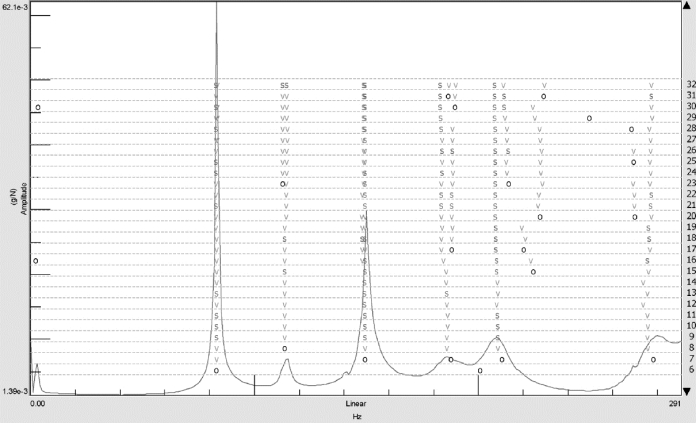
图4.28　频响函数之和的稳态图

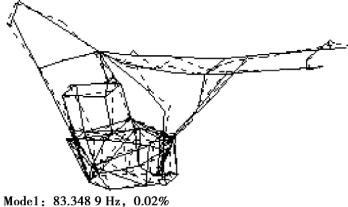
图4.29　车架挂发动机的一阶计算模态振型

图4.30　车架挂发动机的二阶计算模态振型

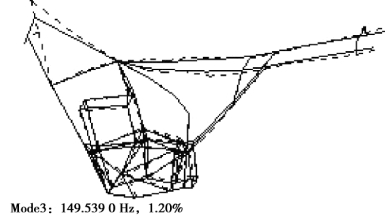
图4.31　车架挂发动机的三阶计算模态振型

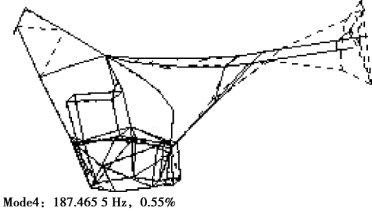
图4.32　车架挂发动机的四阶计算模态振型

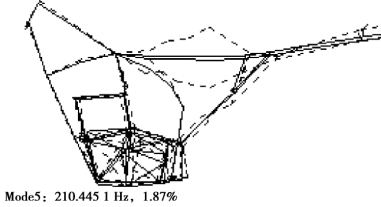
图4.33　车架挂发动机的五阶计算模态振型

图4.34　车架挂发动机的六阶计算模态振型

对比车架挂发动机计算模态和实验模态结果可以看出，它们之间的差别很小，最大的频率差别低于10%，说明车架挂发动机有限元模型的建立是比较准确可靠的。