按照4.1 的结构动态特性分析方法。 先以某款摩托车为例进行结构动态特性分析。

根据二维设计图纸利用UG4.0 建立的摩托车车架的几何模型。 车架的有限元模型既要反映车架实际结构的力学特性，又要尽可能地减少单元的数目。 因此，在建立车架的几何和有限元模型时应做如下考虑：

①几何模型简化：车架上布置了很多对结构特性没有影响的附件，但会使划分网格的工作量变大，求解时间变长，甚至影响模型的有限元划分质量，因此，需对模型进行合理的简化。

②该车架的主要结构为钢板、圆管，其厚度与长度和截面尺寸相比很小，因此用MSC.NASTRAN 中的shell 单元来离散车架结构，抽取模型各个部件的中面然后在HYPERMESH 中进行面的缝合和修补。

③为保证模型的准确性和可靠性，同时兼顾计算效率，整体采用quad4 单元。

④车架上一些部件是焊接在一起的，建模时忽略焊接的影响，直接用shell 单元将各部件连接在一起。

⑤为保证模型的准确性，所划分的单元应满足一定的要求（斜度、翘曲度、边长比、雅可比等）。

将三维几何模型转化为igs 格式导入Hypermesh 中，完成有限元前处理，建立了有限元模型，有限元模型包含34 011 个节点，30 911 个单元，其中tria3 单元即三角形单元占比例为4.3%。 模型如图4.5 所示。 车架材料为优质碳素钢，弹性模量为2.06E11 N／m2，材料密度为7 850 kg／m3，泊松比0.3。

图4.5　车架有限元模型

将摩托车车架有限元模型导入MSC.NASTRAN 中，采用兰索斯法计算车架的自由模态，即可提取前六阶模态参数，见表4.1，振型如图4.6—图4.11 所示。

表4.1　车架计算模态分析结果

图4.6　车架的一阶计算模态振型图

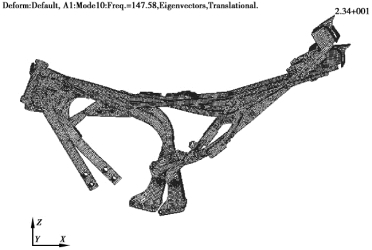
图4.7　车架的二阶计算模态振型图

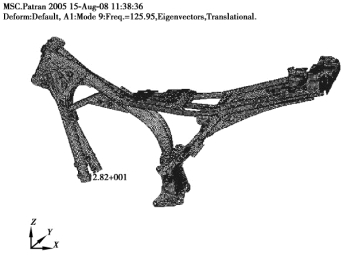
图4.8　车架的三阶计算模态振型图

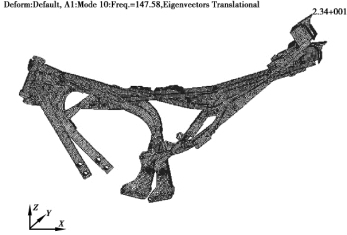
图4.9　车架的四阶计算模态振型图

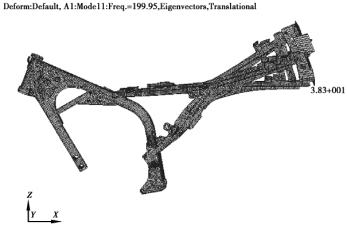
图4.10　车架的五阶计算模态振型图

如上所述，在有限元建模过程中采用了许多假设和简化。 因此，模型的准确性需要通过试验来验证。(www.daowen.com)

对摩托车车架进行模态试验，首先应合理确定测点和激励点。 测点的布置对实验结果的正确性有很大的影响，测点的布置原则为：布置在悬架支点、车架连接点和刚度变化较明显的点上；尽可能地使车架主梁布点均匀；另外，布点还应根据实验数据灵活地进行调整，以获得较精确的数据。 激励点应能激起所关心频率范围内的模态，可以是多个激励点，也可以是一个激励点，车体布点图如图4.12 所示。

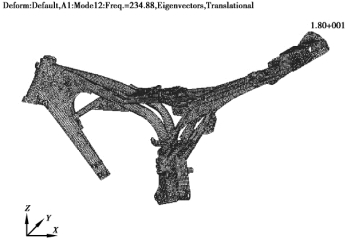
图4.11　车架的六阶计算模态振型图

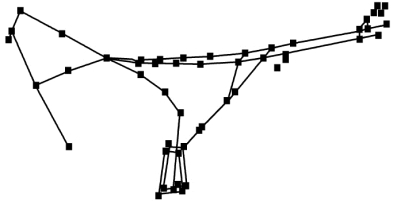
图4.12　车体布点图

根据实测的激励信号和响应信号，按照Hv 法来估计频响函数矩阵，在感兴趣的频率范围内借助稳态图，利用最小二乘复指数法识别系统极点，再利用最小二乘频域估计振型，然后通过模态置信准则来检验模态。

最小二乘复指数法是时域分析方法，脉冲响应函数由频响函数逆变换得到，为避免带外模态的影响，频响函数在所选频带的起始点和终止点的值应很小，实验得到的频响函数之和如图4.13 所示。

最后估计得到实验模态振型的MAC 矩阵，表4.2 所示各阶之间的MAC 都小于10%，说明各阶模态的正交性较好，表明模态试验结果是比较准确的。

表4.2　模态判定准则（MAC）

续表

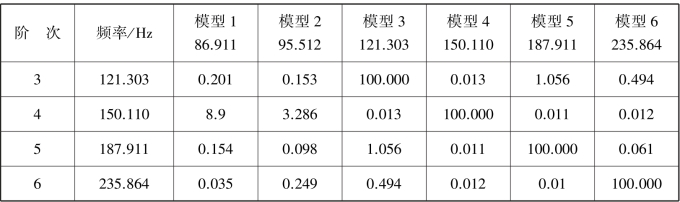
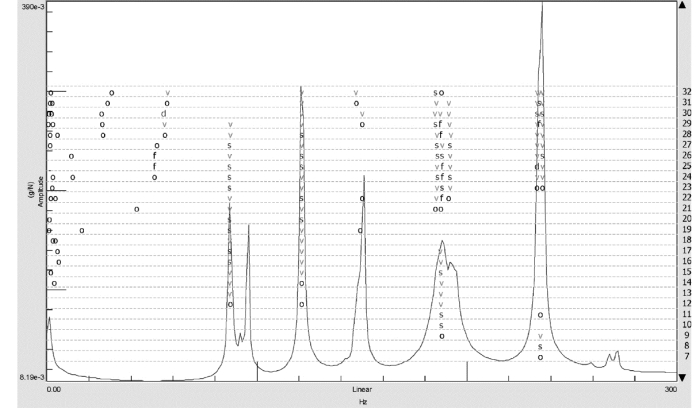
图4.13　频响函数之和的稳态图

通过模态判定准则数值大小说明所估计的模态参数比较合理、准确。

车体的实验模态的振型图如图4.14—图4.26 所示，各阶振型描述如下：一阶模态为一阶上下弯曲；二阶为左右弯曲，头部变形明显；三阶模态为三阶左右弯曲；四阶模态为二阶上下弯曲；五阶模态为一阶左右扭转，尾部变形大；六阶模态为整体的二阶扭转。

对比车架的有限元模态分析可以看出，车架的计算模态振型和频率与车架的实验模态得到很好的吻合，说明车体模型的建立是比较准确的。

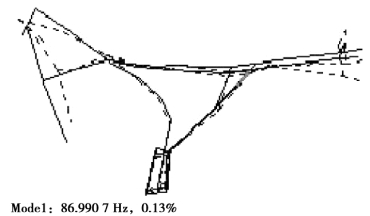
图4.14　车架的一阶实验模态振型

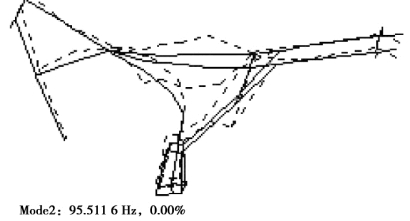
图4.15　车架的二阶实验模态振型

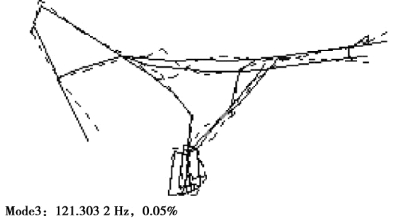
图4.16　车架的三阶实验模态振型