水,是人们认为最普遍的东西,也是最熟知的了;其实不然,你对它有多少了解,请往下看。一杯水若放大几百万倍,就会看到它具有明显的颗粒结构,是由大量紧紧地挨在一起的单个分子组成的,这些分子绝不是处于静止状态,而是处于猛烈的骚动之中,它们来回不停地运动,互相推挤,恰似一个极度激动的人群。水分子或其他一切物质分子的这种无规则的运动称为热运动。

如果把液体加热,则其中悬浮小微粒的狂热推挤将会显得更加激烈;如果冷却下来,则推挤骚动现象就会渐渐缓慢下来,这就是物质内部的热运动。因此,我们通常所说的温度不是别的,正是分子运动激烈程度的量度。通过对热运动与温度的关系的研究,人们发现在温度达到-273℃时,物质的热运动就会完全停止。这时,一切分子都归于静止,这就是最低的温度,人们称它为绝对零度。如果有人提出更低的温度,那显然是荒唐的。这是因为哪里会有比绝对静止更慢的运动呢?

摄氏温度t与热力学温度T之间的数值关系为：

一切物质的分子在接近绝对零度时,能量都是极小的。因此分子之间的内聚力会把它们紧紧地聚集成固态的硬块。这些分子只能在凝结状态下轻微地颤动。如果温度升高,这种颤动就会越来越强烈;到了一定程度,物质由固体就变成了液体。物质的熔解温度取决于分子内聚力的强度。

下面列举一些物质元素的温度变化情况：

氢气(H2) 在-259.2℃下处于固态,在-253℃沸腾;

水(H2O)在0℃下结冰(称为冰点),在100℃时开始沸腾(称为沸点);

冰熔点为0℃(冰是固态水,在0℃时开始融化);

氧气(O2)熔点为-218.4℃,沸点为-183℃;

氮气(N2)熔点为-210℃,沸点为-196℃;

铅(Pb)熔点为327.5℃,沸点为1749℃;

铁(Fe)熔点为1535℃,沸点为2861℃;

锇(Os)熔点为3045℃,沸点为5027℃。

液体的气化也和固体的熔化一样,不同的物质有不同的温度;一般物质的熔点越高,它的沸点也就越高。

物质的温度如果不断地升高,就会威胁到分子本身的存在。因为这时候分子间相互碰撞就变得十分猛烈,有可能把分子撞开,使分子成为单个的原子。

在这种被称为热离解的过程中,当温度达到几千摄氏度时,分子就不复存在了。整个世界就将是纯化学元素的气态混合物。

在太阳表面上,情况就是这样,因为太阳表面温度大约有6000℃。在高温下,猛烈的热碰撞不仅能把分子离解成为原子,而且还能把原子本身的外层电子去掉,这种现象叫作热电离。进一步,如果温度再升高达到几万摄氏度,甚至达到几百万摄氏度的极高温度(超过实验室中所能获得的最高温度,这在包括太阳在内的恒星内部是屡见不鲜的),此时热电离就会越来越占优势。最后,原子也完全不能存在了。

为了使物质彻底热电离,使原子核分解为单独的核子(质子和中子),温度至少要升高到几千亿摄氏度。这样的极高温度,目前即使在最热的恒星内部也还未发现(太阳的中心部分温度也只有2000万摄氏度),太阳能主要是由碳、氢循环产生的,而恒星的生命来自氢到氦的缓慢的核嬗变过程。当恒星还年轻,刚刚由星际弥漫的物质形成时,氢元素的比例超过了整体质量的50%。我们可以预料到,它还有极长的寿命。例如,根据太阳的光度,人们能判断出太阳每秒钟要消耗450万吨氢及其他。太阳的质量是2×1027t,其中有一半是氢,因此太阳的寿命理论上至少还有几百亿年。

由于太阳的总质量是如此巨大,所以太阳还可以照耀人类千秋万代。地球每分钟获取太阳的能量同太阳总辐射能量的比值大约是。由此可见,地球获得太阳的能量是极小的一部分,也就是说,地球所获得的太阳能仅仅相当于太阳向宇宙空间辐射总能量的二十二亿分之一,然而就是这极小部分的太阳能,足以维持着地球上各种自然现象的进行,尤其是靠此求得生存的生命物质。伟哉,人类的太阳!奇哉,浩瀚的宇宙!(www.daowen.com)

热冲击的结果使得按量子力学定律建立起来的精巧物质结构逐步被破坏,并把这座宏伟大厦变成乱糟糟的一群瞎撞乱冲、看不出任何明显规律的粒子。对于完全不规则的热运动,有一类叫作无序定律(统计定律)的新定律在起作用。

例如,太阳的能量是由它内部深处的元素在核嬗变时产生的,这些能量以强辐射的形式释放出去。这些“光微粒”或者称为“光量子”,从太阳内部向太阳的表面运动。光速是每秒约30万千米,太阳的半径是70万千米。因此,如果光量子走直线的话,只要两秒多钟就可以从太阳的中心走到太阳的表面。但是事实上不是这样的。光量子从太阳中心向外行进时,要与太阳内部无数的原子和电子相互碰撞,光量子在太阳内的自由行程约为1cm(比分子的自由行程长多了),由于太阳的半径是如此之大,也就是约700亿厘米,这样,光量子就得像醉汉那样拐上多个弯,也就是光量子要想走到太阳表面,从内部中心开始需要拐上(7×1010)2个弯,才能到达太阳表面。这样,每一段路需要花3×10-11s,而整个行程所用的时间即为3×10-11×(7×1010)2≈1.5×1011s,也就是需要花5000年左右。通过此例我们看到扩散过程是何等的缓慢,光量子从太阳中心走到太阳表面竟然要花上5000年左右才能到达,而从太阳表面光线穿越星际空间走直线到达地球,却仅仅只需要8min18s就够了。

我们在前面的一些讨论,只不过是把概率的统计定律应用于分子运动的一些简单例子。深入一步讨论,可以了解更重要的熵定律,它是总辖一切物体,小到一滴液体,大到由恒星组成的宇宙中一切有关热行为的重要定律。

让我们先复习一下计算各种简单和复杂事件的可能性(即概率)的方法。

例如,投掷硬币的时候正反面向上的概率是服从正态分布的。如果掷100次,可以有把握地判断正面向上的次数大致会接近50次。但是如果只掷4次。正面向上就可能出现3次或1次。实验次数越多,概率定律就越精确,这时它才成为一条法则。

在日常生活中计算概率,当要计算的对象数目很少时,这种推算往往是不准确的;而当数目增多时,就会越来越准确。这就使得在描述由多得数不清的分子或原子组成的物体时,概率定律就显得特别有用了。

例如,当你坐在房间里看书时,整个房间里都均匀地充满着空气。你可能从未遇到过这些室内的空气突然自行聚拢在房屋中的某一个角落,从而使你呼吸不到空气而窒息在椅子上的这种意外情况。不过,这件令人恐怖的事情并不是绝对不可能的,它只是极不可能产生罢了。

为了弄清这一点,设想有一个房间,被一个想象中的垂直平分面分成两个相等的部分。这时,空气分子在这两个部分中最可能出现什么样的分布呢?这个问题和前面我们提到的投掷硬币的概率一样。任选一个单独分子,它位于房屋里左半边或右半边的机会都是相等的。在不考虑彼此间作用力的情况下,第二个、第三个以及其他所有分子处在房间里左半边或右半边的机会也都是相等的。也就是一半对一半的分布是最有可能的。当数目很大时,可能性就变成了必然性。

在一间60m2的房间里,大约有各种气体分子1027个。由于气体分子间距离很大,空间并不拥挤,所以在一定体积内虽然已经有一大堆分子,却并不影响其他分子的进入。例如,有一间体积为5×107cm3的房间,可以容纳5×104g空气,空气分子的平均质量为30×1.66×10-24 g≈5×10-23g,所以总分子数为：=1027(个)。

这些分子同时聚集在房间右半边(或左半边)的概率为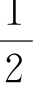：()1027≈10-3×1026,也就是1对103×1026。(简单地说,就是“几乎为零”)

而另一方面,空气分子以每秒0.5千米左右的速度运动,因此,从房间一端跑到另一端只要0.01s,这就是说,在1s内,房间里的分子就会进行100次重新分布。于是要得到完全处于右半边(或左半边)的分布,就需要等待10299999999999999999999999998s。

这个数字之大真是无法形容,要知道,据理论推算宇宙的年龄迄今为止,也只有1017s。所以,你可以安心、安静地接着看你的书,不必去担心突然产生窒息而死的灾难。

因此,我们可以说：一切依赖于分子无规则热运动的物理过程,都朝着概率增大的方向发展,而当过程停止,即达到平衡状态时,也就达到了最大的概率。在前面所举房间内部气体分子分布的例子中,我们已经看到,分子各种分布的概率往往是一些很不方便计算的小数据(如空气聚集在半间屋子里的概率约为10-3×1026),因此,在进行计算时,我们一般都取它们的对数。这个数值就称为“熵”。“熵”在所有与物质无规则热运动有关的现象中起着主导作用。

至此,我们可以将前面那些有关物理过程中概率变化的叙述改写如下：

一个物理系统中任何自发的变化,都朝着使熵增加的方向发展,而最后的平衡状态,则对应于熵的最大可能值。

这就是著名的熵定律,也称为热力学第二定律(热力学第一定律就是能量守恒定律)。

从以上所举的例子中可以看出,当熵达到了极大值时,分子的位置和速度都是完全无规则地分布着,任何使它们运动有序化的做法都会引起熵的减小。因此,熵定律又称为无序加剧定律。

熵定律及其一切推论是建立在以数量极大的分子为对象的基础上的,这样,所有基于概率的推测,才会变为几乎绝对肯定的事实。如果物质的数量很少,这类推测就不那么可信了。因为在小范围内,在数量很小时,气体分子的分布是十分不均匀的。如果能把分子放得足够多,即把气体分子的数量放得足够大,我们将会看到,分子不断地在某个地方较为集中一下子,然后又散开,接着又在其他地方产生某种程度的集中,这种效应叫作密度涨落,它在许多物理现象中起着重要作用。例如,当太阳光穿过地球大气层时,大气的这种不均匀性就造成了太阳光光谱中蓝色光的散射,因而使天空呈现蓝色,同时使太阳光的颜色变得比实际上红一些。这种变红的效应在日落时特别显著,因为这时太阳光穿过的大气层最厚。如果不存在空气的密度涨落,天空则永远是黑色的,人们在白天也能看见天上的恒星。