1）不同栏杆透风率对颤振性能的影响

由于人行道栏杆的形式不同，其透风率也在改变，从而对结构的气动性能存在影响。 为了探索栏杆不同透风率对颤振性能的影响，本书考虑3 种栏杆形式分别进行数值模拟，尺寸依然是在实桥设计值的基础上设置1／60 的缩尺比。 通过改变栏杆的形式分别考虑了3 种工况，即大透风率、中透风率和小透风率。

本节数值模拟的分析参数，包括流场区域的大小、网格划分分区以及FLUENT 分析基本参数设置均同上节所分析的主梁节段模型一样，3 种不同透风率的栏杆所对应网格的划分情况如图5.20 所示。

图5.20　3 种不同透风率的栏杆所对应网格的划分情况

首先对3 种不同透风率栏杆的压力等高线分布进行考察，如图5.21 所示。

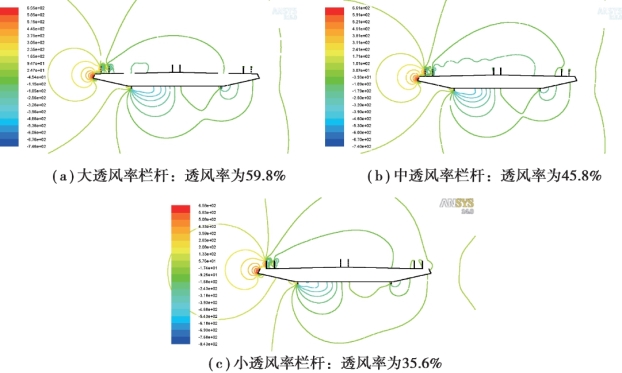
图5.21　3 种不同透风率栏杆的压力等高线分布情况

接着对3 种不同透风率栏杆的速度流线分布情况进行考察，如图5.22 所示。

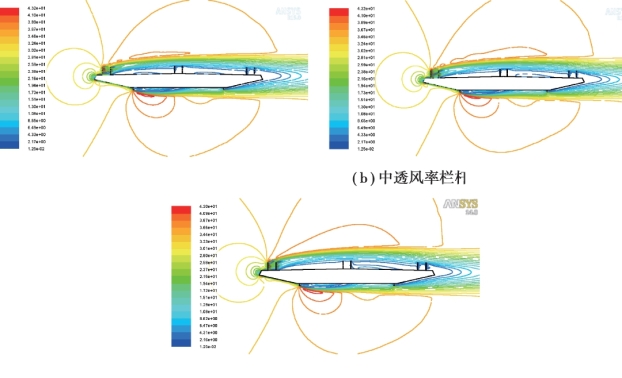
图5.22　3 种不同透风率栏杆的速度流线分布情况

由升力和力矩的时程数据知，MATLAB 程序根据最小二乘法原理识别颤振导数，计算结果见表5.12 至表5.14。

表5.12　大透风率栏杆（透风率为59.8%）颤振导数数值模拟计算结果

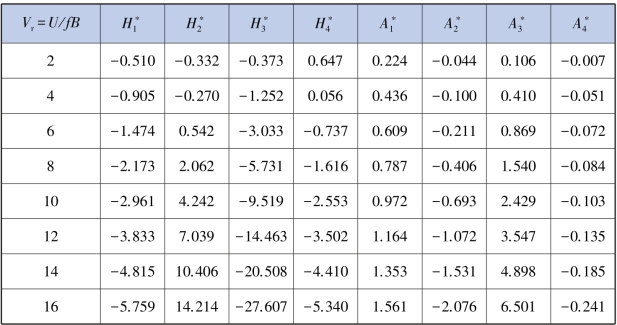
表5.13　中透风率栏杆（透风率为45.8%）颤振导数数值模拟计算结果

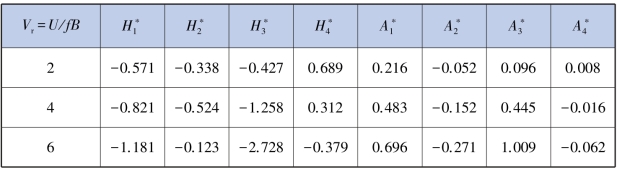
续表

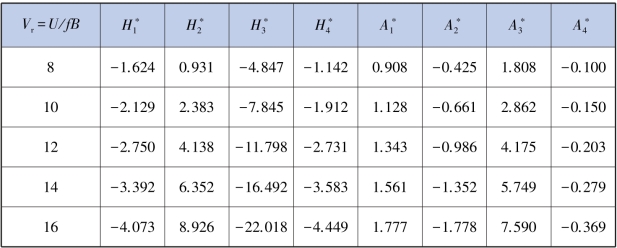
表5.14　小透风率栏杆（透风率为35.6%）颤振导数数值模拟计算结果

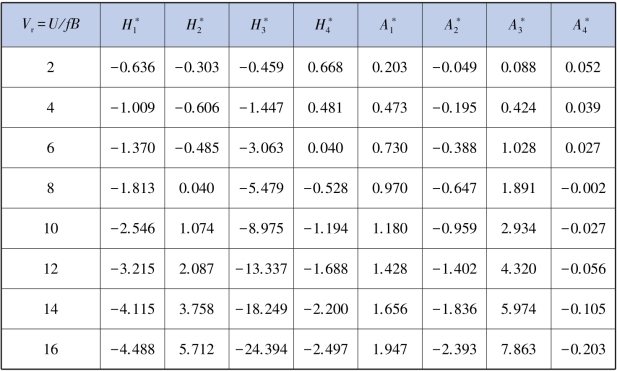
将3 种不同透风率栏杆模型颤振导数数值模拟计算结果进行对比，对比结果如图5.23所示。

从图5.23 中的对比可以看出，栏杆透风率的改变对颤振导数结果存在较大的影响，虽然不改变整体的变化趋势，但是数值的大小存在差异。 当折算风速Vr 较小时，不同透风率栏杆的颤振导数值较为接近，随着折算风速的增大，3 条曲线的差异越来越大，即在折算风速较大时，不同透风率栏杆颤振导数值差异较大。 这些结论与风洞试验得到的结论吻合。

采用SCANLAN 二维颤振临界风速计算方法，将数值计算得到的颤振导数计算结果代入式（5.57）和式（5.58），可得到实部方程（一元四次方程）和虚部方程（一元三次方程），由MATLAB 程序计算得到两个方程的理论解，并根据图解法绘制求解过程，如图5.24 所示。

根据式（5.61）求解颤振临界风速，求解过程及结果见表5.15。

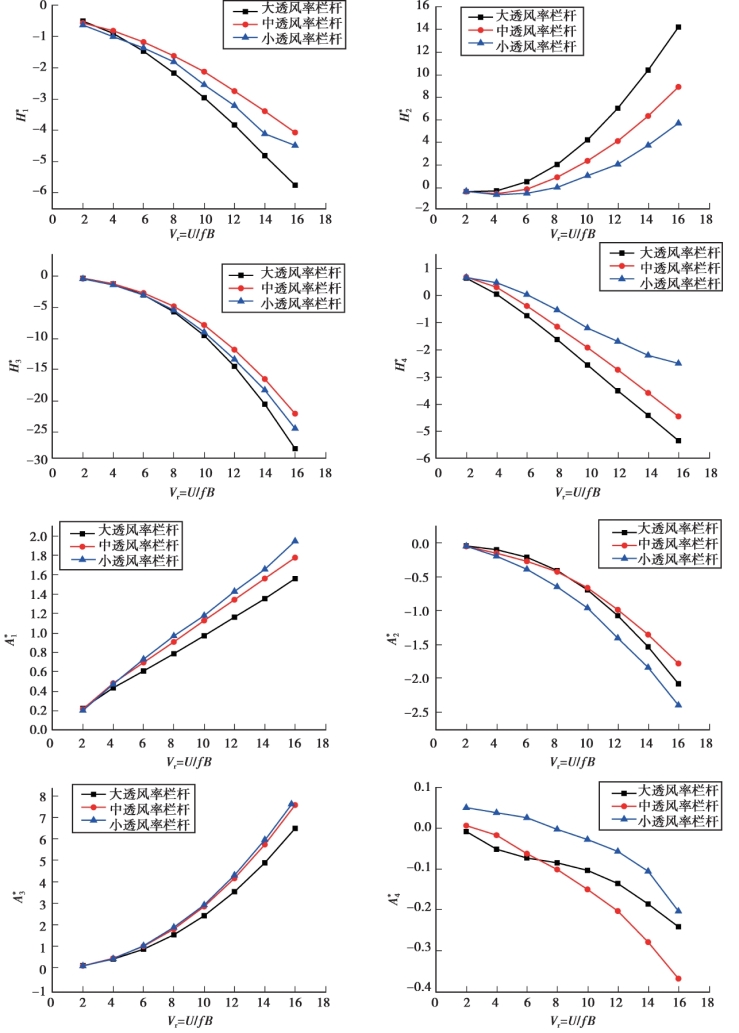
图5.23　3 种栏杆模型颤振导数的识别结果

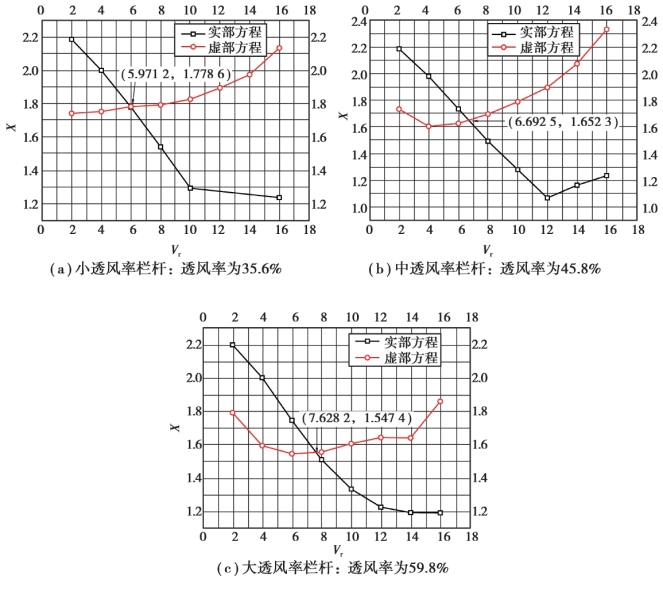
图5.24　图解法求解寸滩长江大桥（3 种栏杆形式）颤振临界风速

表5.15　主梁断面（3 种栏杆形式）颤振临界风速计算

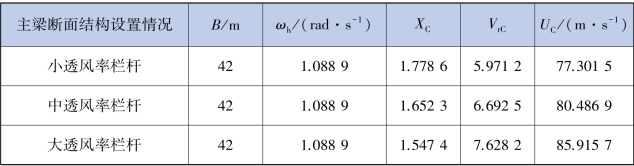
通过颤振导数的对比可知，栏杆的透风率大小对颤振导数的影响较大，本节通过计算不同透风率栏杆的颤振临界风速，得到具体的结论：栏杆透风率可显著影响颤振临界风速，透风率越大颤振临界风速值越大，故在进行主梁栏杆设计时，可以在实际条件允许的范围内尽可能地采取透风率较大的栏杆形式。

2）导流板对颤振性能的影响

在中透风率栏杆主梁节段模型的基础上增加导流板，探索导流板对颤振性能的影响，模型示意图和导流板尺寸如图5.25 所示。

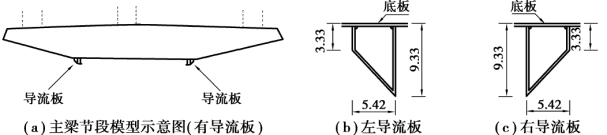
图5.25　主梁节段模型及导流板尺寸（单位：mm）

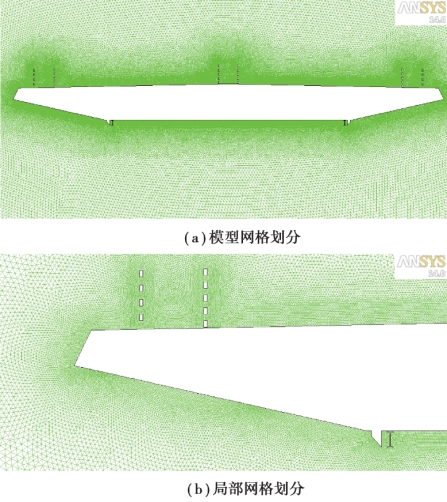
根据图5.25 划分网格，得到网格的总数为224 094，其中刚性边界层网格数为166 836，动网格数为35 458，静止网格数为21 800。 具体网格划分情况如图5.26 所示。

(www.daowen.com)

图5.26　主梁节段模型（有导流板）网格划分情况

对寸滩主梁节段模型（有导流板）速度流线分布进行考察，并与无导流板的模型进行对比，以风速取值32 m／s 为例，如图5.27 所示。

由升力和力矩的时程数据知，MATLAB 程序根据最小二乘法原理识别颤振导数，计算结果见表5.16。

表5.16　主梁节段模型（有导流板）颤振导数识别结果

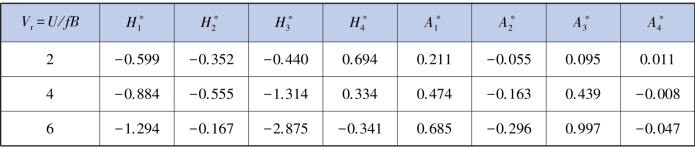
续表

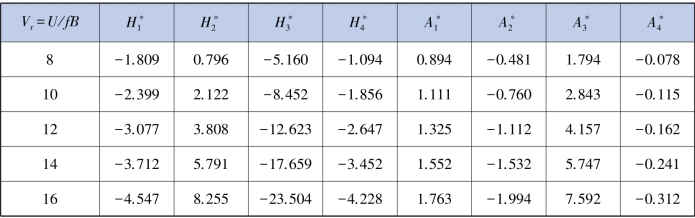
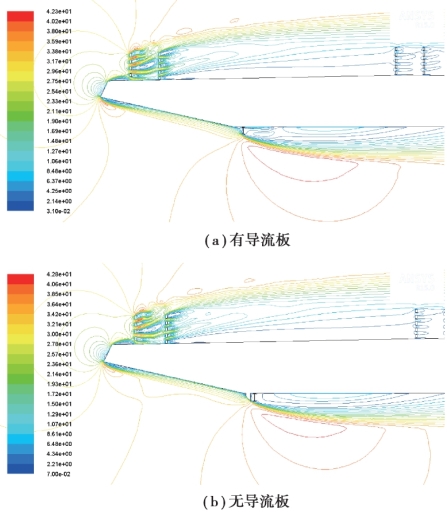
图5.27　主梁节段模型（有导流板和无导流板）速度流线分布

分别将有导流板模型和无导流板模型的颤振导数数值模拟计算结果进行对比，对比结果如图5.28 所示。

采用SCANLAN 二维颤振临界风速计算方法，将数值计算得到的颤振导数计算结果代入式（5.57）和式（5.58），可得到实部方程（一元四次方程）和虚部方程（一元三次方程）。 由MATLAB 程序计算得到两个方程的理论解，并根据图解法绘制求解过程，如图5.29 所示。

根据式（5.61）求解颤振临界风速，求解过程及结果见表5.17。

图5.28　主梁节段模型（有导流板和无导流板）颤振导数对比

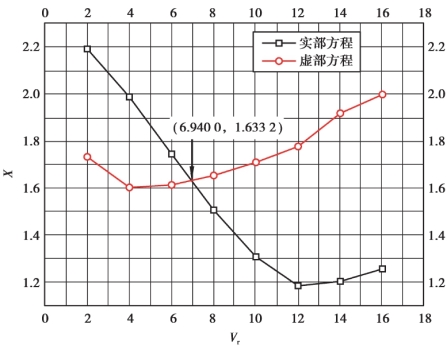
图5.29　图解法求解寸滩长江大桥（有导流板）颤振临界风速

表5.17　主梁断面（有导流板）颤振临界风速计算

从颤振导数的结果对比和颤振临界风速的结果对比均可看出，有导流板和无导流板对颤振性能存在一定的影响，添加导流板可以改变主梁断面的颤振稳定性，提高颤振临界风速，故在大跨悬索桥的设计中导流板的添置必不可少。

3）结果验证

分别对上述设置有3 种透风率栏杆的主梁模型，比较其数值模拟结果与风洞试验结果，主梁节段模型颤振导数的研究通过改变栏杆的透风率分为以下3 种情况：

①大透风率栏杆：透风率为59.8%。

②中透风率栏杆：透风率为45.8%。

③小透风率栏杆：透风率为35.6%。

图5.30 至图5.32 中给出了3 种透风率栏杆的颤振导数在风洞试验中得到的结果及数值计算结果，并进行了对比分析。

对颤振临界风速的研究，首先在节段模型风洞试验中采用直接测量的方法得到了颤振临界风速的大小，同时在数值模拟计算得到颤振导数之后，又采用SCANLAN 二维颤振临界风速计算的方法得到了颤振临界风速的大小，将两者得到的结果进行对比，见表5.18。

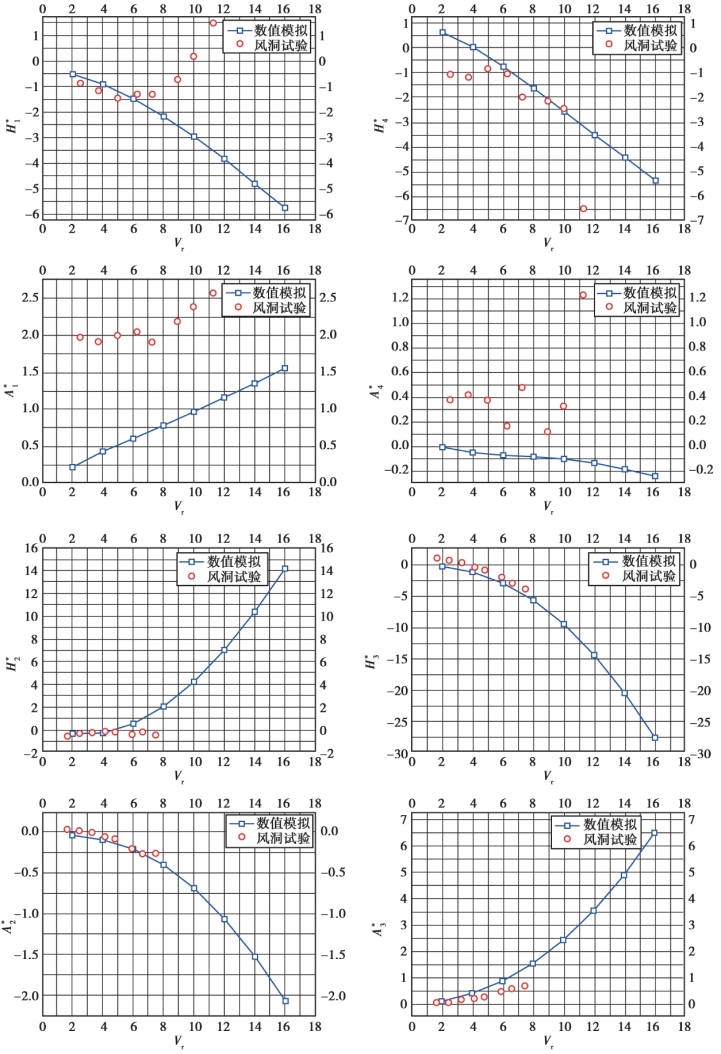
图5.30　节段模型（大透风率栏杆）颤振导数风洞试验结果与数值计算结果对比

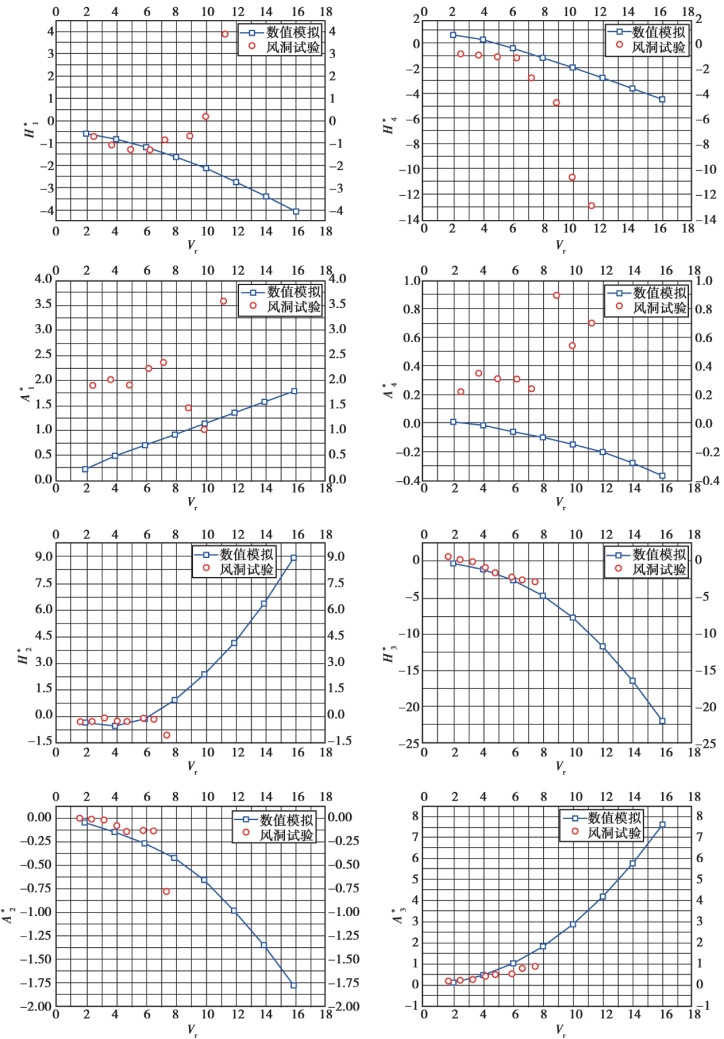
图5.31　节段模型（中透风率栏杆）颤振导数风洞试验结果与数值计算结果对比

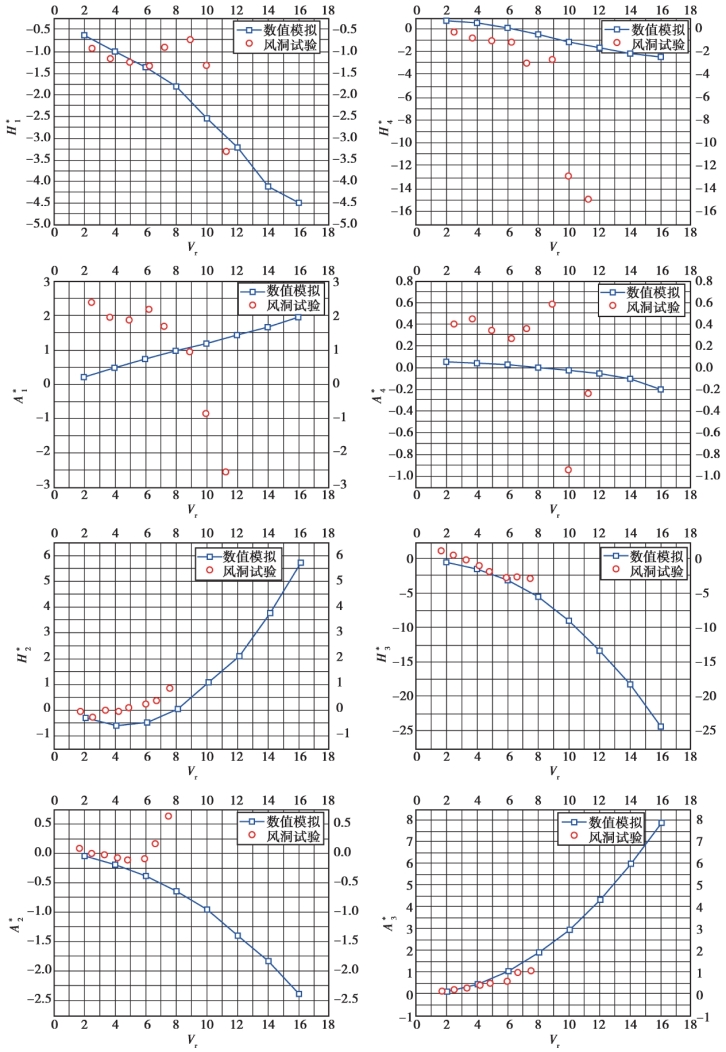
图5.32　节段模型（小透风率栏杆）颤振导数风洞试验结果与数值计算结果对比

表5.18　颤振临界风速风洞试验测量结果与数值模拟计算结果对比

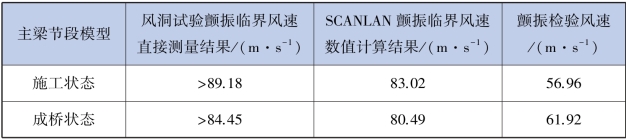
对两种方法得到的颤振临界风速值进行对比，两者结果的差距在可接受的范围之内，同时，两种方法得到的结果均大于颤振检验风速，说明本桥的颤振稳定性满足要求。 实测数据与模拟数据相差不大，表明采用数值模拟计算的方法可以预估桥梁的颤振临界风速，其结果可以用于桥梁的初步设计，具有一定的工程意义。