模型在强迫振动下分别做单自由度的竖弯运动和单自由度的扭转运动，首先迭代100步（2T）使残差稳定，然后再迭代300 步（6T），采集后300 步（6T）的升力系数和力矩系数的数据。

以风速U＝12 m／s 为例，其升力系数和力矩系数的时程曲线，如图5.10 所示。

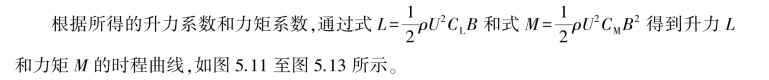
这里分别考察模型在单自由度的竖弯运动和单自由度的扭转运动时的压力分布变化情况，在提取结果时，将一个周期T 分为4 个时间节点T／4，2T／4，3T／4，T 分别进行考察，从而了解在一个周期内的压力分布变化情况。

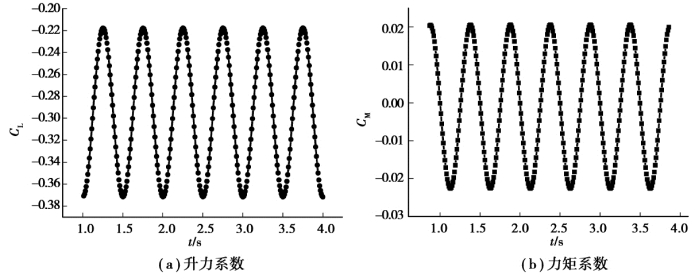
图5.10　竖弯运动气动力系数时程曲线

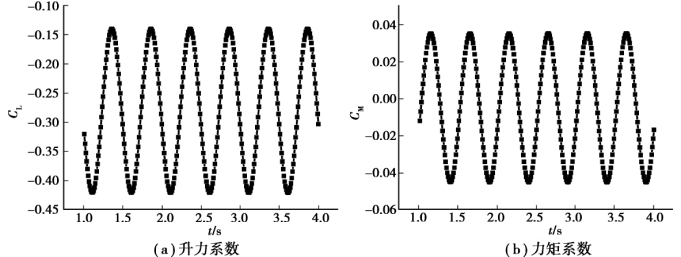
图5.11　扭转运动气动力系数时程曲线

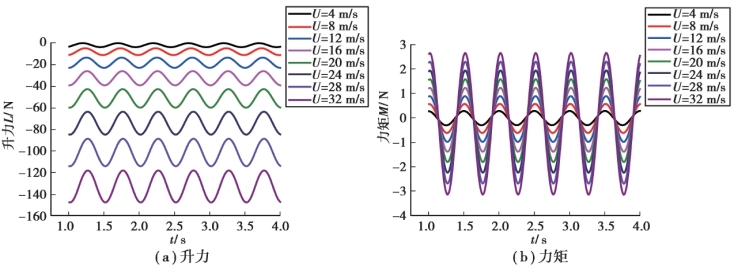
图5.12　模型在各级风速下做纯竖弯强迫振动的气动力时程曲线

以风速U＝12 m／s 为例，其压力等高线分布如图5.14 和图5.15 所示。

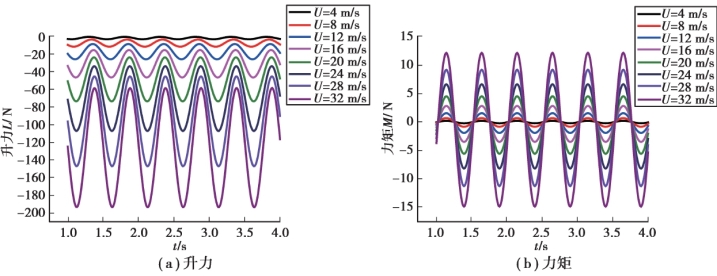
图5.13　模型在各级风速下做纯扭转强迫振动的气动力时程曲线

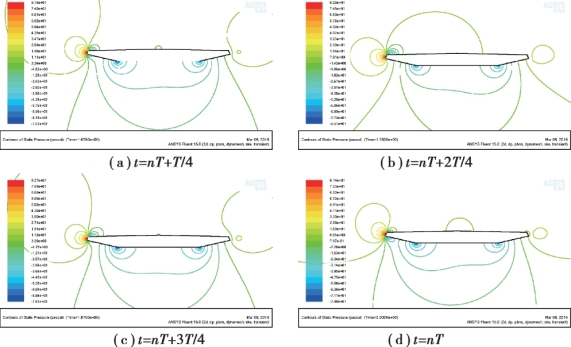
图5.14　模型做纯竖弯运动的压力等高线分布

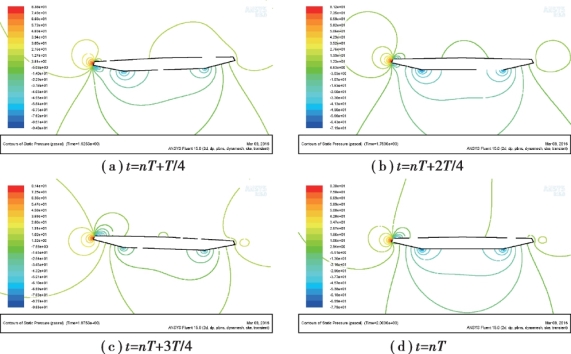
图5.15　模型做纯扭转运动的压力等高线分布

这里分别考察模型在单自由度的竖弯运动和单自由度的扭转运动时的速度流场分布变化情况，在提取结果时，将一个周期T 分为4 个时间节点T／4，2T／4，3T／4，T 分别进行考察，从而了解在一个周期内的速度流场的变化情况。

以风速U＝12 m／s 为例，其速度流场云图分布如图5.16 和图5.17 所示。(www.daowen.com)

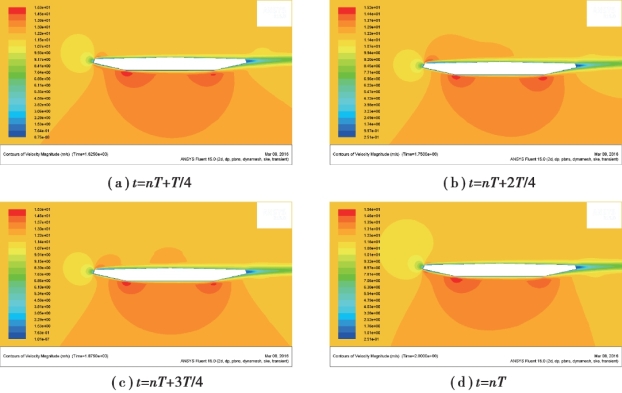
图5.16　模型做纯竖弯运动的速度流场分布

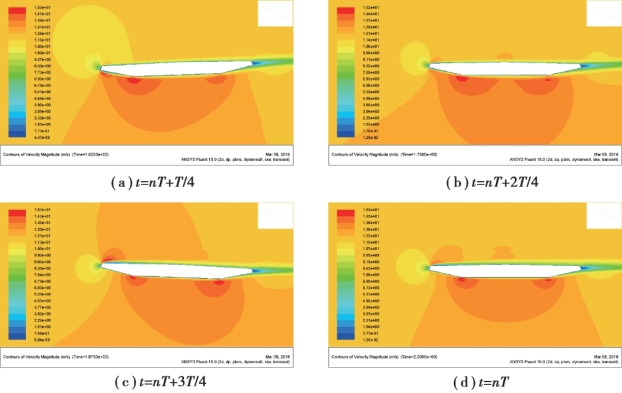
图5.17　模型做纯扭转运动的速度流场分布

由升力和力矩的时程数据知，MATLAB 程序根据最小二乘法原理识别颤振导数，计算结果见表5.10。

表5.10　节段模型颤振导数数值模拟计算结果

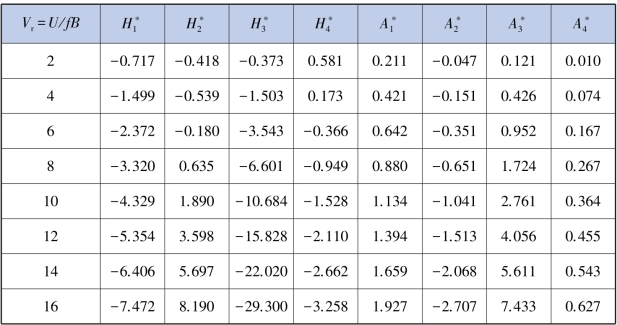
将主梁节段模型颤振导数数值模拟计算结果与理想平板颤振导数数值模拟计算结果进行对比，对比结果如图5.18 所示。

采用SCANLAN 二维颤振临界风速计算方法，将数值计算得到的颤振导数计算结果代入式（5.57）和式（5.58），可得到实部方程（一元四次方程）和虚部方程（一元三次方程），由MATLAB 程序计算得到两个方程的理论解，并依据图解法绘制求解过程，如图5.19 所示。

同时依据式（5.61）求解颤振临界风速，求解过程及结果见表5.11。

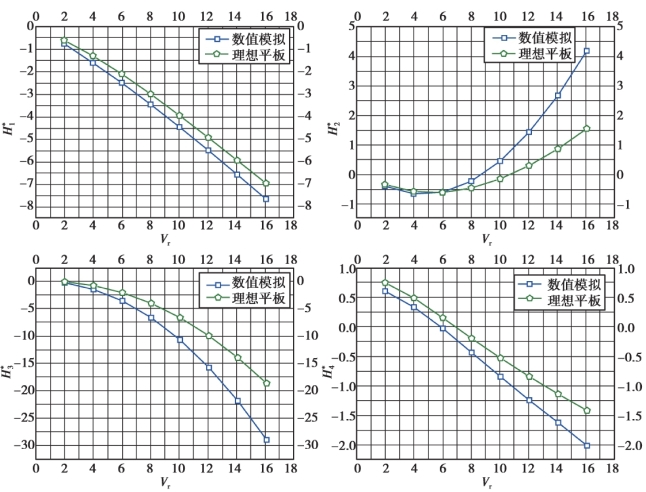
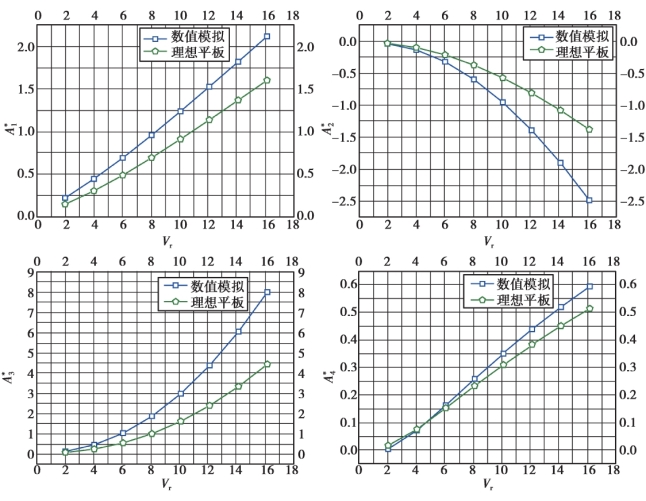
图5.18　寸滩节段模型颤振导数的识别结果

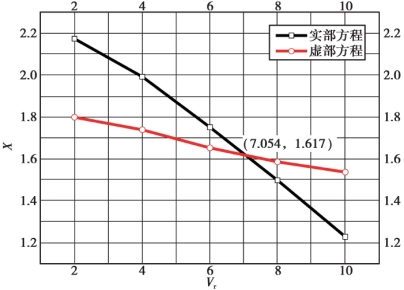
图5.19　图解法求解寸滩长江大桥（无附属结构）颤振临界风速

表5.11　寸滩长江大桥（无附属结构）颤振临界风速计算