进行颤振导数识别试验时，分别考虑施工状态和成桥状态的影响，通过试验得到识别其颤振导数值。

1）成桥状态的工况设置

在进行成桥状态的颤振导数识别试验时，通过变换人行道栏杆的形式，分别考虑了栏杆不同透风率的影响，从而探索模型气动外形的改变对颤振导数的影响情况，图5.1 给出了主梁标准断面的详细尺寸及栏杆的几种布置形式。

在试验中防撞护栏的位置和形式保持不变，通过改变栏杆的形式分别考虑了3 种试验工况：大透风率、中透风率和小透风率。

在颤振导数试验中，对3 种人行道栏杆的透风率设置形式下，分别进行均匀流场中0°风攻角的颤振导数试验，试验风速为0，4，6，8，10，12，14，16，18 m／s，每个风速下均试验6 次，取颤振导数识别结果的平均值作为最终值。

2）施工状态的工况设置

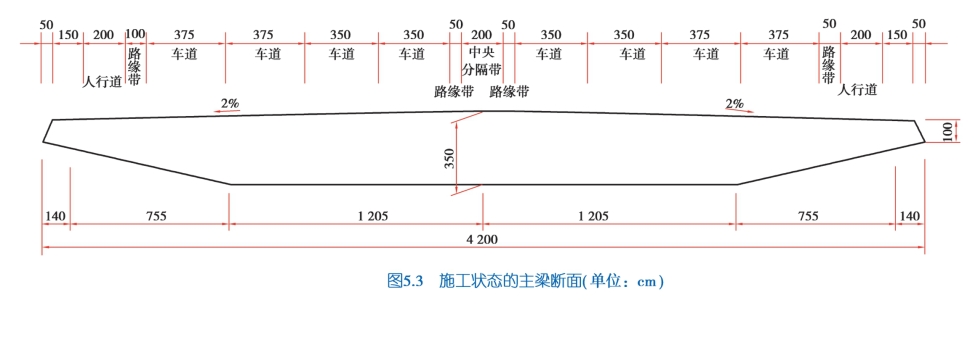
在进行施工状态的颤振导数识别试验时，主梁断面的防撞护栏、人行道栏杆以及检修导轨均未安装，如图5.3 所示。

进行均匀流场中0°风攻角的颤振导数试验，试验风速为0，4，6，8，10，12，14，16，18 m／s，每个风速下均试验6 次，取颤振导数识别结果的平均值作为最终值。

3）颤振导数识别试验工况

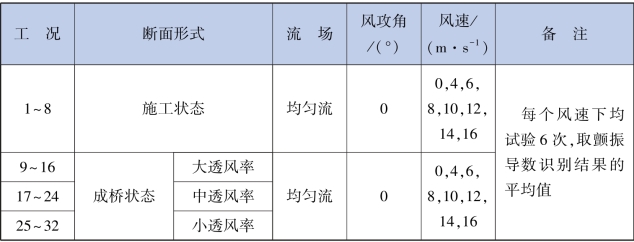
综上所述，所有试验工况的设置见表5.3。

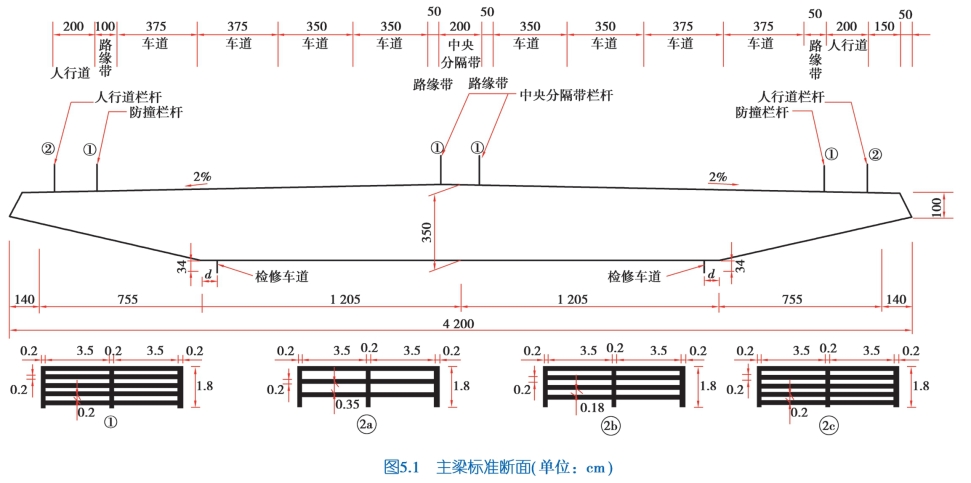
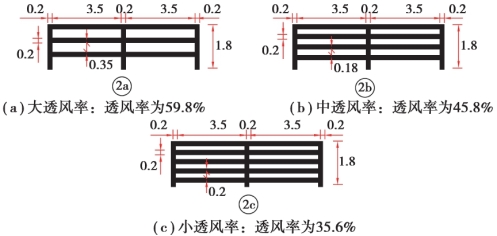
图5.2　不同人行道栏杆形式的透风率设置情况（单位：cm）

表5.3　颤振导数识别试验工况

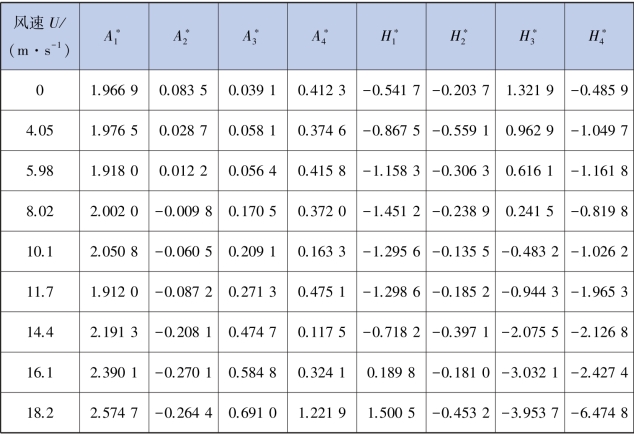
由施工状态颤振导数识别试验得到的数据，应用MATLAB 程序根据最小二乘法原理识别颤振导数，将6 次试验得到的结果取平均值可得到最终的颤振导数识别结果，见表5.4。

表5.4　施工状态颤振导数识别结果

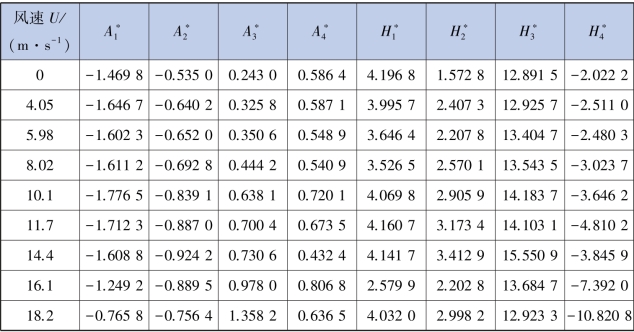
注：表中数据均为6 次试验结果数据处理之后的平均值。
根据数据fh ＝2.308； fα ＝3.479；B ＝0.7 m，可得相应的折算风速Vr ＝U／fB，整理数据后可得到颤振导数曲线。(www.daowen.com)

由成桥状态（大透风率）颤振导数识别试验得到的数据，应用MATLAB 程序根据最小二乘法原理识别颤振导数，将6 次试验的结果取平均值可得到最终的颤振导数识别结果，见表5.5。

表5.5　成桥状态（大透风率）颤振导数识别结果

注：表中数据均为6 次试验结果数据处理之后的平均值。
根据数据fh ＝2.308； fα ＝3.479；B ＝0.7 m，可得相应的折算风速Vr ＝U／fB，整理数据后可得到颤振导数曲线。

由成桥状态（中透风率）颤振导数识别试验得到的数据，经数据处理可得到最终的颤振导数识别结果，见表5.6。

表5.6　成桥状态（中透风率）颤振导数识别结果

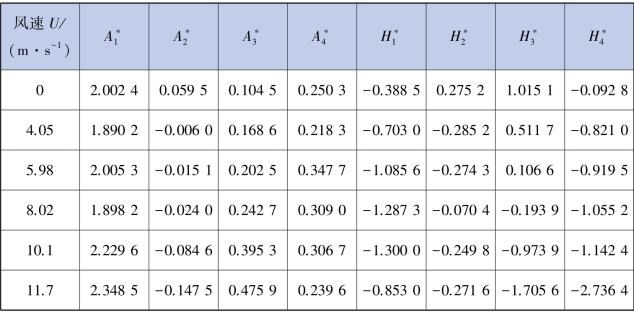
续表

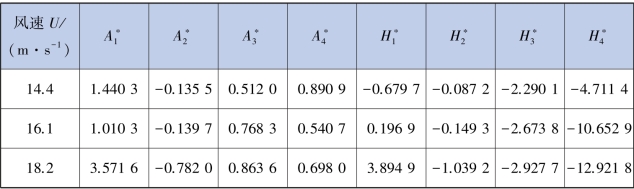
注：表中数据均为6 次试验结果数据处理之后的平均值。
根据数据fh ＝2.308； fα ＝3.479；B ＝0.7 m，可得相应的折算风速Vr ＝U／fB，整理数据后可得到颤振导数曲线。

由成桥状态（小透风率）颤振导数识别试验得到的数据，经数据处理可得最终的颤振导数识别结果，见表5.7。

表5.7　成桥状态（小透风率）颤振导数识别结果

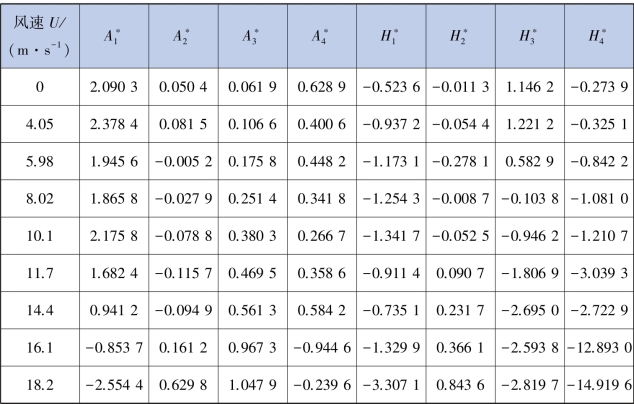
注：表中数据均为6 次试验结果数据处理之后的平均值。
根据数据fh ＝2.308； fα ＝3.479；B ＝0.7 m，可得相应的折算风速Vr ＝U／fB，整理数据后可得到颤振导数曲线。

这里分别在成桥状态设置3 种不同透风率的栏杆形式，探索气动外形的改变对颤振导数的影响情况，从图5.4 中的对比结果可以看出，根据风洞试验中主梁节段模型的自由振动来识别颤振导数的方法具有较大的不稳定性，本试验通过每级风速下进行6 次重复试验取平均值的方法来消除不稳定的影响，但依然存在较大的误差。 通过试验结果的比较可以看出，成桥状态下设置3 种不同透风率的栏杆，对8 个颤振导数的整体变化趋势没有影响，即3种不同透风率的栏杆其颤振导数的变化趋势保持一致，只是数值大小存在差异。 同时还能发现，当折算风速Vr 较小时，不同透风率栏杆的颤振导数值较为接近，但随着折算风速的增大，3 条曲线的差异越来越大，即在折算风速较大时，不同透风率栏杆的颤振导数值差异较大。

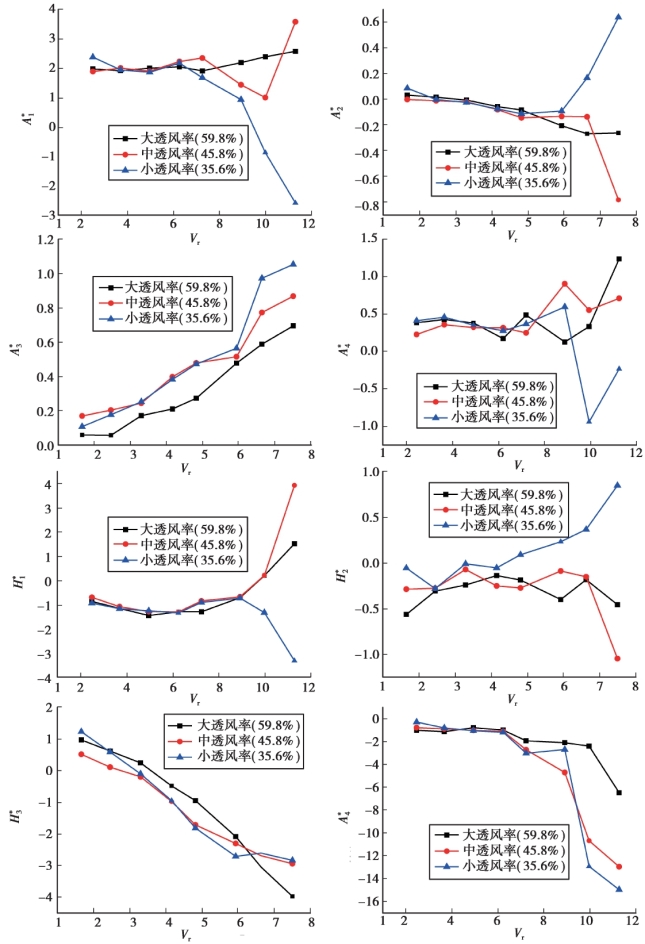
图5.4　成桥状态的颤振导数与折算风速的关系曲线