本书中数值模拟计算采用的方法是分状态强迫振动识别法，即分别让模型在流场中做单自由度的竖弯振动和单自由度的扭转振动，再根据获得的气动力时程数据对两自由度的8个颤振导数进行识别。

首先让模型做单自由度的竖弯振动，可知α（t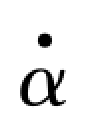）＝（t）＝0 时，运动方程为：

则线速度为：

然后让模型做单自由度的扭转振动，可知h（t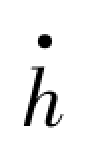）＝（t）＝0 时，运动方程为：

则角速度为：

用Scanlan 颤振临界风速计算方法来对主梁断面的颤振临界风速值进行估算的理论推导如下。

主梁断面的运动方程为：

式中　m，Im——模型单位长度的等效质量和等效质量矩；

ξh，ξα——竖弯振动和扭转振动的阻尼比；

h，α——竖弯振动和扭转振动的位移；

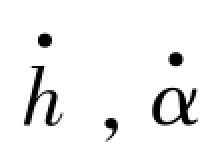——竖弯振动和扭转振动的速度；(www.daowen.com)

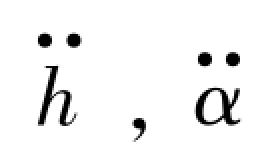——竖弯振动和扭转振动的加速度。

将式（5.1）带入式（5.53），同时引入无量纲时间s＝tU／B，得到无量纲化的运动方程：

将其代入式（5.54），则：

定义未知函数X ＝ω／ωh，代入式（5.56），得：

方程有解的条件是系数行列式为零，根据系数行列式为零整理得到X 的四次多项式，进一步整理得到实部和虚部两个方程如下：

式中：

选择不同的K 值以及与其对应的8 个颤振导数值，可解得实部方程中的XR（K）和虚部方程中的XI（K），在一张图中绘制XR⁃K 和XI⁃K 曲线，可以得到两条曲线的交点（KC，XC），这个交点就是对应的临界状态。

对应的圆频率为：

颤振临界风速为：

计算时采用的横坐标是与K 值对应的折算风速Vr，由VR⁃Vr 和VI⁃Vr 两条曲线的交点（VrC，XC）来确定临界状态，对应的颤振临界风速计算公式为：