式中　h，α——竖弯和扭转两个方向上的振幅；

U——来流风速；

B——全桥宽；

b——半桥宽；

K——无量纲频率；

k——无量纲折算频率；

ω——振动圆频率；

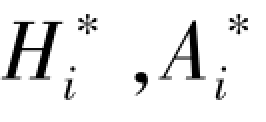（i＝1，2，3，4）——无量纲颤振导数，是来流折算频率k 或折算速度Vr ＝U／fB ＝π／k 的函数，颤振导数主要取决于模型外形，其中f 为模型振动频率。

假设均匀流场中有理想平板，宽度为B，且质心和转动中心均位于截面的中心，在某种扰动下，理想平板产生轻微的非定常运动，那么这种运动只有竖向平动和扭转运动两个自由度。 进一步假设理想平板两个方向的运动均为简谐运动，运动方程如下：

Theodorsen 等经过推导得到理想平板气动力的表达式为：

式中　L——单位长度的升力；

M——单位长度的扭矩；(www.daowen.com)

ρ——空气密度；

b——薄平板半宽，板宽B ＝2b；

U——空气来流速度；

h——截面竖向位移；

α——截面扭转角；

k——无量纲折算频率，k ＝bω／U，ω 为振动圆频率；

C（k）——Theodorsen 循环函数，得到的近似表达式为：

为了得到理想平板颤振导数的理论解，需要将所得到的平板气动力表达式（5.3）写成颤振导数定义式（5.1）的形式，然后进行对比就可得到理想平板的颤振导数。 要达到上述目的，需采用简谐振动的复指数形式：

将表达式中的理想平板半宽b 用B／2 替换，最终得到理想平板颤振导数的Theodorsen理论解表达式如下：

从表达式可以看出，理想平板颤振导数Theodorsen 理论解只与无量纲折算频率k 有关。