为了研究桥面粗糙度对宽体式扁平钢箱梁涡振性能的影响，对3 种不同桥面粗糙度下的主梁进行了涡振试验，在涡振试验中选用未加砂纸的主梁模拟A 级桥面粗糙度，120 目砂纸模拟B 级桥面粗糙度，80 目砂纸模拟C 级桥面粗糙度，B 级桥面粗糙度涡振试验如图4.21所示。

图4.21　B 级桥面粗糙度涡振试验

根据表3.5 中的竖弯频率、竖弯阻尼比、扭转频率、扭转阻尼比计算出涡振试验中竖向风速比和扭转风速比分别为4.72 和4.41。 基于缩尺比和计算的风速比便可得到实桥风速和实桥涡振响应间的关系。 换算至实桥风速为0 ～35.0 m／s，控制风速基本步长约1.0 m／s，试验中根据模型的振动情况适当细化步长。 涡振试验结果显示3 种桥面粗糙度在－3°，－5°风攻角时都没有明显的涡振区，表明负风攻角下主梁气动特性很好。 3 种桥面粗糙度在＋5°，＋3°，0°时的竖向涡振响应如图4.22 所示。

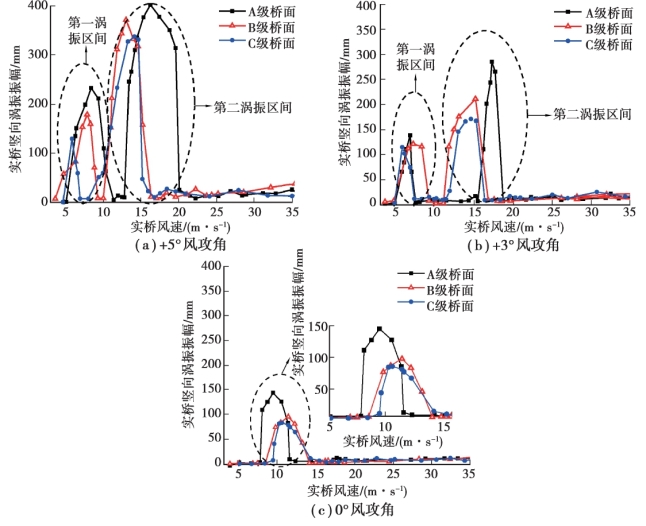
图4.22　主梁竖向涡振响应

由图4.22 可知：

①竖向涡振振幅最大值随桥面粗糙度的增加不断降低。 如＋5°风攻角时，A，B，C3 级桥面粗糙度下的最大竖向振幅分别为398.46，369.13，335.18 mm。

②风攻角为0°，＋3°和＋5°时，从A 级到B 级最大竖向振幅降低幅度分别为7.36%，25.8%和32.63%，从B 级到C 级最大竖向振幅降低幅度分别为9.20%，14.39%和17.53%，表明桥面粗糙度对主梁竖向振幅降低幅度随风攻角的减小而增大，即风攻角较小时对桥面粗糙度变化更敏感。

③相同桥面粗糙度下，最大竖向振幅随风攻角减小而降低。 如A 级桥面在风攻角为＋5°，＋3°和0°时的最大竖向振幅分别为398.46，283.99，145.26 mm。

④＋5°和＋3°风攻角时存在两个涡振区，而0°风攻角时只有一个涡振区。 由于本书研究的桥面较宽，大攻角下出现了气流再次附着，产生了两个涡振区。

三种桥面粗糙度在＋5°，＋3°，0°时的扭转涡振响应，如图4.23 所示。(www.daowen.com)

由图4.23 可知，不同桥面粗糙度下扭转角度变化规律大部分与竖向涡振振幅的变化规律相似，具体如下：

①扭转角度最大值随桥面粗糙度的增加而减小。

②桥面粗糙度相同时，最大扭转角度随风攻角减小而降低。

③风攻角为＋3°，＋5°时同样存在两个涡振区，且风攻角为0°时只有一个涡振区。

其不同之处在于：

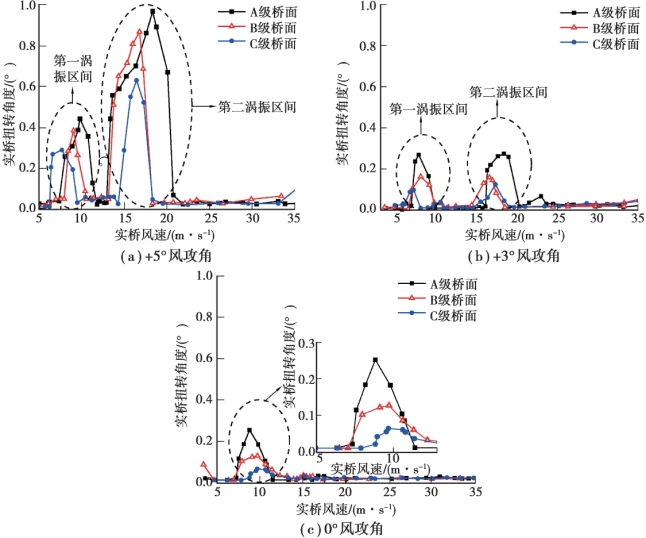
图4.23　主梁扭转涡振响应

①风攻角为0°，＋3°和＋5°时，从A 级到B 级最大扭转角度降低幅度分别为49.8%，41.76%和10.27%；从B 级到C 级最大扭转角度降低幅度分别为50.79%，22.01%和27.91%。其降低幅度大于在同样风攻角下，桥面粗糙度发生同样变化的竖向涡振振幅，表明扭转角度更容易受桥面粗糙度变化的影响。 本书研究的主梁断面的宽高比为12，比一般扁平钢箱梁宽高比大，更接近流线型结构，因此桥面粗糙度发生相同变化时，扭转涡振响应变化幅度大于竖向扭转涡振响应变化幅度。

②风攻角为0°，＋3°和＋5°时，竖向涡振最大值有明显变化，而扭转涡振响应在＋5°时与0°和＋3°相差较大，但是0°，＋3°之间相差不大。

③在风攻角为＋5°时，3 种桥面粗糙度下扭转第二涡振区间最大值远大于第一涡振区间；在风攻角为＋3°时，3 种桥面粗糙度下第一、第二涡振区间最大值基本相同。

④竖向涡振区间随桥面粗糙度变化规律不明显，而扭转涡振区间随桥面粗糙度增大而减小。 ＋5°风攻角时第二扭转涡振区间减小幅度最为明显，A，B，C 3 级桥面粗糙度的涡振区间分别为12.89～22.18 m／s、10.15～17.09 m／s 和8.17～16.80 m／s。