桥面粗糙度是引起桥上车辆竖向振动的主要激励源，也是影响桥上车辆安全的主要因素。 车辆行驶时会对桥面产生附加动荷载，这种动荷载会让桥面粗糙度变差，产生表面裂缝、车辙、滑移等病害。 桥面粗糙度变差不仅会影响桥梁的正常运营还会影响驾驶员及乘客的舒适度，因此，要及时对桥面进行维护，确保桥面粗糙度处于良好状态。

桥梁的桥面粗糙度模拟计算与路面粗糙度相同。 一般桥面的空间频率段分布为0.011～2.830 m－1，车速范围为10.0～40.0 m／s，时间频率范围为0.44～28.30 Hz。 将时间频率范围划分为200 份，采样频率为0.01 s。 通常情况下，钢箱梁桥梁桥面粗糙度为A 级，钢管混凝土拱桥桥面粗糙度有可能达到B 级，实际中基本不会出现C 级桥面粗糙度，但为了进行对比，研究主梁气动力及涡振性能随主梁的变化趋势，本书同样选取C 级桥面粗糙度进行研究。 通过MATLAB 利用重构的三维路面粗糙度编程模拟得到了A，B，C 3 种等级桥面粗糙度的变化范围，其结果见表4.2。

表4.2　桥面粗糙度的变化范围

桥面粗糙度的功率谱密度函数和标准功率谱密度函数通过傅里叶逆变换得到，相干性曲线通过相干函数得到。 以B 级桥面粗糙度为例具体说明，其结果如图4.14 所示。 图4.14（a）和图4.14（b）分别为桥面粗糙度三维图和路宽2 m 处沿桥面长度方向的粗糙度示意图，可以得出，B 级桥面粗糙度绝大部分为－0.020 ～＋0.020 m，且围绕零值附近均匀稳定波动，基本上可以反映桥面粗糙度的随机性和稳定性。 当车辆采用5 自由度以上模型时，每个车轮处均需输入桥面粗糙度，左右两侧车轮受激励是具有相同功率谱密度的随机信号，因此，需考虑左右两轮之间的相干性。 任意取两条桥面粗糙度曲线得到其相干函数曲线（本书中选取桥面宽度分别为3.0 m 和15.0 m 处沿长度方向的粗糙度），如图4.14（c）所示。 可以看出，当f＞5 Hz 时，模拟结果相差不大；当0＜f＜2.5 Hz 时，模拟结果下降斜率基本一致；当2.5＜f＜5.0 Hz 时，由于模拟结果的振动幅度过大存在一定的误差。 模拟的较好频率范围将汽车悬挂（车身）质量部分的固有频率1.0 ～2.0 Hz 和非悬挂（车轮）质量部分的固有频率10.0 ～16.0 Hz 包含在内，因此，模拟得到的结果可以反映真实桥面的粗糙度状况。

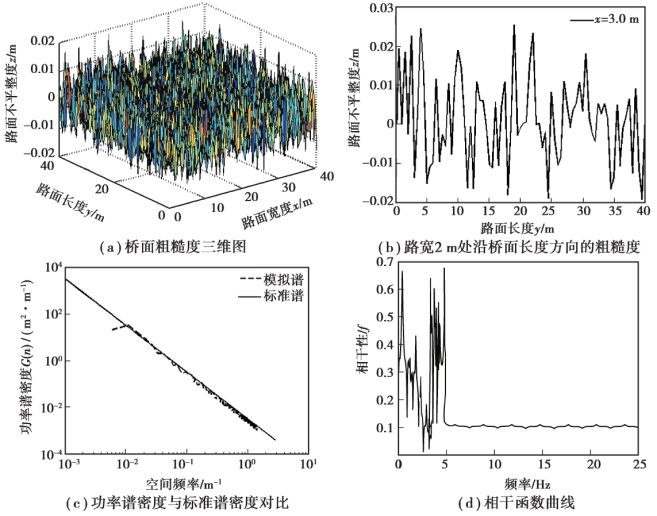
图4.14　B 级桥面粗糙度

节段模型风洞试验不仅要求模型与实桥在几何外形上相似，还要求二者之间的频率比和阻尼比一致。 试验中取节段模型几何缩尺比为1／60，模型长为2.1 m、宽为0.7 m、高为0.058 3 m。 根据桥面粗糙度的实际变化范围（表4.2）以及模型几何缩尺比可得试验中A，B，C3 种桥面粗糙度变化范围应分别为－0.083 ～＋0.083 mm、－0.500 ～＋0.500 mm、－0.666 ～＋0.666 mm。 A 级桥面粗糙度变化范围较小，不足0.100mm，考虑到制作节段模型桥面的木材表面有轻微的不平度，所以用未加砂纸的主梁模拟A 级桥面粗糙度。 B 级和C 级桥面粗糙度采用砂纸模拟，砂纸不平度变化范围具体量测方法为：对砂纸两边沿长度方向（总长2.1 m）用游标卡尺每隔75.0 mm 测量1 次，共56 个测点，记录其变化范围，每种砂纸测量3组。 大量的量测结果表明，120 目和80 目砂纸的平均变化范围的分别为－0.487 ～＋0.487 mm和－0.640～＋0.640 mm，与模拟结果相差不大。 因此，选用120 目砂纸模拟B 级桥面粗糙度，80 目砂纸模拟C 级桥面粗糙度。

三种桥面粗糙度下静力三分力系数试验，如图4.15 所示。 图4.16 为－12°～＋12°风攻角下，桥面粗糙度从A 级增大到C 级时静力三分力系数的变化情况。 其中CD 为阻力系数，CM为力矩系数，CL 为升力系数。

由图4.16 可知，在相同风攻角不同桥面粗糙度条件下：

①阻力系数CD 从大至小的顺序均为A，B，C 级桥面粗糙度，表明CD 随桥面粗糙度的增大而减小。

②力矩系数CM 的变化范围很小，基本不随桥面粗糙度的变化而变化。

③升力系数CL 在负风攻角范围内无明显变化，在正风攻角范围内随着桥面粗糙度增大而增大。 对比CD，CL，CM 随桥面粗糙度的变化幅度可以看出，CD 的变化幅度最大，CM 最小，表明桥面粗糙度对静力三分力系数影响的大小依次为CD，CL，CM。

粗糙度对三分力系数CD，CL 和CM 随风攻角的变化趋势影响较小，A，B，C3 级桥面下相同的三分力系数随风攻角的变化趋势基本一致，具体如下：

(www.daowen.com)

图4.15　三种桥面粗糙度下静力三分力系数试验

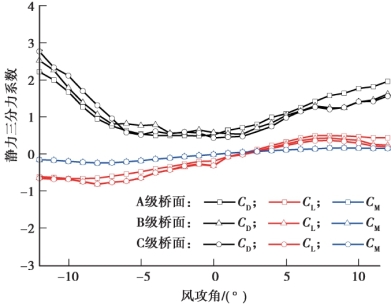
图4.16　桥面粗糙度对静力三分力系数的影响

①阻力系数CD 在风攻角为－7°～＋12°时随风攻角增大而增大，且风攻角为－7°～－2°时曲线形状明显陡于－2°～＋12°时的曲线，即在－7°～－2°阶段的增大速率远大于－2°～＋12°阶段的增大速率。 而在－12°～－7°时，CD 随风攻角增大而减小，且减小速率与风攻角－7°～－2°时的增加速率基本相同。

②力矩系数CM 的变化最大的为C 级桥面，范围为－0.166 ～0.165 m，表明CM 基本不随风攻角的变化而变化。

③升力系数CL 在－12°～－9°上基本不变，在－9°～＋12°时随风攻角增大而增大，且曲线越来越缓，表明CL 的增加速率随风攻角增大而减缓。

为了便于观察主梁断面附近流线轮廓、速度分布和压强分布变化的情况，选取风攻角为－12°，－8°，＋12°这3 种工况进行模拟。 应用roughness height 单元模拟桥面粗糙度，近似地将砂纸平均砂粒高度视为桥面粗糙度的厚度。 在划分边界条件时，将模型上表面（包括风嘴）单独设一个壁面wall 边界，求解时，将其roughness height 设为0.97 mm或1.28 mm 即实现了对B 级（80 目砂纸）和C 级（120 目砂纸）桥面粗糙度的模拟。 在网格划分方面，为了更好地分辨桥面的不平度颗粒，断面上表面划分边界层网格，第一层网格高度为0.05 mm。 将主梁附近划分为8 个区域，分别计算出每个区域内网格节点的平均压强和速度值作为比较依据。图4.17 和图4.18 为不同桥面粗糙度下主梁附近流线轮廓及速度分布。

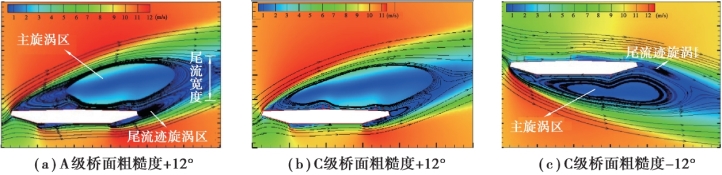
图4.17　主梁附近流线轮廓及速度分布（单位：m／s）

图4.18　主梁断面附近压强分布（单位：Pa）

由图4.17（a）、（b）可知，风攻角为＋12°时桥面上方的主旋涡区随桥面粗糙度增大而增加，主梁下游尾迹区的旋涡缩小，尾流宽度变窄。 由图4.18（a）、（b）、（c）可知，背风侧负压区的范围、压强绝对值均随桥面粗糙度增大而减小，通过计算，得到迎、背风侧压力差由30.42 Pa减小到20.18 Pa，从而导致阻力系数减小。

由图4.17（a）、（b）可知，当来流为正风攻角时，桥面粗糙度的增大使得上表面风速增大，通过计算，得到上表面风速由4.81 m／s 增大到5.95 m／s。 由图4.18（a）、（b）、（c）可知，上侧负压区压强绝对值增大，上侧负压区压强绝对值由20.36 Pa 增大到24.58 Pa，上下压力差增大，最终导致升力系数增大；桥面粗糙度主要影响的是断面上方的流场分布，当来流为负风攻角时，图4.17（c）是风攻角为－12°时主梁附近流线轮廓及速度分布，主旋涡及尾迹区旋涡均位于断面下方，受桥面粗糙度的影响微乎其微，因此升力系数的变化并不明显。 力矩系数由左上、右下侧压强差及右上、左下侧压强差决定。 通过计算得出，图4.18（a）、（b）、（c）中，左上和右下侧压强差分别为16.41，16.40，16.41 Pa；右上和左下侧压强差分别为17.32，17.33，17.31 Pa，压强差值的变化范围不大。 因此，力矩系数基本不受桥面粗糙度变化的影响。