路面粗糙度是对路面评价的一个关键因素。 车辆的振动是路面的不平度引起的，在人⁃车⁃路、风⁃车⁃桥系统中进行研究时，路面粗糙度都是振动系统的激励源，是影响整个系统振动情况的重要因素。 路面粗糙度早期主要是通过实际测量获得，随着数值模拟的发展，研究人员开始在理论测试基础上进行路面的建模和模拟，提出了多种时域和频域的路面模型。在路面粗糙度数值模拟中，最初是对二维路面粗糙度模拟，模型分为四大类。 研究车⁃路系统振动情况初期，用的是车辆独轮车模型、半车模型。 独轮车和半车模型中，输入的是与路面方向垂直的二维路面不平度。 随着研究的不断深入，车辆模型的自由度越来越多，有整车4 自由度模型、5 自由度模型、二轴13 自由度模型、三轴17 自由度模型、三轴21 自由度模型。 为了研究冰、雪、雨、风引起车辆侧翻、侧滑以及考虑驾驶员行为和乘客舒适度的车⁃桥、车⁃路耦合振动，建立4 自由度以上的模型能够得到更精确的结果，需要在每个车轮下面都输入不平度激励，而二维路面粗糙度模型不能很好地解决此类问题，因此许多学者进行了三维路面粗糙度的推导和重构。 目前，用于三维路面粗糙度的推导与重构的方法有：将一维路面功率谱扩展成二维推导三维路面粗糙度；构建路面高程迭代函数系统，用随机三维分形插值的方法对原始测量的路面数据进行插值得到三维路面粗糙度；用改进的谐波合成法将路面粗糙度拓展到三维空间内的路面粗糙度；通过三角级数法，计算出路面粗糙度特性，推导出三维路面随机位移的表达式。

路面粗糙度位移功率谱密度的拟合表达式为：

式中　Gq（n）——路面粗糙度功率谱密度，m－1，其中n 为空间频率；

n0——参考空间频率，m－1，n0 ＝0.1；

Gq（n0）——路面粗糙度系数，m2／m－1；

w——频率指数，w ＝2。

车辆行驶过程中轮胎受到的激励频率与空间频率和车辆行驶速度相关，空间功率谱密度函数为：

式中　f——车辆行驶过程中轮胎受到的激励频率，f＝u·n，Hz；

u——车速，m／s；将（f1，f2）划分为N 个区间，第i 个区间的中心频率为fmid－i，当N 足够大时，可用fmid－i代替整个小区间上的功率谱密度值，与频率间隔fi 相乘，得到第i 个区间的功率谱密度为：

功率谱与幅值谱间的关系为A2 ＝G，因此可以得到每一段频率对应的粗糙度幅值：

式中　Ai——每一段频率所对应的粗糙度幅值。

将N 个标准差为Ai的余弦波叠加，可得：

式中　Za——垂直于路面的位移，m；将t＝y／u，fi ＝u·ni 代入式（4.5），得：

式中　y——沿着路长方向的位移；

ϕi——［0， 2π］ 上的随机数，满足标准正态分布。

由式（4.6）可知，路面粗糙度的生成与位移相关、与车速无关，车速是参与转换的一个中间变量。 假设沿着路的宽度的方向为x 方向，沿着路的长度的方向为y 方向，路面粗糙度为垂直于x，y 平面的z 方向，沿着路宽和路长方向的粗糙度可用谐和函数来表示。

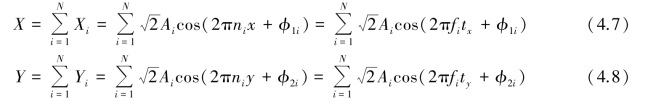
令Z1， Z2，Z3，…，ZN 是N 个独立双变量随机向量，Zi ＝（Xi，Yi），i ＝1，2，3，4，…，N，则向量和为：

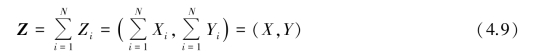
Laning⁃battin 定理中，当N →∞时，Z ＝（X，Y）趋向于正态分布的充分必要条件是：(www.daowen.com)

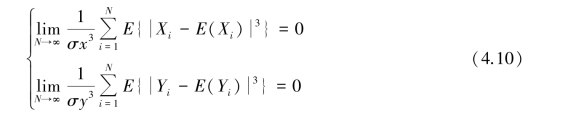
若随机谐和函数Xi 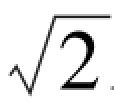＝Aicos（2πfitx ＋ϕi）中，fi，i ＝1，2，3，…，N 相互独立，则其概率密度函数为：

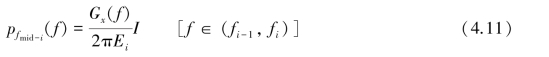
式中　I ［f∈（fi－1，fi）］——示性函数，f∈（fi－1，fi），则I＝1，否则I＝0。

概率具有相容性，因此有：

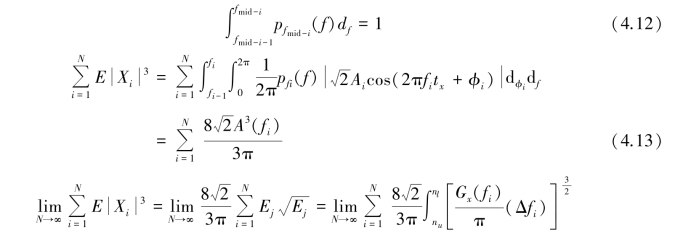
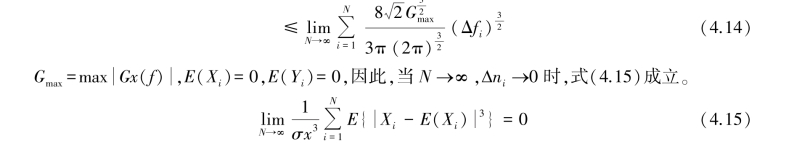
同理可证式（4.10）成立。 根据Laning⁃battin 定理，Z ＝（X，Y）是趋向于正态分布的。 通过Z ＝（X，Y）构造出函数式：

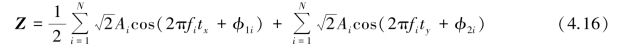
在式（4.6）中已经证明了路面粗糙度与车速无关，只是将时间频率和空间频率相互转化的一个中间参数，将tx ＝x／u，ty ＝y／u，fi ＝u·ni 代入式（4.16），可得：

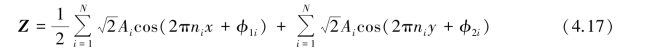
E（X）＝0，E（Y）＝0，X，Y 为独立变量，因此E（Z）＝0。 谐和函数本身具有稳定性，因此当N →∞时，表达的是一个稳定的零均值的趋向于正态分布的过程。

一般路面的空间频率段分布为0.011 ～2.83 m－1，车速范围为10.0 ～40.0 m／s，时间频率范围为0.44～28.3 Hz。 悬挂质量固有频率1～2 Hz 及非悬挂质量固有频率10.0 ～15.0 Hz 包含在此范围内。 将时间频率范围划分为200 份，即N＝200，采样频率为0.01 s，应用式（4.17）通过MATLAB 软件模拟了ISO 规范中C 级路面三维粗糙度，图4.11（a）为随机谐和函数法重构的路的长度和宽度均为40 m 时三维路面粗糙度。 C 级路面粗糙度的变化范围为－0.04～＋0.04 m。 从图4.11（b）中可以看出，在模拟区域内路面粗糙度值呈无规律的随机分布。 图4.11（c）为随机选取的宽度为2.0 m 时的沿着路长度方向的路面粗糙度变化情况，可以看出，路面粗糙度围绕着零值附近波动。 图4.11（d）中将随机谐和函数法生成功率谱密度和标准谱密度相比，模拟的功率谱围绕着标准谱上下波动，其偏离范围不大，拟合情况较好，证明随机谐和函数法生成功率谱密度与标准功率谱有着相近的功率谱密度函数，存在误差主要是因为对路面进行了离散化采样处理，功率谱密度采样点数和随机相位数据有限。 路面粗糙度的变化范围、波动趋势和生成的功率谱密度证明了随机谐和函数法的可行性和正确性，等高线的分布情况证明了其良好的随机性。

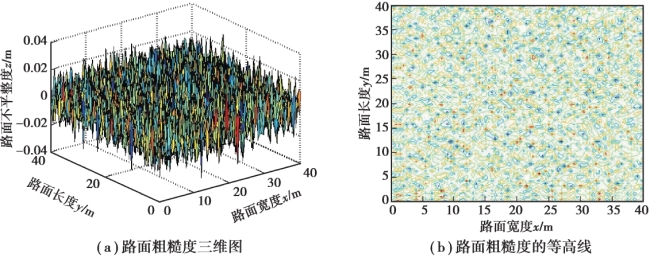
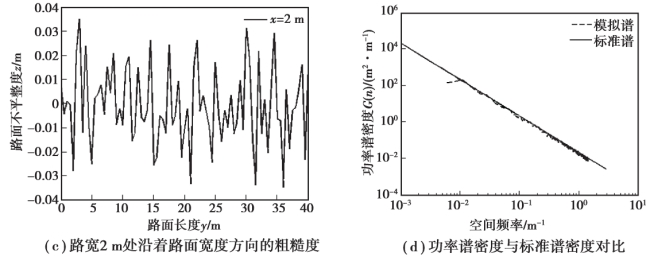
图4.11　随机谐和函数法重构生成C 级路面粗糙度

为了进一步证明提出的随机谐和函数法重构的三维路面粗糙度的正确性和可靠性，用谐波合成法和三角级数法在相同条件下模拟了三维路面粗糙度。 图4.12（a）中可以看出谐波合成法模拟的C 级路面粗糙度变化范围为－0.04 ～＋0.04 m。 比随机谐和函数法生成的路面粗糙度整体略微偏大。 图4.12（b）中路面粗糙度等高线以路面原点处为中心呈圆状向外发散，模拟路面范围内粗糙度值有明显规律。 在以原点为中心、定值为半径的圆上的路面粗糙度值变化接近。 选取宽度为2.0 m 处的路面，路面粗糙度沿着路的长度方向变化，如图4.12（c）所示。 路面粗糙度变化趋势比随机谐和函数法模拟的路面粗糙度变化缓慢，在峰值附近比较明显，而且出现了峰值附近的小范围波动。 谐波合成法生成功率谱密度和标准谱密度相比较的情况，如图4.12（d）所示，模拟的功率谱围绕着标准谱上下波动，其波动范围比随机谐和函数法的功率谱密度要大。 三角级数法生成的C 级路面粗糙度，如图4.13（a）所示，变化范围为－0.04～＋0.04 m。 从其路面粗糙度等高线图4.13（b）中可以看出变化存在明显的规律，在45°斜线方向上的路面粗糙度值基本一致。 图4.13（c）给出了宽度为2.0 m 处的路面，路面粗糙度沿着路的长度方向的变化情况，三角级数法生成的路面粗糙度变化趋势缓慢，沿着路的长度方向逐渐增大和逐渐减小。 因此，三角级数法分析时必须选足够多的采样点才能更好地体现出变化范围。 三角级数法模拟出的功率谱与标准谱如图4.13（d）所示，整体拟合情况较好。

图4.12　谐波合成法生成C 级路面粗糙度

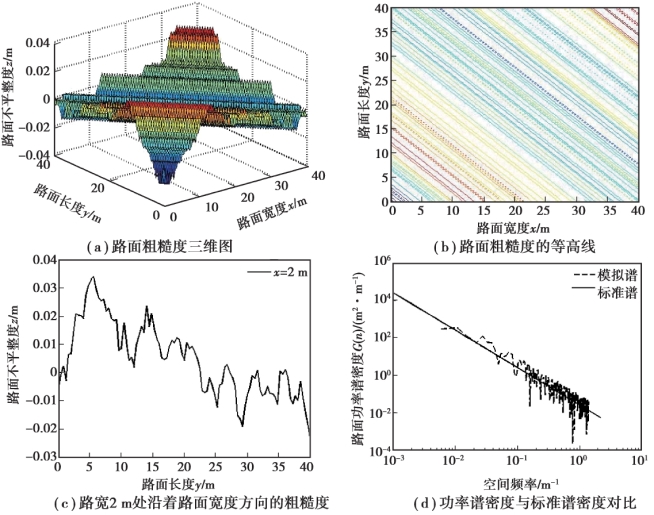
图4.13　三角级数法重构生成C 级路面粗糙度

通过本小节描述可知：

①通过随机谐和函数重构了三维路面粗糙度函数，从理论上证明了该函数为平稳的零均值的趋向于正态分布的函数，与前人研究的假设路面粗糙度为平稳的均值为零的正态分布相符。 用MATLAB 对重构的三维路面粗糙度函数编程，根据模拟结果对生成路面粗糙度的稳定性和零均值性进行验证，把功率谱密度函数与标准谱密度函数相比较，验证了用随机谐和函数法建立的三维路面粗糙度模型的可行性和正确性，同时分析了产生误差的原因。

②在相同条件下应用谐波合成法和三角级数法模拟出了C 级路面粗糙度。 三种方法生成的路面粗糙度变化范围基本一致，但变化速度不同。 三角级数法模拟出的路面粗糙度在沿着路长或者路宽的方向变化最缓慢，随机谐和函数法变化最快速。

③谐波合成法生成的40 m×40 m 路面粗糙度值以原点为中心向外规律圆形发散。 三角级数法生成的路面粗糙度值按45°斜线呈规律性分布。 随机谐和函数法生成的路面粗糙度无规律、随机分布。 三种方法中，随机谐和函数法生成的路面粗糙度随机性相对较好。