图4.1 为节段模型在风洞第二试验段进行的静力三分力试验，图4.2 为通过静力三分力试验测量得到的8.0，10.0，12.0 m／s 风速下静力三分力系数随攻角变化曲线。 在图4.2 中，CH 为阻力系数，CV 为升力系数，CM 为力矩系数，U 为来流风速。

图4.1　静力三分力系数节段模型测力试验

图4.2　不同风速下攻角对三分力系数的影响

由图4.2 可知：

①当风速为8.0，10.0，12.0 m／s 时，每个攻角对应的阻力、升力、力矩系数变化都比较小，3 种风速不同风攻角下，3 条曲线形状十分接近，证明风速变化的情况下雷诺数影响较小，雷诺数效应并不明显。

②风攻角范围在－12°～－8°时，阻力系数随着风攻角的增加而逐渐减小，而在－8°～＋12°范围内随风攻角的增加而变大。

③升力系数在负攻角范围内为负值，先略微下降，最小值位于－8°攻角附近，超过－8°攻角后，其数值随着攻角增加而变大。 0°攻角的升力系数接近于0，但仍为负值。

④力矩系数在负攻角范围内为负值，在正攻角范围内为正值。 力矩系数在正攻角范围内变化的趋势并不明显，超过＋6°攻角后，风速变化对力矩系数基本没有影响。

⑤升力系数曲线和力矩系数曲线的斜率在－8°～＋12°范围内均为正值，证明主梁断面具备气动稳定的必要条件。

为进一步研究攻角变化对宽体式扁平钢箱梁的影响原因和机理，采用Ansys Fluent 模块对10.0 m／s 风速下＋12°，0°，－8°，－12°的4 种攻角进行数值模拟，由于主梁外形沿主跨方向不变，因此处理为二维模型，流动为定常不可压，静力按定常处理，未考虑温度的影响。 对应的数学模型为雷诺时均N⁃S 方程，湍流模型为标准k⁃ε 模型，近壁面以标准壁面函数处理，压力速度耦合选用SIMPLE 算法，离散格式为二阶迎风插值。 数值模拟的缩尺比与节段模型相同，都采用1／60，在前处理软件GAMBIT 中形成计算网格。 为减小边界对断面流场的影响，计算区域设置得足够大：上下边界到断面中心的距离为1.0 m（＞15 倍模型高度），入口距断面中心4.2 m（6 倍模型宽度），出口距断面中心8.4 m（12 倍模型宽度），入口为速度条件，出口为压力出口，主梁及其附属物外壁均为无滑移的wall 壁面。 近壁面第一层网格高度为0.000 5 m，从而壁面Y＋≈30。 为使计算网格更好地适应流场变量的变化情况，在流场变化剧烈的地方划分较密的网格，然后逐渐变稀疏，最大网格尺寸0.02 m，共生成108 416 个网格单元。 应用roughness height 单元模拟桥面粗糙度，近似地将砂纸平均砂粒高度视为桥面粗糙度的厚度。 在划分边界条件时，将模型上表面（包括风嘴）单独设一个壁面wall 边界，求解时，将其roughness height 设为0.97 mm 或1.28 mm 即实现了对B 级（80 目砂纸）和C 级（120 目砂纸）桥面粗糙度的模拟。 在网格划分方面，为了更好地分辨桥面的不平度颗粒，断面上表面划分边界层网格，第一层网格高度为0.05 mm。 图4.3 为计算网格的整体网络划分和局部网络划分图。

图4.3　计算网格划分(www.daowen.com)

为了证明模型的可靠性，应用该模型计算了10.0 m／s 风速时7 种不同风攻角下的静力三分力系数，并将计算结果与风洞试验结果进行对比。 表4.1 为10.0 m／s 风速下数值模拟与试验结果的对比值。

表4.1　10.0 m／s 风速下数值模拟与试验结果的对比值

由表4.1 可知，模拟值与试验值的最大误差为8.921%，最小误差为0.110%，阻力系数平均误差为0.14%，升力系数平均误差为－1.85%，力矩系数平均误差为2.04%，整体平均误差为0.11%。 模拟结果误差较小，因此模型可信度较高，可以用该模型对主梁断面附近流体进行绕流特性分析。 图4.4 至图4.6 中工况（a）～（d）分别对应来流攻角＋12°，0°，－8°，－12°时，主梁断面附近压强、速度和流线分布变化情况，根据其流场的对比可定性分析出静力三分力系数随攻角变化的原因。

图4.4　主梁断面附近压强分布（单位：Pa）

由图4.4（a）可知，主梁上侧处于负压区，下侧基本处于正压区，因此＋12°攻角时，上、下压力差为负，断面竖直方向的受力向上，升力系数为正。 图4.4（b）中主梁上、下侧均处于负压区，而下侧靠近主梁位置形成了几个较小的旋涡，增加了其负压区压强的绝对值，下侧的压强绝对值大于上表面压强，因此上、下压力差为正，主梁断面在竖直方向的受力向下，所以0°攻角时升力系数为负。 图4.4（c）中断面下侧的主旋涡使其处于负压区，其压强绝对值大于0°攻角工况，且上侧为正压，从而上、下压力差为正，且大于0°攻角工况，因此升力系数为负且小于0°攻角工况。 从图4.5（a）～（d）中可知，不同风攻角下主梁附近速度分布与主梁附近流线分布趋势基本保持一致，在风攻角为负时，主梁下侧都出现了高风速带。 图4.5（c）中迎风侧气流的剧烈分离使得斜腹板附近形成了一个高速风带，其风速大于图4.5（d）中的工况，使其迎风侧上部正压区、下部负压区的压强绝对值均大于－12°攻角工况，其上、下压力差大于－12°攻角工况，升力系数更大。

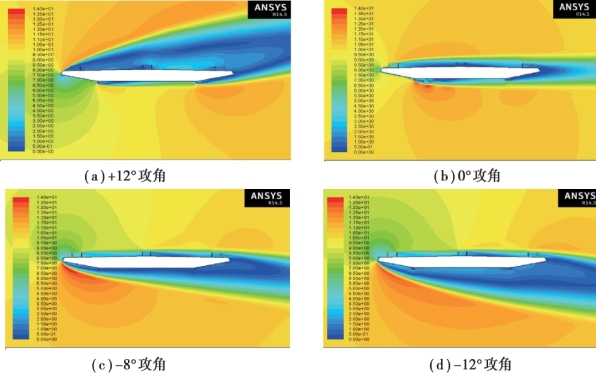
图4.5　主梁附近速度分布（单位：m／s）

扭矩力是由于阻力与升力的合力作用点和断面形心不一致而形成的。 图4.4（a）中＋12°攻角工况的断面迎风侧下方为正压，断面上方、下游为负压，因此，力矩为顺时针方向，力矩系数为正；图4.4（b）中0°攻角工况时，竖直方向的升力接近于0，合力作用点与形心接近，力矩系数接近于0；图4.4（c）和图4.4（d）中风攻角为负数时迎风侧上方为正压，迎风侧下方及下游均为负压，因此，力矩为逆时针方向，力矩系数为负。 综上所述，力矩系数在负攻角范围内为负值，在正攻角范围内为正值。

从图4.6（a）中可看到气流在风嘴处迅速发生分离，断面上表面形成大范围的主旋涡，并延伸至背风侧下游的尾迹区，上表面及背风侧均为负压。 因此，上、下压力差，迎、背风侧压力差均为正值，即升力系数、阻力系数均为正。 图4.6（b）中，气流由风嘴处开始分离，风嘴的导流作用使得分离过程较平缓，从而迎风侧端部的正压区较＋12°攻角工况小，迎、背风侧压力差及阻力系数均减小；图4.6（c）、图4.4（d）中，迎风侧斜腹板处形成的旋涡使其处于负压区，迎、背风侧压力差及阻力系数都比0°攻角工况小。 图4.6（d）中，迎风侧斜腹板处的旋涡与断面下方分离区旋涡汇合成一个大的主旋涡，且一直延伸至下游，使其背风侧负压区的范围与压强绝对值均大于－8°攻角工况，因此其迎、背风侧压力差更大，阻力系数更大。图4.6（c）中，在迎、背风侧斜腹板处分别形成了单独的旋涡，使得断面下方出现两个负压区。从图4.5（c）中可看出，迎风侧旋涡风速更大，负压区压强绝对值更大，因此，迎、背风侧压力差为负值，阻力系数为负。

图4.6　主梁附近流线轮廓