运用ANSYS 软件在风攻角取0°的情况下，对该悬索桥进行完全瞬态动力分析。 10 m处的设计基本风速为28.1 m／s，按照实测风剖面幂指数函数计算得到桥梁结构各高度处的来流平均风速，采用一致质量矩阵计算；结构的阻尼使用瑞利阻尼，阻尼比为0.005，时间步长为0.125 s，计算时间为600 s。 升力、阻力、扭转气动导纳系数和气动导纳系数导数取值均为1。

对主梁上60 个节点的位移时程结果进行均方根计算，得到主梁上的位移响应RMS 值。图3.12 中给出了主梁横桥向、竖桥向及扭转抖振位移RMS 值。 图3.13 中给出了主梁跨中节点横桥向、竖桥向及顺桥向扭转位移时程曲线。

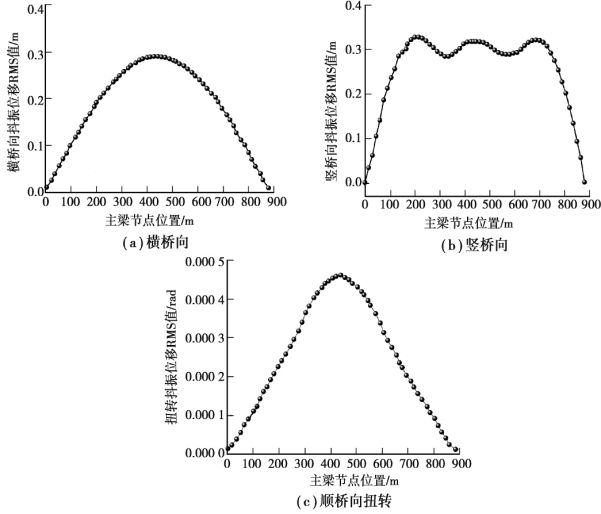
图3.12　主梁抖振位移RMS 值

由图3.12 可知，主梁抖振位移RMS 值均以跨中节点为中心，基本呈对称状态。 横桥向的RMS 值由主跨跨中向两侧递减，在梁塔交接处最小，出现这一现象的原因是主梁与主塔之间设置了抗风支座，限制了主梁的横桥向位移。 横桥向、竖桥向及扭转抖振位移的最大RMS 值分别为0.290 m，0.327 m 和0.000 46 rad。 由图3.13 可知，在计算时间600 s 内，主梁跨中横桥向和竖桥向抖振位移峰值分别为1.432 m，1.145 m，其扭转抖振位移峰值为0.001 4 rad。

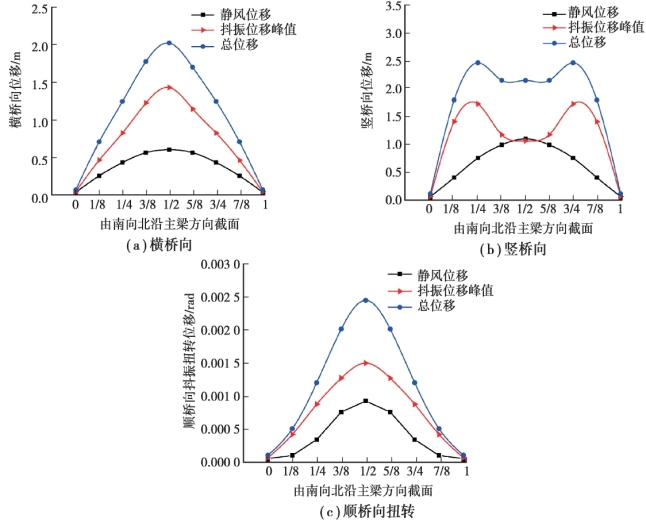
为研究脉动风荷载对桥梁的抖振位移和内力的影响，分别计算了仅有静风荷载作用在桥上、脉动风荷载同时作用在桥梁上两种工况下的桥梁典型截面位移值及内力值。 图3.14为两种工况下桥梁典型截面的位移值对比情况。

表3.6 和表3.7 中分别给出了有无脉动风作用下桥梁典型截面抖振力和抖振弯矩的对比值，结合图3.12 和图3.14 可以看出：

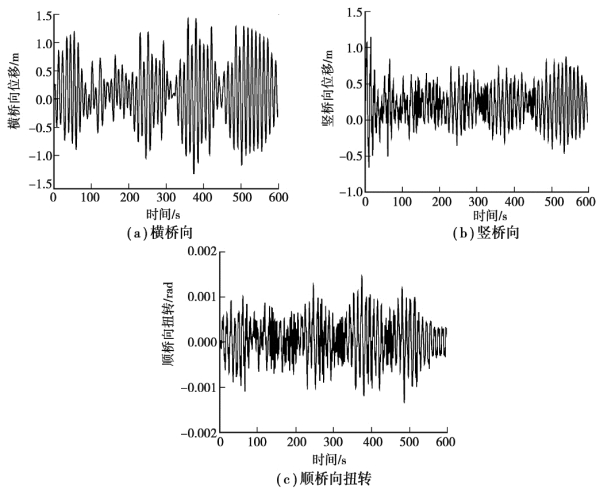
图3.13　主梁跨中节点位移时程曲线

(www.daowen.com)

图3.14　抖振位移峰值和静风位移值对比

表3.6　桥梁典型截面抖振力和静风力值对比

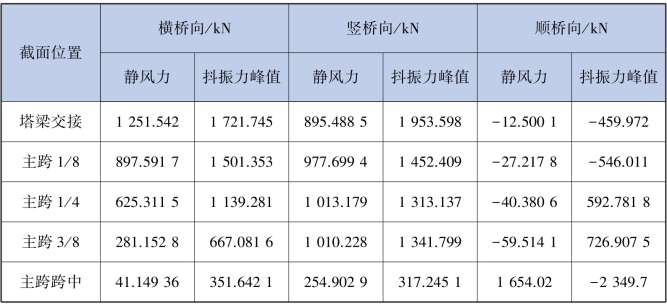
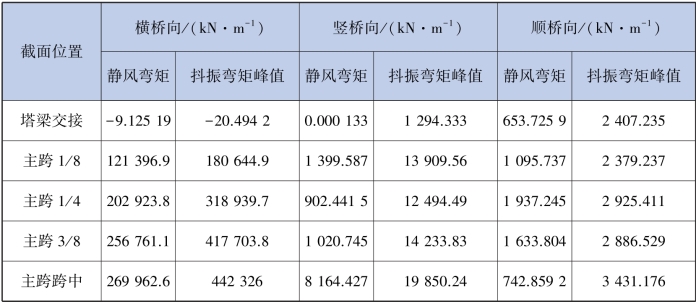
表3.7　桥梁典型截面抖振弯矩和静风弯矩值对比

①主梁竖向抖振位移的最大处不是在主梁的跨中，而是在主梁的1／4 处附近。

②主梁横向抖振位移响应和扭转响应最大值均出现在跨中的位置。 这是因为对于抖振竖向位移响应，前几阶自振模态贡献较大，而前几阶自振模态中，反对称振型占的比重较大，叠加后的结果就是主梁的1／4 处位移较大。 而对于抖振横向位移响应和扭转响应，主要是第一阶振形起主导作用，而第一阶振型又为对称振形，故跨中处位移最大。

③平均风荷载引起桥梁的位移和内力响应比较小，脉动风荷载引起的桥梁的位移、内力值为平均风荷载的几倍，脉动风引起抖振响应对该桥影响显著，在设计和运营中应特别注意考虑抖振力引起的疲劳破坏，在风⁃汽车⁃桥梁系统振动的计算中必须要考虑抖振响应。