由于主塔截面为变截面，故采用beam44 单元（空间变截面梁单元）模拟，主梁采用传统的单梁形式，主梁截面基本可看成沿桥走向不变化，采用beam4 空间梁单元，本书建模时吊杆与主梁之间的连接采用刚臂连接法。 吊杆和主缆属于二力构件，在ANSYS 中采用杆单元link10 来模拟，该单元每个节点有3 个自由度。 二次铺装质量及灯塔栏杆等质量及质量惯性矩通过质量单元mass21 单元施加。 主缆的垂度用Earnst 式来考虑，主梁与塔上横梁之间的约束采用耦合自由度考虑，考虑了3 个方向自由度的耦合，即竖向Uy、侧向Uz 和绕桥轴向的扭转rotx。 表3.2 给出了建模时选用的单元类型，表3.3 给出了对应的材料类型。

表3.2　单元类型

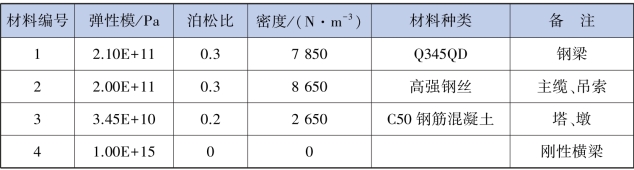
表3.3　材料类型

主缆及吊索的初应变采用成桥状态分析结果，结构的质量为成桥状态的质量，边界条件为：

①主缆的锚固处为固定约束，塔柱在承台顶面处嵌固。

②塔和梁的交接处，梁的竖向、横向及绕顺桥向的扭转位移有塔梁约束，其他自由度均为释放。

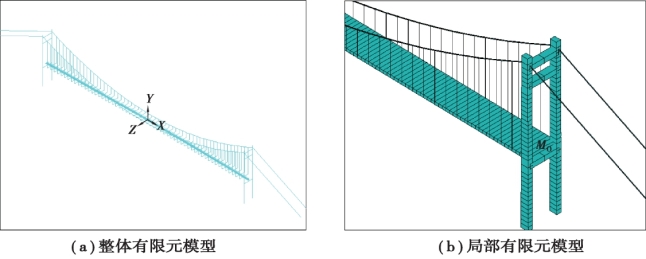
③塔梁交界处的阻尼器支座用弹簧阻尼单元模拟。 按上述边界条件基于ANSYS 平台建立了寸滩长江大桥三维空间有限元计算模型，其模型如图3.7 所示。 通过该模型计算出有限元的动力特性，得到了模型的固有频率和振型特点。

(www.daowen.com)

图3.7　寸滩长江大桥有限元模型

表3.4 中给出了通过软件计算出的桥梁有限元模型的前20 阶模态频率。

表3.4　寸滩长江大桥动力特性

由表3.4 中可知，该桥的前20 阶模态频率分布区间为0.112 2 ～0.470 2 Hz，同为悬索桥的江阴大桥前20 阶模态频率分布区间为0.051 6～0.342 8 Hz，西堠门大桥前20 阶模态频率分布区间为0.048 3 ～0.259 3 Hz，润扬悬索桥前20 阶模态频率分布区间为0.049 4～0.274 1 Hz，南京长江第四大桥前20 阶模态频率分布区间为0.064 99～0.299 07 Hz。 通过比较发现，寸滩长江大桥基频较高，基本周期相对较短，桥梁整体频率分布区间较广。 如果相同车流对桥梁进行周期性的激励，车辆和桥梁之间有可能发生共振现象。 而悬索桥本身特点为柔性相对较大、刚度较小，因此，桥梁抗风性能为其设计、施工及运营阶段的主要控制因素。 图3.8为该桥前10 阶振型图。

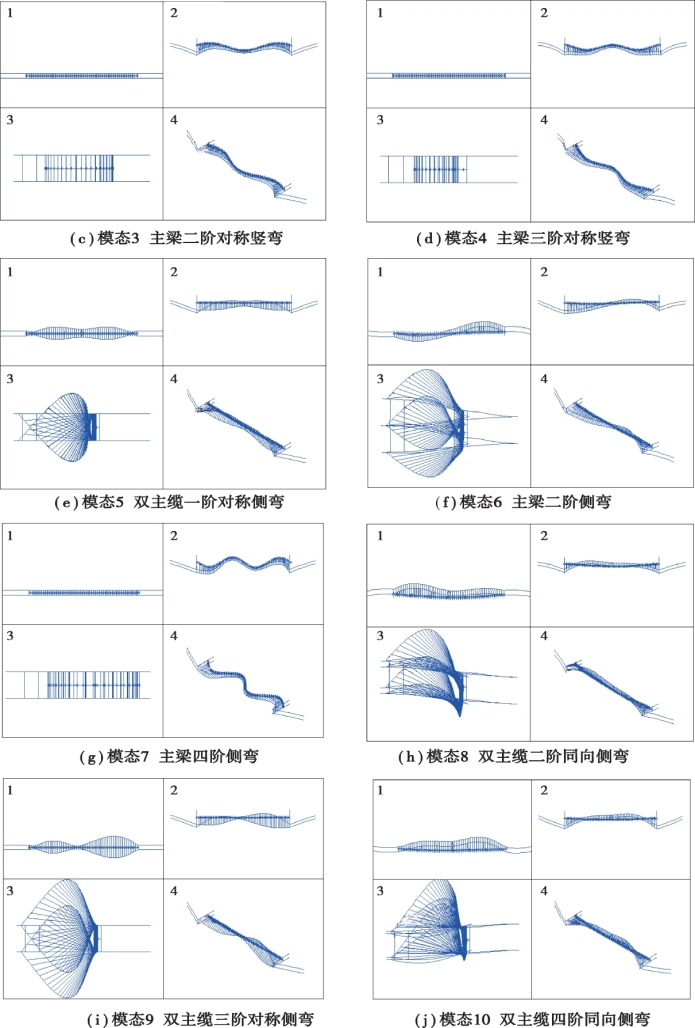
图3.8　寸滩长江大桥前十阶振型模态

由图3.8 可知，寸滩长江大桥基频为0.112 2 Hz，基本周期较短，其对应振型为主梁一阶对称侧弯振型；第二阶振动频率为0.116 2，其对应振型为主梁一阶反对称竖弯振型，符合大跨度悬索桥这一柔性结构的动力特性的基本规律。 在前20 阶振型中，未出现以主塔振动为主的振型，出现的都是以主缆和主梁的振动为主的振型，推测其原因为悬索桥的主塔结构的刚度要远大于主缆和主梁的刚度。 主梁的第一阶振型为横向侧弯振型，这表明此宽体式扁平钢箱梁的横向振动问题将会比较突出，进行抖振分析时，应特别注意主梁的侧向位移。 但进行车辆⁃桥梁系统振动分析时，横向激励通常被忽略，因此后续车辆⁃桥梁振动系统中未分析桥梁的横向响应。