1）湍流度

在2014 年8 月26 日2：25—2：35 时段内，根据10 m 高度处10 min 的顺风向、横风向和竖风向脉动风速数据记录结果，得到顺风向、竖风向和横风向3 个方向的脉动风速，如图2.14所示。 在2014 年8 月26 日，10 m 高度处10 min 的顺风向、横风向和竖风向脉动风速24 h记录数据，如图2.15 所示。

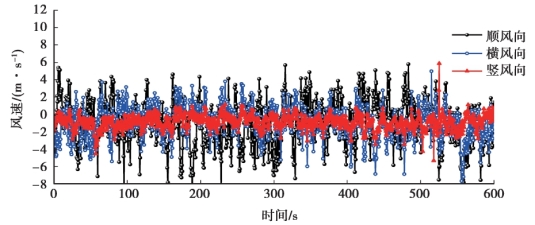
图2.14　10 min 3 个方向脉动风速记录

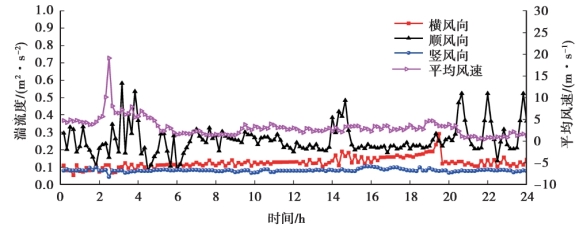
图2.15　10 m 高度处湍流强度变化曲线

根据图2.14 中可计算出3 个方向的脉动风速均方差分别为2.934，2.054，0.883；3 个方向的湍流度为0.154，0.107，0.046，其比值为1 ∶0.73 ∶0.26。 根据图2.15 可计算出3 个方向的脉动风速均方差分别为0.781，0.381，0.243。 2014 年8 月26 日，10 m 高度处24 h平均风速为3.1 m／s，3 个方向的湍流度为0.253，0.123，0.078，其比值为1 ∶0.48 ∶0.31。

本次观测中记录到的风速样本较多，为了便于分析，在数据处理中，先根据原始数据计算不同高度观测设备在10 min 时距内顺风向脉动风速、横风向脉动风速和竖风向脉动风速的均方根与水平平均风速的比值，分别得到这三个方向的湍流强度，然后再通过加权平均得到每一天的湍流强度值，最后得到10 m 高度处湍流强度随时间的变化规律。 图2.16 为2014 年7 月3 日和2014 年9 月18 日两次测到的3 个方向湍流度及平均风速图。

由图2.16（a）可知，2014 年7 月3 日最大风速11.2 m／s 发在18：10—18：20，平均风速为3.4 m／s，顺风向湍流度平均值为0.304，最大值为0.399，横风向湍流度平均值为0.204，最大值为0.291，竖风向湍流度平均值为0.108，最大值为0.132，其比值为1 ∶0.67 ∶0.35。由图2.16（b）可知，2014 年9 月18 日最大风速10.3 m／s 发在17：20—17：30，平均风速为4.9 m／s，顺风向湍流度平均值为0.178，最大值为0.660，横风向湍流度平均值为0.114，最大值为0.309，竖风向湍流度平均值为0.034，最大值为0.062，其比值为1 ∶0.64 ∶0.19。 本书给出了观测期间16 次大风的湍流度及当日平均风速（表2.9），从表中可看出湍流度比值与《规范》所给偏差较大，10 m 高度处16 次大风的顺风向湍流度平均值为0.251，横风向湍流度平均值为0.161，竖风向湍流度平均值为0.111，其顺风向湍流强度较大，容易引起抖振响应。 由图2.16 可看出平均风速增加时湍流度呈减小的趋势，推测其原因为平均风速较大时，气流稳定性较好，因此湍流度小；当平均风速较小时，气流稳定性差，因此湍流度大。

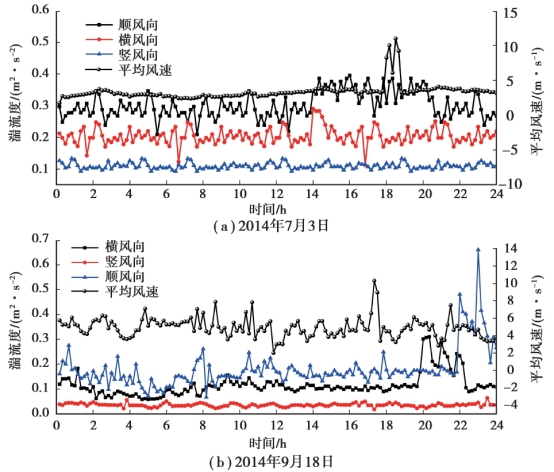
图2.16　湍流度及平均风速图

表2.9　观测期间16 次大风的湍流度及当日平均风速

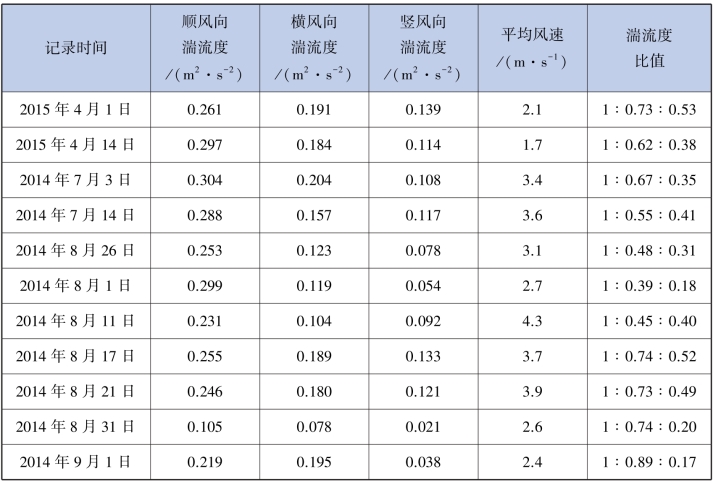
续表

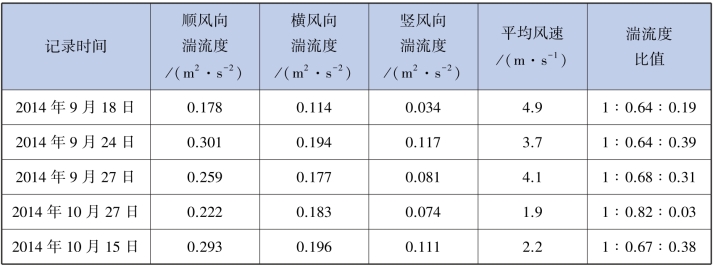
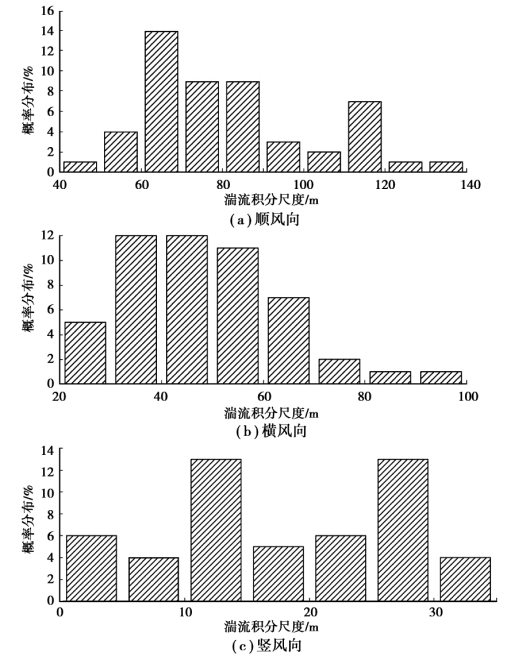
图2.17　湍流度分布直方图

2）湍流积分尺度

湍流积分尺度在较大范围内会发生波动。 对观测期记录到的51 次强风10 min 数据样本进行分析统计。 图2.17 中给出了51 次强风的三个方向的湍流度概率分布情况，其中横坐标表示湍流积分尺度，顺风向和横风向以10 m 间隔作为一个计算区域，竖风向以5 m 间隔作为一个计算区域，纵坐标为对应的概率分布。

由图2.17 可计算出顺风向湍流积分尺度最大值为136.0 m，最小值为49.1 m，平均值为81.8 m，大部分集中在60 ～90 m。 横风向湍流积分尺度最大值为93.5 m，最小值为21.6 m，平均值为49.1 m，大部分集中在30 ～70 m。 竖风向湍流积分尺度最大值为32.2 m，最小值为1.4 m，平均值为17.6 m，大部分集中在10 ～30 m。

图2.18 为记录到的强风数据的最大风速和三个方向湍流度的关系。

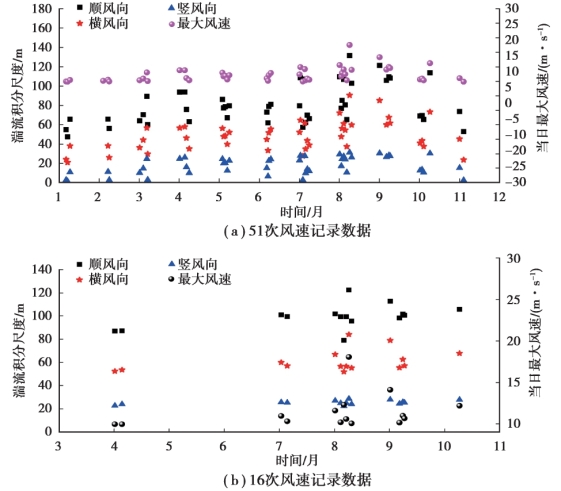
图2.18　平均风速与湍流度之间的关系(www.daowen.com)

由图2.18 可知，在51 次6.0 m／s 以上风速记录数据中，8 月26 日风速为25.2 m／s 时湍流积分尺度最大，顺风向、横风向和竖风向分别为136.0，95.4 和32.3 m。 1 月21 日风速为6.0 m／s时湍流积分尺度最小，顺风向、横风向和竖风向分别为49.0，21.6 和1.4 m。 整体上湍流积分尺度随平均风速的增大有增大的趋势，因为风速高时，气流稳定性好；风速较低时，气流稳定性差，很容易被耗散掉。

3）脉动风功率谱

脉动风中高低频率对结构的影响能够通过脉动风功率谱函数体现。 获取一个地区准确的脉动风速功率谱函数的方法是：在实测风速数据的基础上进行函数拟合。 在处理脉动风谱实测数据时，为了减少谱值产生的随机误差，使用了分段平滑技术。 如果信号在时域中被截断，在频域中会发生泄漏，为了减少这一现象，使用了Hamming 窗技术。 在进行脉动风速功率谱拟合时，用到的数据为16 次10.0 m／s 以上的大风记录数据。 以每个样本出现月最大风速值的点为中心，向前后各延长5 min 得到10 min 共计1 200 个点的数据，将其分成8 段，每段包含150 个数据。 为了得到更稳定的功率谱值，数据段之间采用了20%的重叠进行过渡。 应用快速傅里叶变换（FFT）实现功率谱从时域到频域的转换。 《规范》中，顺风向脉动风功率谱为Simiu 谱，横风向脉动风功率谱为Panofsky 谱，以此为基础，顺风向和竖风向脉动风功率谱的拟合式分别为式（2.30）和式（2.31），需要拟合参数为Au，Aw，Bu，Bw。

风速过低时不能引起风致振动，通常研究的结构抗风范围都为强风，只有强风才能引起较大的振动，影响桥梁结构的安全，因此在研究脉动风功率谱时，选择的风速样本为观测系统中记录到的16 次强风。 图2.19 为2015 年4 月14 日、2014 年8 月26 日、2014 年9 月18日和2014 年10 月15 日4 次顺风向脉动风速谱的实测功率谱、拟合功率谱和标准功率谱的对比情况。

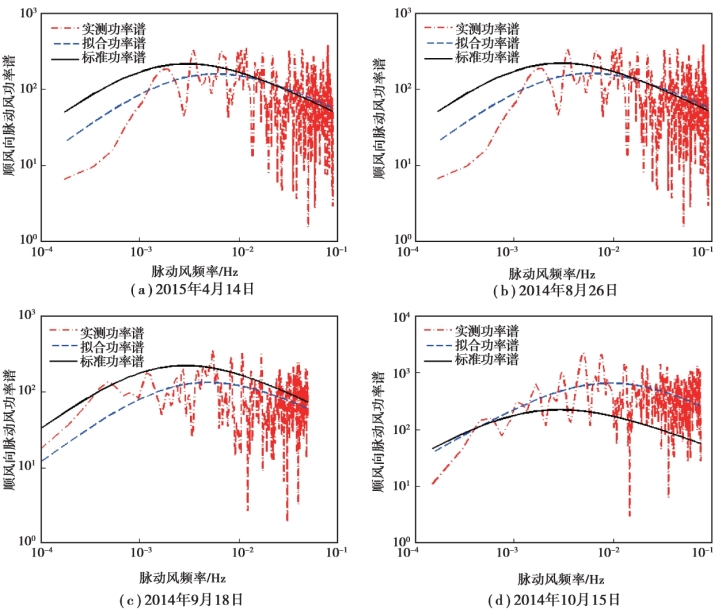
图2.19　顺风向脉动风速谱

图2.20 为2015 年4 月14 日、2014 年8 月26 日、2014 年9 月18 日和2014 年10 月15日4 次竖风向脉动风速谱的实测功率谱、拟合功率谱和标准功率谱的对比情况。

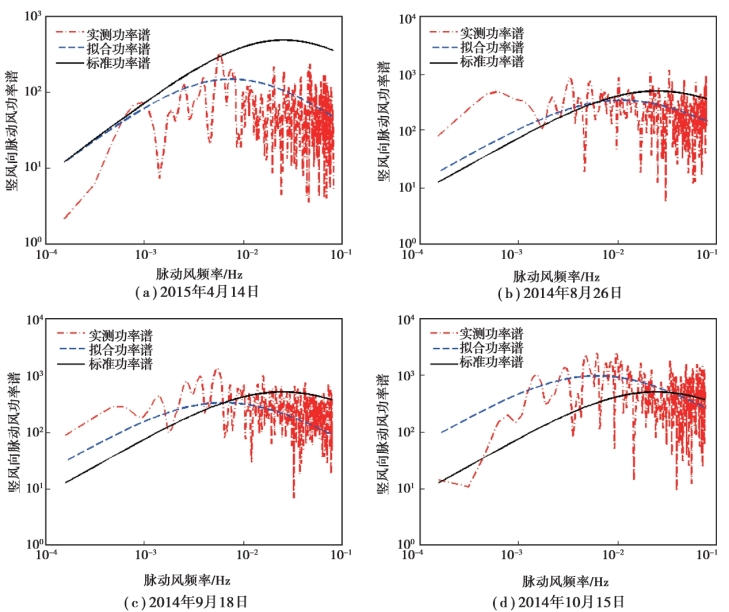
图2.20　竖风向脉动风速谱

由图2.19 和图2.20 可看出：

①实测顺风向和竖风向湍流功率谱函数与规范谱都不一致。 证明桥址处的风场特性与《规范》中的风场特性不同，《规范》所给定的功率谱参数适用于比较平坦的地区，而对于西部山区，实测谱与规范谱存在着较大偏差。

②顺风向多数实测谱在高频率段比规范谱大，低频率段比规范谱小，表明实测脉动风在水平向上的湍流动能分布向高频率段发生了偏移。

③竖风向刚好相反，多数实测谱在低频率段偏小，而在高频率段偏大，表明实测脉动风在垂直方向上的湍流动能分布向低频率段发生了偏移。

④脉动风功率谱值随风速的增加有增大的趋势。

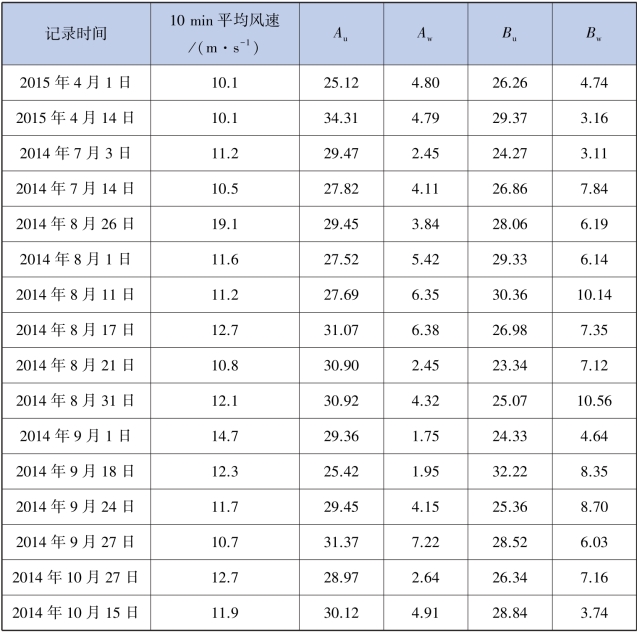
⑤对16 次脉动风速记录进行拟合，得到其变量Au，Aw，Bu，Bw的值，见表2.10。

由表2.10 可计算出Au，Aw，Bu，Bw 的平均值分别为29.31，4.22，27.22，6.56。 因此，桥址处的顺风向（横桥向）和竖风向（竖桥向）脉动功率谱式为：

表2.10　变量拟合值