1）湍流强度

通过3 个正交方向（顺风向、横风向和竖风向），根据瞬时风速分量计算，通常情况下，顺风向的湍流强度值要比其他两个方向的湍流强度值大。

风速沿纵桥向、横桥向、竖桥向3 个分量分别为Vx，Vy 和Vz。

湍流强度Iu，Iv 和Iw：

式中　σu，σv，σw——u（t），v（t）和w（t）的均方根。

依据式（2.7）和式（2.8），可以通过实测的风速值计算出湍流强度。

表2.4　顺风向湍流强度Iu

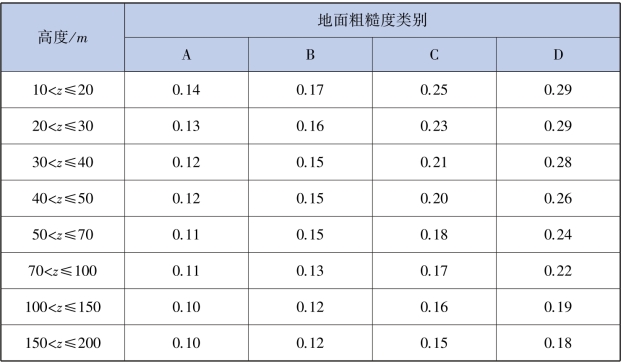
从表2.4 中可知，湍流强度与高度和地表类型有关。 当顺风向的湍流强度Iu按表2.4 选取时，横风向的湍流强度Iv ＝0.88Iu，竖风向的湍流强度Iw ＝0.50Iu。

2）湍流积分尺度

湍流积分尺度为：

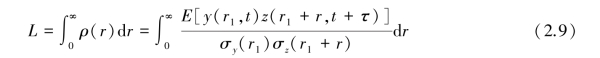
式中　ρ（r）——互相关系数；

r——两点间距。

3 个方向的湍流积分尺度为：

水平纵向：

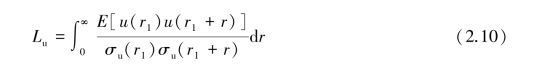
水平横向：

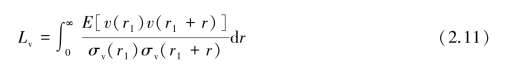
竖向方向：

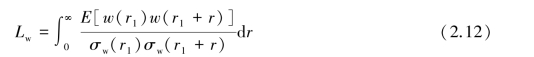
式中　u，v，w——顺风向、横风向和竖风向的脉动风速。

3）脉动风功率谱

脉动风功率谱表示湍流中不同尺度的旋涡对湍流动能的贡献大小，可以由建立在一定假设基础上的理论推导得到，也可以由气象站实测风速记录的相关函数经过快速傅里叶变换而得到。 假定Si（i＝u，v，w）为脉动风功率谱，为对应的脉动动能，则有：

式中　i＝u，v，w——水平、横向和竖向；

n——频率。

根据Kolmogorov 相似原理，大气边界层近地区域内无量纲脉动风速功率谱密度函数的一般形式为：

式中　Si（i＝u，v，w）——湍流功率谱密度函数；

u∗——摩擦速度；(www.daowen.com)

Ai（i＝u，v，w）——近似为0.27，0.36，0.36。

脉动风功率谱的归一化功率谱一般形式可表示为：

式中　Ai，Bi，γi，δi——需要拟合的无量纲系数。

根据是否考虑湍流积分尺度随高度的变化，将脉动风功率谱分两类，其表达式如图2.2所示。

1962 年，Davenport 提出了著名的Davenport 谱：

式中　Su（n）——水平顺风向脉动风功率谱；

U10——平均风速；

n——脉动风频率，Hz；

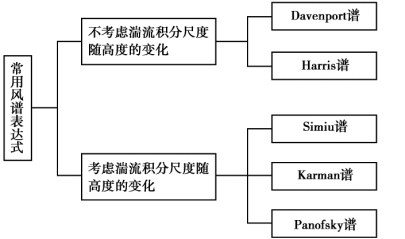
图2.2　常用风谱表达式

k——地面粗糙度系数；

1 200——湍流积分尺度L ＝1 200 m。1970 年，Harris 等给出了修正脉动风功率谱，Harris 风速谱表达式为：

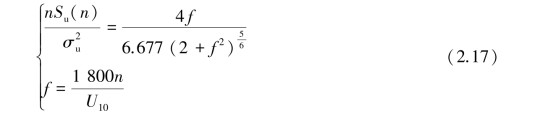
1972 年，Karman 等提出了随离地高度变化的纵向脉动风功率谱，即Karman 谱：

式中　Su（n）——水平向脉动风功率谱；

n——脉动风频率，Hz；

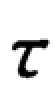0——剪切力；

ρ——空气密度；

f——折算频率，f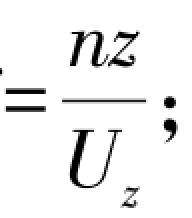

Uz——基本风速。

1974 年，Emil Simiu 等提出了能考虑随高度变化的顺风向脉动风速湍流功率谱，即Simiu 谱，采用分段函数表示为：

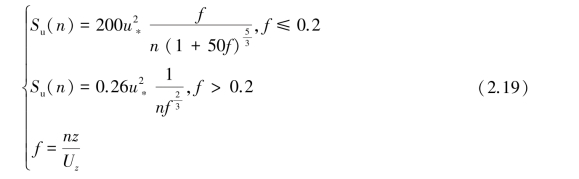
《规范》中水平方向采用了Simiu 脉动风速谱：

垂直方向脉动风功率谱常采用Panofsky 谱：

式中　z——高度；

u∗——摩阻速度。