地震方法的基础是地震波在岩石中的传播规律,而岩石的弹性性质决定了地震波的传播规律。讨论地震波的传播问题时,须应用弹性力学的原理,并假设地球介质是均匀的、连续的、各向同性的和完全弹性的。
讨论地震波传播时,把地球介质作为理想的弹性介质,在震源(外力)作用下,周围介质会发生形变。应力和应变是描述外力和形变之间关系的两个最基本的概念。
作用在物体上的力分为体力和面力。作用在物体表面的力称为面力。应力是面力,它与作用点的位置和面的方向有关。应变则是应力所引起物体形变的一种量度,它们是由邻近质点的相互作用而产生的。应变分为线应变、切应变和体应变。在弹性限度内,应力与应变遵从胡克定律,即应力与应变成正比。
2.3.2.1 弹性常量
在描述介质弹性性质时常使用以下弹性模量。弹性模量也叫弹性参数或弹性系数,它表示了弹性体应力与应变之间的关系,反映了弹性体的弹性性质。
(1)杨氏模量E:在纯伸长或压缩情况下,E为纵向应力F/S和纵向应变ΔL/L的比值(图2.3-3)。

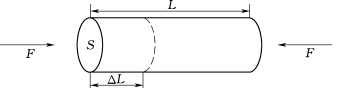
图2.3-3 纵向应力与纵向应变关系图
(2)体积模量K:纯流体在均匀静压力P下引起的体积应变为ΔV/V,则体积模量

它的倒数![]() 为压缩系数。
为压缩系数。
(3)切变模量μ(又称刚性系数):单纯发生切应力(剪应力)时,切应力F/S和切应变ψ(形变角)的比。
![]()
(4)泊松比σ:如对物体施以张力,不仅沿力的方向上物体伸长ΔL,同时在与力相垂直的方向上缩短Δd,我们称与力相垂直的方向上所产生的形变与沿力方向上所产生的形变的比值为泊松比σ。
![]()
上述的E、K、μ、σ四个弹性常量都是由物体本身的性质所决定的。这四个弹性常量中只有两个量是独立的,知道其中任意两个,另两个可根据下面公式求出。
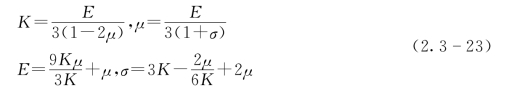
(5)拉梅常量λ:定义为
![]() (www.daowen.com)
(www.daowen.com)
与上述四个弹性常量的关系为
![]()
很多固体,特别是地表附近的岩石,其泊松比σ接近于1/4,拉梅常量λ=μ。
(6)地震波速度。
纵波速度

横波速度

(7)波速与弹性常量关系:
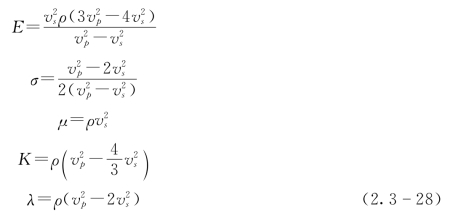
2.3.2.2 波动方程与地震体波
波动方程是为研究介质中质点位移随时间和空间的变化规律,根据牛顿第二定律F=ma,建立起来的质点位移所满足的方程。
以下对连续介质内部一个质元,即图2.3-4中通过P点的小平行六面体作微小扰动时应用牛顿第二定律。对于各向同性的弹性介质,在略去外力的情况下,可得到该质点用位移表示的运动方程式:
![]()
式中 ui为x方向上的位移;λ和μ为拉梅常量和切变模量;∇2为拉普拉斯算子;θ=∇·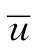 为体积应变;ρ为介质密度。
为体积应变;ρ为介质密度。
同理,得出均匀、各向同性、理想弹性介质中的三维波动方程式为
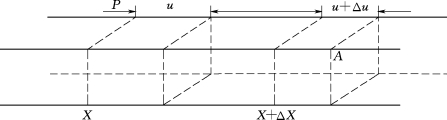
图2.3-4 作用于体积元上的应力
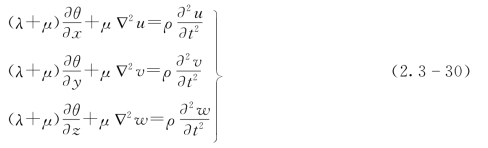
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






