2.3.1.1　麦克斯韦方程

所有的电磁现象都可以用经验的麦克斯韦方程来描述。麦克斯韦方程是一组互相独立的线性微分方程。在时间域中，麦克斯韦方程有如下形式：

式中　e为电场强度，V/m；b为磁感应强度，Wb/m2；d为电位移，C/m2；h为磁场强度，A/m；j为电流密度，A/m2；ρ为电流密度，C/m3。

利用矢量场函数解边值问题常常是很困难的，一般利用矢量势和（或）标量势来求解。从势函数可以推出矢量场函数。我们采用的是谢昆诺夫势，因为它具有对称性，并易于同TE和TM激发模式建立关系。均匀无源区域的电磁场总是可以分解成两部分：一部分的电场分量垂直于某一轴线（TE模式）；而另一部分的磁场分量垂直于这同一个轴线（TM模式）。模式分解简化了边界值问题的解。

对于由多个均匀各向同性的线性区域拼接起来的大地模型来说，每一个区域都需要有一个波动方程的解。根据预先设定的关于两个矢量场函数或势函数的边界条件，在每个区域的边界上这些解必须相互一致。每一个区域的波动方程都是从麦克斯韦方程组直接推导出来的，是麦克斯韦方程组的简洁表达形式。无源的区域用齐次波动方程描述，有源的区域用非齐次波动方程描述。

时间域中电场和磁场的波动方程为：

将式（2.3-5）和式（2.3-6）相对时间做傅氏变换，得到

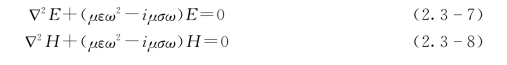
或者

式中

式（2.3-7）～式（2.3-11）就是频率域中的波动方程，当频率小于105Hz时，对大地介质有μεω2≪μσω，即位移电流远小于传导电流。

2.3.1.2　点电流源的地中电场

（1）点电流源在地面。设地面为无限大平面，地下充满均匀、各向同性的导电介质，当点电流源A在地表向地下供入电流I时，地中电流线的分布便以A为中心向周围呈辐射状，如图2.3-1所示。

(www.daowen.com)

图2.3-1　地面上一个点电源的电场

为了求距A为R的M点之电位，可用均匀无限介质中点源电场的拉普拉斯方程解。另外，注意到半无限介质中，电流密度应较无限介质中大一倍，则有

从而可得：

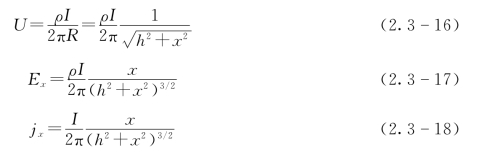
因此M点电位及电场强度分别为：

可见，地中点源电流场的电位、电流密度和电场强度均与供电电流I成正比，而U与R成反比，E及j与R的平方成反比。

（2）点电流源在地下。如图2.3-2所示，当点电流源A位于地下h深度时，地中电流分布不再呈辐射状。由于在地表电流密度的法向分量应等于零，为满足此边界条件，可用镜像法求解，即假设在地面以上也充满电阻率为ρ的介质，而在电源A与地面对称位置上设一虚电流源A′，且使二者电流相等。地中任一点的电位便为

式中　R′为M点与虚电源A′间的距离。

图2.3-2　地下点电流源的电场分布示意图

当观测点M是位于地面时，R=R′，此时

电位分布曲线如图2.3-2上图所示，在A的正上方电位具有极大值，向两边逐渐减小，在x=的两点上，电位等于极大值的一半，x=的两点为电位曲线的拐点位置。不难想象，在地面上等位线是以0点为圆心的同心圆簇。如果相邻等位线间的电位差相等，则等位线在拐点附近密集而在0点附近和远处渐稀。在x=0处，电场强度等于零。两侧的电场强度E曲线以0点反对称，这是电流自0点向两侧流出造成的。在电位曲线的拐点处，电场强度出现极值。在x=0和x=的地方，E有三个拐点。电流密度的分布规律与电场强度完全相同，两者只在量值上差一个系数ρ。