1. 概述

由于建立的内陆型集装箱中心站开行方案模型是非线性的，求解该类模型，大多依赖启发式算法，包括遗传算法（Genetic Algorithm）、粒子群算法（Particle Swarm Optimization，PSO）、模拟退火算法（Stimulated Annealing，SA）与蚁群算法（Ant Colony Optimization，ACO），不同算法特点比较分析如表6-1所示。

表6-1　不同算法比较分析

由于在中欧班列开行方案设计中涉及的路径节点比较多，单个节点与其他节点存在较多联系，路网比较复杂，节点数量增多时，求解工作量比较大，相应的求解难度较大，所以，本书选用遗传算法来求解路径优化问题。

2. 遗传算法

1）遗传算法概述

遗传算法（GA）是由约翰·霍兰（John Holland）等人于1975年首次提出。作为一种全局性优化方法，遗传算法在物流与供应链管理领域处理了大量的优化问题。基本思想是用生物中的染色体来求解问题，把这些染色体置于问题求解的环境中，根据优胜劣汰的原则，选择适应环境的优良个体进行复制、交叉、变异，产生更适应环境的新一代染色体群。在实际应用中，遗传算法能够不依靠问题本身迅速搜寻未知空间以便找到高适应值点。

2）遗传算法的特点

遗传算法的优越性主要体现在：一是在搜索过程不会轻易陷入局部最优困境，尽管所定义的适应函数处于不连续、非规则的情况，仍然会有较大的概率找到整体最优解；二是由于本身固有的并行性，对于大规模的计算，遗传算法都可以解决。为了避免陷入局部最优，在遗传算法中引入了变异。一方面可以在附近找到更好的解，另一方面能够保持群体的多样性，保证群体能够继续进化。遗传算法在很多领域应用广泛，比如在函数优化、组合优化、生产调度、图像处理等领域。

3）遗传算法基本流程

遗传算法的遗传操作具有随机性，可以有效通过历史信息来推测下一代性能，可以提高寻优点集。通过群体一代一代不断进化，最终收敛到适应环境的优良新个体上，得到问题的最优解。遗传算法的运行过程是一个典型的迭代过程，其基本算法流程如下所示。

（1）编码策略。二进制编码方式是比较常见的策略，染色体为n位的二进制串，第i个基因位为0，表示第i列未被选中，否则表示第i列包含在解中。通过交叉、变异后，需要检验新解是否可行，消除冗余列；并需设计启发式算法将非可行解转化成可行解或在非可行解的目标函数值上加罚函数值。(www.daowen.com)

（2）计算适应度函数。用适应值来衡量个体优劣，表明个体对环境的适应能力。遗传算法在搜索时的依据是适应度函数，即遗传算法的收敛速度、能否找到最优解等取决于所选择的适应度函数。对于函数优化问题，一般取目标函数作为适应度函数。

（3）选择。在生物进化过程中常常伴随着一定的随机性，其中适应环境能力比较强的个体越容易生存，优秀的基因更容易保留下来。在遗传算法中，需要随机地选择个体进行交叉操作和变异操作。采用轮盘赌方法进行个体选择，是常用也是最简单的选择方法。选择概率定义：

式中，F（x_i）表示个体x_i的适应度函数值；n表示种群的个体数目；p（x_i）∈（0，1）；从某种意义上而言，个体适应度值越高，对应的选择概率就越大。

（4）交叉。连续优化常见的交叉操作有均匀交叉、模拟二进制交叉、单点交叉和两点交叉等。如何设计实现交叉操作往往和研究的问题有关。

（5）均匀交叉。根据概率来交叉两个父代染色体个体，过程是首先随机产生一个和父代染色体个体同样长度的二进制串，过程中用0来表示不交换，1表示交换，即用这个二进制串作为交叉模板，如图6-10所示。然后再依据模板来对父代两个个体进行交叉操作，最后重新得到两个新个体。

图6-10　均匀交叉

（6）模拟二进制交叉（SBX）。针对两个实数编码的父代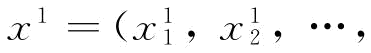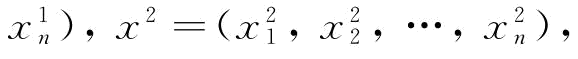被选中的基因则按照如下的方法进行操作。

式中

式中，u是[0，1]区间均匀分布的随机数。

（7）变异。变异是进化策略产生新个体的主要方法，是对群体中个体的某些基因值作变动。对采用二进制编码的染色体，变异是把一些基因值取反，即0变为1，1变为0。遗传算法的基本流程图如6-11所示。

图6-11　遗传算法基本框架