传统的优化方法不能直接解决多目标优化问题，多目标问题的解决常采用加权法、约束法等转化成单目标优化问题。其中进化算法中的群体搜索策略为多目标优化问题的解决提供了合适的方案。由于多目标优化问题中多个目标间相互矛盾，不能同时达到最优解，不同的决策者会根据自己的偏好需求不同，得到不同的最优解。一般把多目标优化问题的所有可能最优解称为非劣解，也称为pareto最优解。

1. 多目标函数优化问题

在对实际问题进行优化时，大部分问题常常涉及多目标优化的情况。与单目标优化问题相比，多目标优化的特点是使各个目标能够达到综合的最优值。但是在多目标优化问题中，各个目标是相互影响的，很难同时达到最优，所以一般适用单目标问题的求解方法就很难用于求解多目标问题。对多目标函数优化问题的数学模型可以表示为

g_i（x）≤0，i=1，2，…，I

h_k（x）=0，k=1，2，…，K

x∈D

式中，g_i（x）和h_k（x）分别为不等式约束和等式约束；x=（x₁，x₂，…，x_D）是一个D维的决策变量。在对多目标优化处理过程中常会涉及以下两个概念。一是可行解，即对于一个x∈D，若x满足优化问题中的约束条件，则称x是优化问题的可行解。二是可行解集，由决策空间D中的所有可行解组成的解集称为可行解集，记为X_f, f是优化多目标函数。

2. 多目标最优解概念

在实际问题中常常需要同时优化多个目标，并且目标之间又存在相互冲突的问题。如果只考虑一个目标值的话，就不能对相应方案的优劣做出判断。因此，对多目标优化中产生了帕累托最优解集概念。

（1）支配解。假设有K个需要最小化的目标值（f₁，f₂，…，f_k），x与y为两组解向量，如果对所有k=1，2，…，K有f_k（x）≤f_k（y），则称解向量x支配（或占优），记做x＜y。(www.daowen.com)

（2）帕累托最优概念。如果解向量x^∗不受任何其他可行解支配，则x^∗称为帕累托最优或者非支配解，且f（x^∗）=[f₁（x^∗），f₂（x^∗），…，f_k（x^∗）]称为非支配解向量。

3. 多目标的处理方法

当时间、碳排放、运输成本权重相同时，目标函数变为min[T（ϕ），E（ϕ），Z（ϕ）]。若货主对时间要求最少，则相应的运输成本将会增加；若要降低运输成本，则货物运输的及时性得不到保障；在低碳运输的背景下，还要考虑到如何降低能源消耗，降低对环境的影响，用来权衡运输方式选择的有效性。因此，当三个目标同时进行考虑时，所得到的解非最优解，存在“效益背反”现象，而需要对三个目标提出某种折中判定，得到相对最优解。

第一步：求单目标的两个端点。求解三个单目标的最小、最大值模型如下：

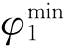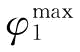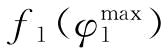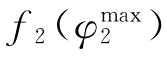假设是模型式（6-33）的最优解方案，则是货物运输的最短运输时间；设是模型式（6-34）的最优解方案，则是货物运输的最长运输时间；设是模型式（6-35）的最优解方案，则是货物运输的最小成本；设是模型式（6-36）的最优解方案，则是货物运输最大成本；设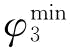是模型式（6-37）的最优解方案，则是货物运输过程的最低碳排放；设是模型式（6-38）的最优解方案，则是货物运输过程的最高碳排放量。

第二步：采用标准0~1区间变换。由于运输时间、运输成本、碳排放三个目标具有不一样的量纲，采用如下公式处理该三个目标：

第三步：根据各目标重要性，动态赋予权重，一般来说，根据行业专家和学者的知识及经验赋予优化目标的权重系数。设给定三个目标的权重分别为w₁、w₂、w₃，其中w₁≥0，w₂≥0，w₃≥0，且w₁+w₂+w₃=1。

第四步：将上述多目标函数求解转化为单目标模型。由于三个目标函数相互间具有矛盾性，只能找到模型的Pareto最优解，因此用加权求和法将多目标函数化成单目标进行求解。