1. 非劣解
中欧班列节点站运输网络优化模型属于多目标规划模型，多目标规划问题一般分为两类求解方法：一种是化多为少的方法，即把多目标化为比较容易求解的单目标或双目标，如主要目标法、线性加权法、理想点法等；另一种是分层序列法，即把目标按其重要性给出一个序列，每次都在前一目标最优解集内求下一个目标最优解，直到求出共同的最优解。
任何多目标规划问题，都由两个基本部分组成：两个以上的目标函数、若干个约束条件。
对于多目标规划问题，可以将其数学模型一般地描写为如下形式：
s.t.
式中，X=[x1，x2，…，xk]T为决策变量矩阵。缩写形式：
s.t.
式（5-18）表示k维函数变量，k是目标函数的个数；式（5-19）中，Φ（X）为m维函数变量，G为m维常数变量，m是约束方程的个数。记可行域为D。
多目标规划问题一般得不到绝对最优解，即不能得到满足各目标的同时最优解，所以多目标问题的求解不能只追求一个目标的最优化，而不顾其他目标，当绝对最优解不存在时，需要引入新的概念——非劣解。
非劣解是指在所给的可供选择的方案集中，已找不到使每一指标都能改进的解，即F（X）为多目标决策问题向量目标函数，fj（X）其分量，对X∗∈D，若在D中不存在X，使得fj（X）＜fj（X∗），则称X∗为向量优化问题的非劣解。
在图5-7中，max（f1，f2），就方案1和2来说，方案1中，f2目标值比方案2大，但其目标值f1比方案2中小，因此无法确定这两个方案的优与劣。在各个方案之间，显然：方案4比方案1好，方案5比方案4好，方案6比方案2好，方案7比方案3好。而对于方案5、方案6、方案7之间则无法确定优劣，而且又没有比它们更好的其他方案，所以它们就被称为多目标规划问题的非劣解。
图5-7 非劣解
2. 化多为少法
1）主要目标法
主要目标法的思想就是抓住主要目标，兼顾其他要求。求解时从多目标中选择一个目标作为主要目标，而其他目标只需满足一定要求即可。因此，可将这些目标转化为约束条件，即利用约束条件的形式来保证其他目标不致太差。这样处理后就转变为单目标优化问题。
对于多目标规划，求解时可以从多目标函数中选择fl（X）作为主要目标，则问题变为
s.t.
2）线性加权法
线性加权法又称为加权组合法或加权因子法，即在将各个分目标函数组合为总的“统一目标函数”的过程中，引入加权因子，以平衡各指标及各分目标间的相对重要性以及他们在量纲和量级上的差异，因此，原目标函数可写为
s.t.
式中，wl是第l个分目标函数的加权因子，其值取决于各目标的数量级及重要程度。
线性加权法需要注意4点。
（1）线性加权之前，各目标应进行无量纲处理：
式中，
为无量纲处理后的结果；flmin（X）、flmax（X）为fl（X）在约束条件下的极小值和极大值。(www.daowen.com)
（2）加权因子归一化要求。线性加权法要求各目标的加权因子和为1，即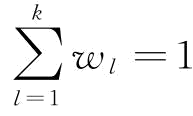
。
（3）加权因子非负要求。加权因子不为负数，即wl≥0。
（4）加权因子的确定。加权因子可以根据设计经验直接给出，有时也可按下式计算得到加权因子：
3）理想点法
理想点法的原理是将多目标规划问题转换为单目标规划问题，求各目标的目标值与其理想值“距离”的最小值的总和，等价于目标值网络与理想值网络的“距离”总和的最小值，寻求最接近完全最优解的有效解。
s.t.
式中，为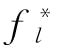
表示第l个目标函数的理想值。
在考虑几个目标的重要度差别情况下，可以再引入加权因子，则构成如下单目标优化问题：
s.t.
式中，wl是第l个分目标函数的加权因子。求解上述问题得到的设计方案既考虑了目标函数的重要性，又最接近完全最优解，因此，它是原多目标优化问题的一个更加理想、更加切合实际的相对最优解。
3. 分层序列法
分层序列法的原理是首先确定各目标的重要性和优先级，并按照重要程度逐一排序，然后依次对各目标函数求最优解，且后一目标应在前一目标最优解域内求解。
设目标函数的重要程度排序为φz（X），z=1，2，…，k，首先对第一个目标函数求解，得到
s.t.
式（5-32）表示第一目标函数最优值，式（5-33）表示第一目标函数最优解。
在第一个目标函数的最优解域中，求第二个目标函数的最优解，即
式（5-34）表示第二个目标函数最优值，式（5-35）表示在第一目标函数最优解域内的第二目标函数最优解。依此方法计算，直到得到第k个目标函数的最优解即为多目标优化问题的最优解。
分层序列法在求解的过程中，若前一目标函数存在唯一最优解，求解将会中断。为了避免前k-1个目标函数中存在唯一最优解而导致计算中断，因此引入目标容差ξ，即宽容分层序列法。
首先对第一个目标函数求最优值：
s.t.
在第一个目标函数的最优解容差域中，求第二个目标函数的最优解，即
依此方法计算，直到得到第k个目标函数的最优解即为多目标优化问题的最优解。式中，ξl为第l目标的最优解容差，一般可以表示为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
