1. 协同优化模型

1）原始模型表达

协同优化最基本的模型原理是将一个复杂的目标函数分解成简单的子目标函数，然后再将这些子目标函数进行协同优化。具体说来，协同优化是在优化每一子目标函数，同时综合考虑其他子目标函数的结果，使子目标函数之间的优化结果能够一致。优化结果一致是指使每一变量的值在每一子目标函数的优化结果中能够一致。一般来说，可以证明，如果变量的值一致，则为最优解。协同优化算法没有局部最优问题，同时具有非常良好的收敛特性。它很好地解决了许多实际问题中非线性优化及组合优化的难题。

如果目标函数是一个含有n个变量的函数E（x₁，x₂，…，x_n），简写成E（x），协同优化算法先将它分解成n个简单的子目标函数：

如果单独优化每一子目标函数，则它们的结果很难达到一致。例如，变量x_i在包含它的子目标函数中的最优解很难相同。对于i=1，2，…，n，如果我们取E_i（x）的最优解中x_i的值作为该变量的值，表示成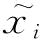，即

式中，X_i是E_i（x）的变量集；X_i\x_i指变量集x_i除去元素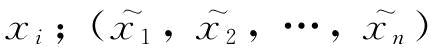则很难为原目标函数E（x）的最优解。

为了使子目标函数之间的优化结果能够一致，协同优化算法在优化每一子目标函数E_i（x）时，同时考虑其他子目标函数的结果，即

具体做法是利用其他子目标函数的优化结果，通过数值加权修正每一个子目标函数，即

式中，λ_k、ω_ij为加权系数，满足0≤λ_k, ω_ij≤1。

然后对修正后的子目标函数进行优化，优化结果再迭代放入修正的子目标函数中。协同优化算法的迭代方程为

协同优化结果使每一变量的值在每一子目标函数的优化结果中达到一致。如果一致，则子目标函数的值就是最优解。

2）标准模型表达

大多数协同优化模型采用两层优化设计方法，与以博弈论为基础的双层规划模型类似，将原始的多学科优化框架划分成顶层和底层：顶层为系统优化控制级，负责向各学科分配系统级状态变量的目标值；底层为并行分布的多个学科子系统，除了满足自身的约束条件，其目标函数为各个子系统的系统层之间的耦合状态变量差最小。子系统经过优化后，各子系统级目标函数反馈到系统级，构成系统级的一致性约束，通过系统级优化来解决各子系统的系统级状态变量不协调的问题，多次迭代后达到整个优化系统的协调。协同优化模型表达如下。

协同优化方法的顶层优化：

式中，F为系统级目标函数，又是整个系统的优化目标函数；Z为系统级优化设计向量；z_j表示第j个系统级设计变量；s_i为学科i的设计变量数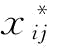；表示学科i的第j个设计变量的优化结果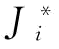；是子空间i的一致性约束；N为子学科数。(www.daowen.com)

协同优化方法的底层优化：

式中，x_i为学科级i的设计变量；s_i为学科i的设计变量数；x_ij表示学科i的第j个设计变量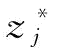；为系统分配给学科级的第j个设计变量期望值；c_i（x_i）为学科级约束。

然而，协同优化模型这种二级优化结构在实践中产生了相应的计算困难，这主要是协同优化方法的数学表达造成的。协同优化方法在系统级优化中加入了二次学科一致性等式约束，从而使原问题的非线性程度加强；系统层优化时，拉格朗日乘子可能不存在，或者是最优点处的约束梯度不连续，导致系统层优化问题无法满足标准Kuhn—Tucker条件；此外，由于系统级一致性约束函数与设计变量没有直接关系，导致系统约束函数可能是非光滑的，甚至是不连续的，而且还可能产生局部最优点，从而带来了协同优化方法的计算耗费大、鲁棒性差等不足。

2. 协同优化模型的改进以及求解方法

由于协同优化标准模型存在计算困难等问题，导致其在实际案例操作中难以应用，因此需要在分析协同优化算法计算困难的原因的基础上，对协同优化算法进行改进研究。

首先列出标准协同优化模型存在问题：

（1）标准协同优化模型中存在两级模型，增加了原问题的非线性程度。

（2）两级模型中存在系统和子系统的相互制约，系统级优化中的一致性等式约束难以满足，一致性等式约束形式可能造成系统级优化的可行域不存在。

目前，已有许多学者对协同优化方法进行了改进研究。Braun等基于罚函数法且引入松弛因子对协同优化标准模型进行改进；Alexandeov等以引入松弛因子为基础，应用分布式分析优化法对标准模型进行改进；Sobieski等提出了使用响应面技术改进协同优化算法的措施。本节通过对上述文献的研究，简单总结了改进的协同优化模型，改进后的模型保留了原模型的特点，即系统级和子系统级可各自寻找最优解也可相互制约协同达到平衡最优解。同时改进后模型以新的方法克服了本身计算困难的问题。

改进子系统级一致性约束，底层优化如下：

改进模型是应用松弛因子法对子系统中的约束进行改进，通过引用松弛变量，将子系统中的等式约束转换成不等式约束。

增加罚函数改进，顶层优化：

式中，γ^（k）表示惩罚因子，优化过程中会随迭代次数的变化而不断变化；N为学科数目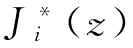；表示第i个系统的目标函数值。

根据上述对标准协同优化算法的改进，降低了模型的求解难度，增大了目标函数解的收敛概率，综合提升了协同优化算法的性能，使协同优化方法在各领域的应用更具有实际意义。