城市综合实力是城市经济、社会、科技等多方面的综合体现，充分反映了城市的影响力、科技创新等。因此对城市进行综合实力评价时，评价指标应遵循完备性、功能性、可获取性等基本原则。结合研究内容，本书从经济发展水平、经济结构、城市规模、交通运输4个方面选取了11个指标，构建了城市综合实力评价指标体系（见图4-3）。

图4-3　城市综合实力评价指标体系

综合评价体系的评价方法主要有层次分析法、灰色综合评价法和主成分分析法。

1. 层次分析法

层次分析法在20世纪70年代中期，由运筹学家萨蒂提出并运用，是以解决多目标复杂问题为基础的定性与定量相结合的决策方法。首先将决策问题依据问题性质、总目标等方面分解成多层次结构模型，接着运用求解正反比矩阵特征向量的方法，得出每一层次的每一个元素对上一层次某个元素的优先权重，最终运用加权和的办法，得到每一个备选方案对总目标的最终权重，结果中权重最大的方案即作为最优方案。具体步骤如图4-4所示。

图4-4　层次分析法计算步骤

2. 灰色综合评价法

灰色综合评价法指的是以专家评判为基础，灰色关联分析理论为指导的综合性评价方法。

具体计算步骤如下。

（1）收集所需评价的数据后，设有n个评价对象，形成矩阵X：X=[X_ij]_m×n，其中i=1，2，…，m, j=1，2，…，n。

（2）确定最优指标集，以各指标的最优值或者最劣值构成参考数据列，记做。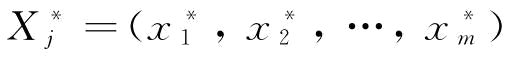

（3）计算关联系数，将X_ij作为比较数据列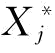，作为参考数据列，带入式（4-1）：

式中，ρ为分辨系数，在（0，1）中取值，得灰色评判矩阵E=[ξ_i（j）]_m×n。(www.daowen.com)

（4）计算综合评判结果。设W=（w₁，w₂，…，w_n）为n个评判指标的权重分配矩阵，其中w_j（j=1，2，…，n）作为第j个评判指标权重，综合评判结果矩阵式为

（5）根据每个观察对象的关联系数，进行综合评价。

3. 主成分分析法

主成分分析法又称主分量分析，旨在利用降维的思想将多种指标转化为较少的几个新综合指标。这些新指标之间互不关联，但能综合反映原来多种指标的信息，被称为原来指标的主成分。该方法通过原始数据初始化后，依次得出相关系数矩阵、特征根、特征向量等。

基于主成分分析法的城市综合实力评价步骤如下。

第一步：收集所需城市的指标数据，然后依照行排列组成矩阵Z。

第二步：对原始数据进行标准化处理，其中均值取0，方差取1，从而得到标准化矩阵X。

第三步：由标准化矩阵X求相关系数矩阵A。

第四步：根据相关矩阵A的特征方程得出特征根以及所对应的特征向量，并按由大到小的顺序进行排列，从而计算累计贡献率。

第五步：若累计贡献率大于85%，由此得出主成分个数m以及结果矩阵T。

为了更加迅速准确地获得数据，本书中结合SPSS软件依照主成分分析法的步骤进行计算。SPSS软件集数据录入、整理以及分析功能于一身，客户能够根据实际需求选择模块求解。运用SPSS软件做主成分分析法的步骤如图4-5所示。

图4-5　基于主成分分析法的SPSS软件运用