1. 随机Petri网基本理论

基本的Petri网结构简单，主要包含元素有以下几种。

库所（Place）：用“○”表示，也称P元素，表示系统的位置、状态，每个圆圈中可以存放一定的资源。

变迁（Transition）：用“□”表示，也称T元素，指系统中资源的消耗、使用和产生。

有向弧（Connection）：用“→”表示。

图3-6　Petri网模型

托肯（Token）：用“●”表示，能在两个库所之间移动，个数代表库所中资源的数量。如图3-6所示，库所P_i中的“托肯”数量为1。

一个基本的Petri网定义为一个六元组，即有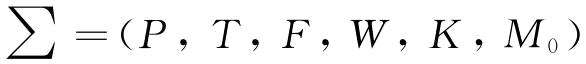，其中：

P={P₁，P₂，…，P_m}是有限库存（Place）的集合；

T={T₁，T₂，…，T_n}是有限变迁（Transition）的集合；

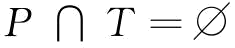，是指集合P和集合T相交；

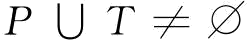，是指集合P和集合T不同时为空集；

F⊆（P×T）∪（T×P）（×为笛卡尔积），意为关系F只存在于集合P和集合T之间，即有向弧集合；

W:F→{1，2，…}（关系集合F是到正整数的映射）是有向弧的权函数，集节点流关系集合；

K:P→{1，2，…}（集合P到正整数的映射）是库所的容量函数；(www.daowen.com)

M₀:P→{1，2，…}（集合P到自然数的映射）是初始标识。

图3-6中Petri网的状态标识M=[1，0，0，0]。如果为起始状态，则M₀=[1，0，0，0]。

2. 基于Petri网的工作流程模型基本结构

串行结构：只有一条没有任何分支的通路，可以用来描述一系列以不变的顺序依次执行的活动。如图3-7所示，在串行结构中，库所与变迁顺次执行，托肯由P₁经过T₁的激活传递给P₂，然后又通过T₂的激活传递给P₃，依次顺序进行。

图3-7　串行结构

并行结构：表示的是几个事件可以同时进行，并且这些事件之间是互不影响的，每个分支的变迁激活不会使其他分支的变迁被激活。在这些分支都完成之后，才会进行后续的事件。如图3-8所示，托肯由P₁经过变迁T₁的激活转移到P₂与P₄中去，然后T₂与T₃都被激活，T₄才被激活，托肯从P₃与P₅转移到P₆中去。

图3-8　并行结构

循环结构：用来描述一些需重复执行的活动，如图3-9所示。

图3-9　循环结构

选择结构：用来描述两个任务的执行必须是二选一的分支活动。如图3-10所示，T₁被激活之后，托肯由P₁转移到了P₂中，接下来T₂和T₃只能二选一，无论哪个变迁激活之后，托肯又会转移到P₃中，接下来就是串行结构。

图3-10　选择结构

3. 集装箱运输业务流程Petri网的模型构建

在对集装箱业务流程Petri网模型的构建上，需要先确定其对应基本Petri网的五大要素，定义的五元组如下：

式中，P是元素集，代表库所，表示集装箱运输开始或结束的结点，以及信息、单证流转的结点、部门；T是变迁集，代表变迁，表示集装箱运输过程中的信息传递或单证处理；F是P和T之间的关系；A是流程的属性，表示集装箱运输过程中活动时间及成本的变量；M₀是初始标识，表示在初始条件下各个库所的托肯分布，即集装箱量。