列车-线路是一个动态相互作用系统，而轮轨关系是车辆子系统、轨道子系统的联系纽带。前面推导的车辆运动方程、轨道运动方程中，只要确定了轮轨相互作用力，应用数值积分方法，通过编制计算程序就可以进行车辆-轨道系统的动力学仿真分析。

1）轮轨接触几何关系

轮轨接触几何关系是准确计算轮轨法向力和蠕滑力的前提和基础。当不考虑轮对摇头运动时，轮轨接触几何参数是平面问题，轮轨各接触几何参数仅是轮对中心横移量的函数。但当车轮存在摇头运动的情况下，轮轨接触几何参数扩展成空间问题，其空间搜索接触点的计算效率很低。王开文对此提出了一种求解轮轨空间接触的一维搜索算法。其基本原理是轮轨空间接触点只可能在一条空间曲线上（这条曲线称为迹线），可以通过寻求一条迹线来代替整个踏面区域，从而利用迹线在一维区域（空间曲线）扫描以代替在二维区域内扫描，这样可以大大降低计算工作量。图8-8为轮轨空间接触示意图。

在图8-8中，按触点C在三个面之内，即包含O2点的滚动圆平面，以O2为球心、以Rw（车轮滚动圆半径）为半径的球面，O1O′1C′-C平面。通过三个面的方程可推导得到轮轨接触点C在绝对坐标系中的坐标：

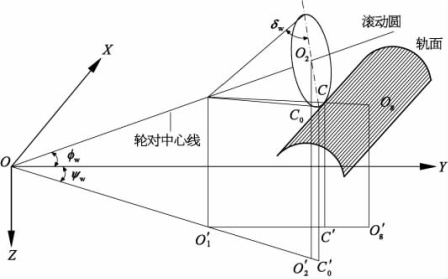
图8-8　轮轨空间接触几何关系示意图

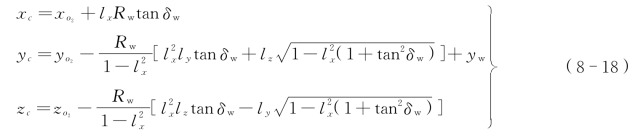
式中 lx、ly、lz——X、Y、Z方向的余弦，lx=-cosφw sinψw，ly=cosφw cosψw，lz=sinφw；

xo2、yo2、zo2——车轮滚动圆圆心O2坐标，xo2=dw lx，yo2=dw ly+Yw，zo2=dw lz；

Rw、δw——车轮滚动圆半径、车轮踏面接触角；

φw、ψw、yw——轮对侧滚角、摇头角、横向位移；

dw——轮对坐标系中车轮踏面各滚动圆的横向坐标。

因此当轮对横向位移、摇头角、侧滚角一定时，通过逐步改变轮对坐标系下车轮踏面各滚动圆横坐标dw，就可以构成某时刻的轮轨空间接触迹线。轮轨接触点的计算受到轨对及钢轨的运动位移量和轨道不平顺值，因此每一时刻均需重新计算轮轨接触点。

2）轮轨法向力计算

传统轮轨力的求解是通过忽略轮对的垂向和侧滚惯性力，由轮对运动平衡方程迭代得到。为避免这一迭代过程，采用著名的赫兹非线性弹性接触理论计算轮轨法向力。

根据某时刻轮对的横向位移、摇头角、侧滚角、钢轨的横向位移、垂向位移、扭转角和轨道不平顺，按照前述轮轨接触点的计算方法，可以求得该时刻左右轮轨间的垂向相对位移，然后减去零时刻左右轮轨间的垂向相对位移。将垂向相对位移向轮轨接触点的法向进行投影，就可得到左右侧轮轨间的法向压缩量，即

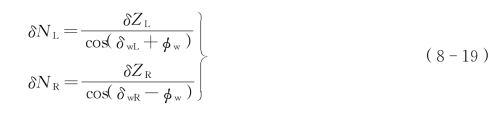
式中 δwL、δwR、φw——左右车轮踏面的接触角、轮对侧滚角；

δZL、δZR——左右侧接触点处的轮轨垂向相对位移；

δNL、δNR——左右侧轮轨间的法向压缩量。

应用赫兹非线性弹性接触理论，可以确定轮轨之间的垂向作用力：

式中 R——车轮滚动圆半径；

δN（t）——轮轨接触点的法向弹性压缩量；

G——轮轨接触常数，对锥形踏面来说，G=4.57R-0.149×10-8（m／N2／3），对磨耗型踏面来说，G=3.86R-0.115×10-8（m／N2／3）。

3）轮轨蠕滑力计算

轮对在轨道上滚动时，轮轨间将产生相对位移和速度差，轮轨接触斑金属表层不仅有微量弹性变形，还含有微量的速度差，这种金属材料的微量弹性滑动称为蠕滑。车轮与钢轨间的滑动将产生两者之间的速度差，车轮与钢轨两紧压着的弹性体之间将形成接触斑。由于摩擦的存在，车轮与钢轨在接触斑上会产生蠕滑力。

关于轮轨蠕滑力的计算，先以Kalker的线性蠕滑理论计算，考虑到车辆运行中，轮轨间蠕滑有可能达到饱和，所以利用Shen-Hedrick-Elkins理论进行非线性修正。(www.daowen.com)

以轮轨接触椭圆中心C为原点，建立轮轨接触斑坐标系C-e1e2e3，如图8-9所示（以右侧轮轨接触点为例）。e1轴和X轴重合，为车轮的前进方向；e2轴位于轮轨接触平面内，它与Y轴的夹角在左侧接触点为δL+φ，在右侧轮轨接触点为δR-φ；e3轴为轮轨接触平面法向。

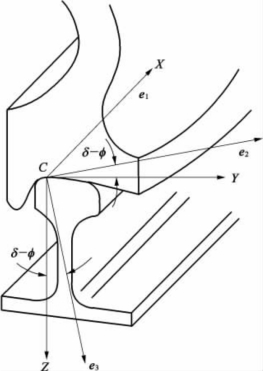
图8-9　右侧轮轨接触示意图

设接触斑坐标系中，车轮踏面上的接触椭圆沿e1轴、e2轴和绕e3轴的运动速度分别为Vw1、Vw2和Ωw3；钢轨上接触椭圆的运动速度分别为Vr1、Vr2和Ωr3，则轮轨蠕滑率在接触斑坐标系中可定义为

式中 V——轮对在钢轨上的名义前进速度。

根据Kalker线性蠕滑理论，由于蠕滑产生的蠕滑力和蠕滑力矩的大小与蠕滑率成正比且方向相反，即

式中 Fx、Fy——纵向、横向蠕滑力；

Mz——旋转蠕滑力矩；

f11、f22——纵向、横向蠕滑系数；

f23——旋转／横向蠕滑系数；

f33——旋转蠕滑系数。

蠕滑系数由下式确定：

其中 G——轮、轨材料的合成剪切模量，

a、b——接触椭圆的长半轴和短半轴；

Cij——Kalker系数。

Kalker线性蠕滑理论只适用于小蠕滑率和小自旋的情形，即轮轨接触面主要由黏着区控制的情形。对于轮轨接触面主要由滑动区控制的大蠕滑率、大自旋甚至完全滑动的情况，蠕滑力与蠕滑率之间呈非线性关系，甚至趋于滑动摩擦力这一饱和极限。为此，采用沈氏理论做非线性修正，使蠕滑力的计算可以广泛适用于任意蠕滑率值的情形，从而适应轮轨相互作用的实际工况仿真计算。

将纵向蠕滑力Fx和横向蠕滑力Fy合成为

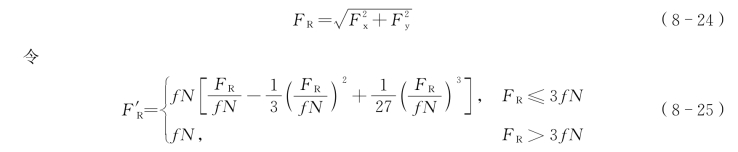
式中 f——轮轨间的摩擦系数；

N——轮轨接触的总法向力。

引入修正系数ε：

则可以得到修正后的蠕滑力和蠕滑力矩：