1）主梁节段模型静力三分力试验

主梁节段模型静力三分力试验的目的是测量桁梁及车体各自的静力三分力系数，为风致响应计算分析及考虑风载的车桥耦合振动分析提供气动力参数。

综合考虑主梁的宽度、高度及风洞试验段的大小，桥梁和车辆节段模型均采用1∶60.14的几何缩尺比。根据主梁的断面形式制作了节段模型，桥梁模型长2.095 m，宽0.766 m（实桥宽46.0 m），高0.266 m（实桥高16.0 m），长宽比L／B=2.73＞2，满足《公路桥梁抗风设计规范》的要求。模型采用环氧树脂板和优质木材制作，对于成桥状态，栏杆的透风率取为55.9%。

由于该桥铁路为客运专线，风洞模型试验列车节段模型取和谐号CRH2。CRH2列车模型的尺寸为长2.095 m，宽0.056 2 m（实车宽度3.38 m），高0.058 2 m（实车高度3.5 m，未包括车轮）。

施工状态节段模型照片如图7-21所示，成桥状态节段模型照片如图7-22所示。试验在西南交通大学单回流串联双试验段工业风洞（XNJD-1）第二试验段中进行。

图7-21　施工状态节段模型照片

图7-22　成桥状态节段模型照片

主桁梁节段模型三分力系数的测量共进行了以下几种状态的试验：施工状态、成桥无车状态和桥有车状态。试验来流为均匀流。

图7-23给出了该桥成桥无车状态在体轴坐标系下、风轴坐标系下的静力三分力系数随攻角的变化关系曲线；图7-24给出了该桥施工状态在体轴坐标系下、风轴坐标系下的静力三分力系数随攻角的变化关系曲线。

可以看出，在α=0°的情况下，成桥无车状态时的阻力系数为0.873 2；施工状态时为0.767。

成桥无车状态升力系数曲线（CL-α）和力矩系数曲线（CM-α）的斜率在较大的正、负攻角（-12°～5°）范围内均为正值；施工状态升力系数曲线（CL-α）和力矩系数曲线（CM-α）的斜率在较大的正、负攻角（-12°～7°）范围内均为正值，这说明主梁断面具备气动稳定的必要条件。

考虑到列车可能在桥上不同线上均有可能出现，为了测量出列车在不同线上时的三分力系数，特对五峰山长江大桥四铁路线进行编号说明，从上风侧至下风侧分为1、2、3、4线。

桥上有车状态理论上可能存在单线有车、双线有车，本试验针对单线有车、双线有车状态分别进行静力系数测量试验。试验结果参见文献［16］。

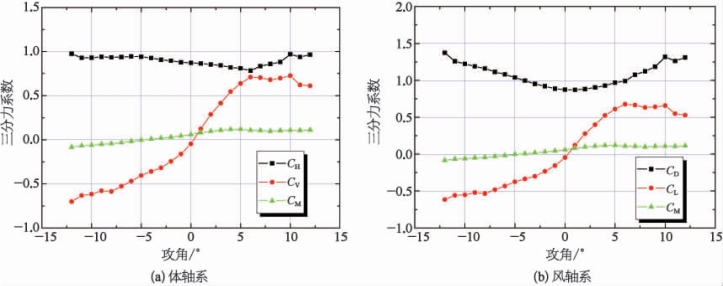
图7-23　成桥无车状态主桁梁三分力系数

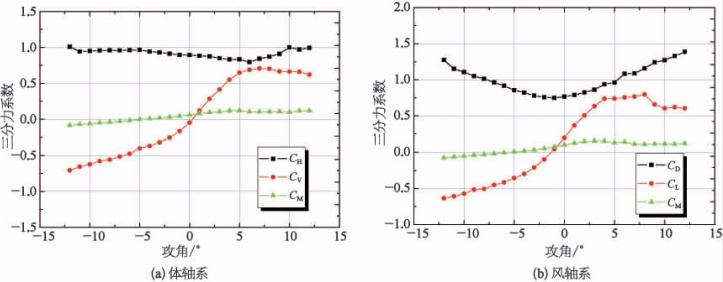
图7-24　施工状态下桁梁三分力系数

试验结果表明，车辆位于1线时较2线的阻力系数大；双车行驶时，由于1线的遮风效应，2线车气动阻力显著减小。另外，桥梁、车辆内三分力系数在不同组合状态下相互差异均较大，这表明车辆和桥梁之间相互的气动影响非常明显。

列车在桥上运行对主桁梁的风参数有较大影响，考虑列车后车、桥总体所受的风载有较大增加，但主桁梁本身的风载则减少；另外，列车在不同线上运营时对车、桥总体所受的风载略有影响。具体表现在如下方面：

（1）单线有车状态。列车在1线上运营时所受的风荷载最大，在其他线上运行时风荷载相对较小，因而对于单线有车状态，列车在1线上运行为最不利状态。

（2）双线有车状态。由于遮挡效应，上风侧线上的列车所受风载大于下风侧列车所受风载。且两车相距越近（相邻线），遮挡效应越明显，即下风侧车所受的风载越小。这说明如在桥上发生相邻线双车交会，下风侧的列车所受的风载会有较大突变，这对行车较为不利［16］。

2）主梁节段模型颤振试验(www.daowen.com)

试验目的是通过节段模型试验直接测定颤振临界风速，从而对该桥的动力抗风稳定性进行初步评估。试验在西南交通大学XNJD-1工业风洞第二试验段中进行。置于风洞中的动力试验模型（成桥无车状态）如图7-25所示。

图7-25　置于风洞中的动力试验模型（成桥无车状态）

颤振试验在均匀流条件下进行。对于成桥状态，分别进行了α=0°，+3°，-3°三种攻角情况下的试验。

试验表明，当节段模型试验模拟的阻尼比取0.44%（小于《公路桥梁抗风设计规范》钢桁架主梁0.5%的规定）时，在攻角为+3°来流风时其颤振临界风速为60.6 m／s，略高于成桥状态相应的颤振检验风速（58.2 m／s）。但当阻尼比取0.62%时，相应+3°攻角下其颤振临界风速为75.5 m／s，远高于成桥状态相应的颤振检验风速（58.2 m／s）。其他攻角下（-3°或0°），主梁发生颤振的临界风速均高于76.3 m／s，均远高于成桥状态相应的颤振检验风速。因而可见，五峰山长江大桥的成桥状态从-3°攻角到+3°攻角时的颤振临界风速均高于相应状态的颤振检验风速（58.2 m／s），同时这说明该桥的颤振稳定性满足要求［14］。

3）主梁节段模型涡激共振试验

试验的目的是通过测定节段模型发生涡激振动的发振风速和振幅，从而对主梁的涡激振动特性进行初步评价。涡激振动是由于气流绕过物体时在物体两侧及尾流中产生周期性脱落的旋涡激励使物体发生的限幅振动，它通常发生在较低的风速下，其振动形式通常为竖向涡振或扭转涡振。

基于人体舒适度及行车安全性的考虑，涡激振动振幅的限制值、主梁涡激振动振幅须小于规定的容许值，其容许值如下：

成桥状态：

主梁竖向涡振振幅容许值　

主梁扭转涡振振幅容许值　

对于成桥状态，分别进行了α=0°，-3°，+3°三种攻角条件下的试验，试验来流为均匀流。

试验表明，对于成桥状态，竖弯阻尼比为0.39%，扭转阻尼比为0.44%时，有如下结果：

（1）风攻角α=0°，-3°时，对于成桥状态，在风速小于80 m／s范围内均没发现有扭转涡振或竖向涡振发生。

（2）风攻角α=+3°时，对于成桥状态，在风速为12～15 m／s范围内发生有竖向涡振，其最大竖向涡振振幅均方根值为0.161 m；相应的最大竖向涡振振幅幅值为0.228 m，小于《公路桥梁抗风设计规范》规定的允许值0.241 m。

（3）风攻角α=+3°时，对于成桥状态，在风速为18～25 m／s范围内发生有较大的扭转涡振，其最大扭转振幅均方根值为0.231°；相应的最大扭转振幅幅值为0.327°，大于《公路桥梁抗风设计规范》规定的允许值0.256°。

对于成桥状态，竖弯阻尼比为0.64%，扭转阻尼比为0.63%时，有如下结果：

（1）风攻角α=0°，-3°时，对于成桥状态，在风速小于80 m／s范围内均没发现有扭转涡振或竖向涡振发生。

（2）风攻角α=+3°时，对于成桥状态，竖弯涡振锁定风速区减小，同时涡振幅值也明显变小，在风速为12～15 m／s范围内发生有竖向涡振，其最大振幅为0.025 m，小于《公路桥梁抗风设计规范》规定的允许值0.241 m。

（3）风攻角α=+3°时，对于成桥状态，扭转涡振锁定风速区减小，同时涡振幅值也明显变小，在风速为20～25 m／s范围内发生有扭转涡振，其最大振幅为0.125°，小于《公路桥梁抗风设计规范》规定的允许值0.256°。当发生最大振幅扭转涡振时，同线铁路两轨道间高差为1 435×0.125×3.141 59／180≈3.1（mm）。

可见，随着阻尼比的提高，主梁发生涡振的锁定风速区会变窄，同时涡振幅值也明显变小，虽然《公路桥梁抗风设计规范》5.4.1条建议钢桥的阻尼比取0.005，但五峰山长江大桥主桥为钢桁主梁混凝土桥塔的悬索桥，同时采用有道砟轨道铁路，参考国内外相关资料，其阻尼比取0.006 5左右进行评价是合适的。基于此，五峰山长江大桥的成桥状态在风攻角α=-3°，0°，+3°下，涡振振幅均小于容许值，因而涡激振动不致发生影响人体舒适度及行车安全性的问题，也不会产生由于风致涡振引起结构的疲劳问题［16］。