1）数值仿真计算原理

把桁架主梁简化为平面模型进行计算分析。将主梁作为质量、弹簧和阻尼系统，建立弯曲和扭转流固耦合数值仿真计算模型。数值仿真计算原理示意如图7-16所示，主梁的竖向振动方程和扭转振动方程分别如式（7-49）和式（7-50）所示：

式中 m——主梁等效质量；

ch、cθ——主梁竖弯阻尼和扭转阻尼；

kh、kθ——主梁等效竖弯刚度和等效扭转刚度；

Fh、Mθ——主梁受到的气动升力和气动力矩；

——主梁竖向位移、速度和加速度；

——主梁扭转位移、速度和加速度。

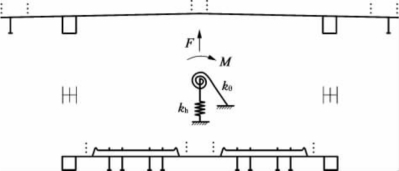
图7-16　数值计算原理示意图

对于不可压缩流体的连续方程和纳维-斯脱克斯方程为［13］

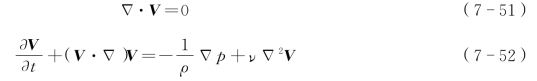
式中 V——流体的速度分量；

ρ——流体密度；

ν——流体运动黏性系数，空气中运动黏性系数常温时取1.5×10-5 m2·s-1。

求解流体方程［式（7-51）、式（7-52）］得到主梁表面的压强，计算主梁受到的升力和力矩；将升力和力矩分别代入主梁振动方程［式（7-49）、式（7-50）］，运用Newmark-β法求解主梁动力响应，将主梁的速度传递给网格，通过动网格技术使主梁运动，然后开始下一个时间步的计算。如此循环进行流固耦合计算得到各时间步的主梁位移。

2）数值仿真计算模型(www.daowen.com)

数值仿真计算参数见表7-8［16］，《公路桥梁抗风设计规范》6.6.1条建议钢桁架主梁的阻尼比取0.005，但五峰山长江大桥主桥为钢桁主梁混凝土桥塔的悬索桥，同时采用有道砟轨道铁路，参考国内外相关资料，其阻尼比取0.006 5左右进行评价是合适的。数值计算参数见表7-8，按照桥梁结构实际尺寸建立模型，主梁数值计算模型如图7-17所示。

表7-8　数值计算参数

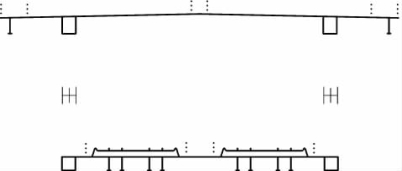
图7-17　数值计算模型

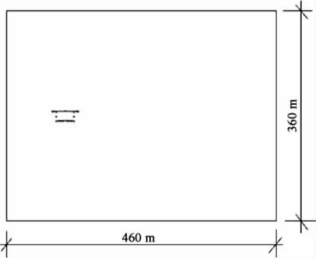
图7-18　数值计算区域

数值计算区域如图7-18所示，计算区域长460 m，宽360 m。数值计算网格如图7-19所示，风向从左至右，左侧设定为速度入口，右侧设定为自由出流。上下边界为无滑移固壁边界。数值计算中，靠近主梁网格加密，远离主梁网格逐渐稀疏，网格总数约8万。采用有限体积法求解，其中压力和速度的耦合采用SIMPLE算法，湍流模型采用LES大涡模型。

图7-19　数值计算网格

3）数值仿真计算结果

主梁旋涡脱落如图7-20所示。

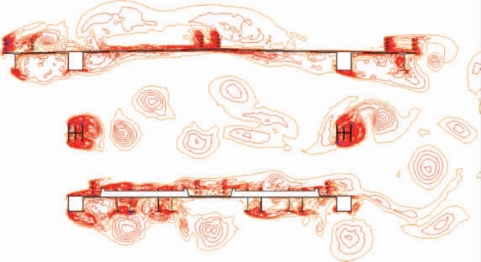
图7-20　旋涡脱落图

数值仿真计算表明该桥无明显颤振发散现象，因此取主梁扭转位移标准差为0.5°时对应的风速作为颤振临界风速。计算结果见表7-9，对于颤振临界风速，数值仿真计算结果和节段模型风洞试验结果吻合较好。在相对不利的+3°风攻角时颤振临界风速为72 m／s，大于数值计算所对应的颤振检验风速62.3 m／s，满足颤振稳定性要求。

表7-9　颤振临界风速