1）计算模型

用Midas Civil建立全桥有限元计算模型，该桥的动力特性分析采用空间结构计算图式，主桁、横梁、平联、主塔等均离散为空间梁单元，上、下桥面正交异性桥面板用板单元模拟，主缆和吊索用索单元模拟。成桥阶段、独塔自立状态的计算模型分别如图7-13和图7-14所示。

图7-13　成桥状态计算模型

图7-14　主塔自立状态计算模型

2）边界条件

本桥成桥状态结构各部位边界条件见表7-4。

表7-4　成桥状态结构各部位边界条件

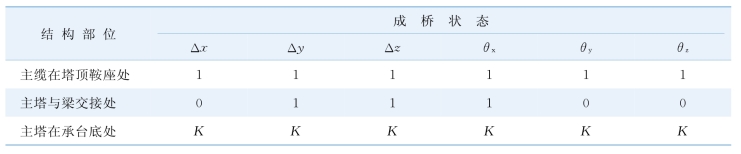
注：Δx、Δy、Δz分别表示沿纵桥向、横桥向、竖桥向的线位移；θx、θy、θz分别表示绕纵桥向、横桥向、竖桥向的转角位移；1表示约束；0表示放松；K为弹性支撑刚度。

3）桥梁动力特性分析

成桥状态的振型主要特点见表7-5，其相应的振型如图7-15所示。

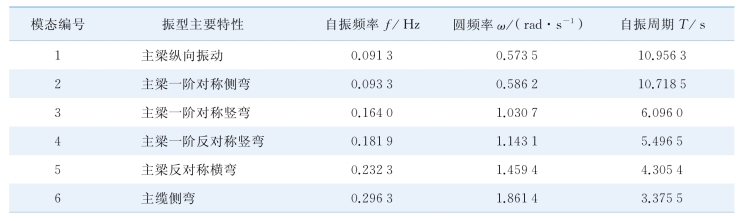
表7-5　成桥状态动力特性

(www.daowen.com)

（续表）

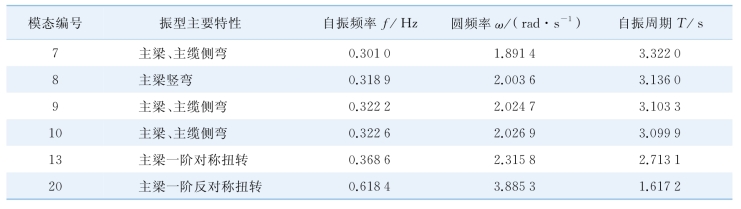
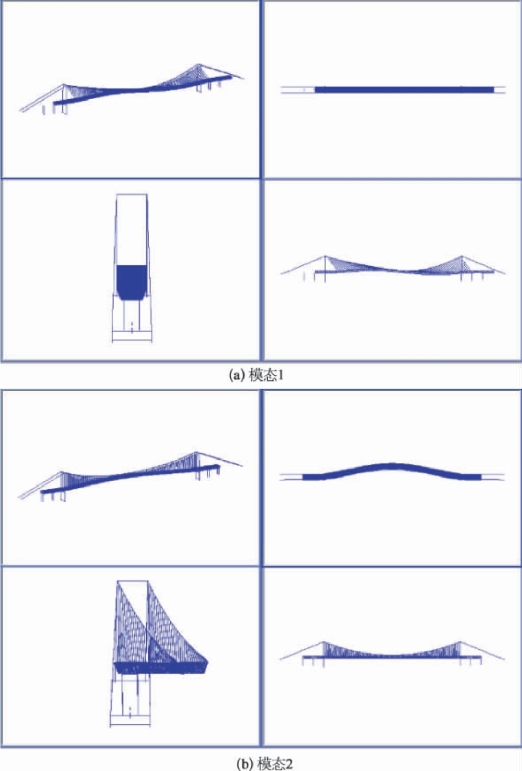
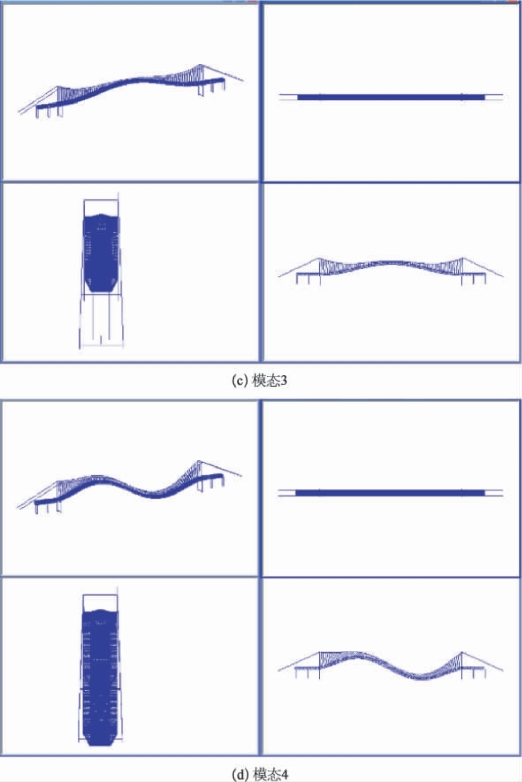
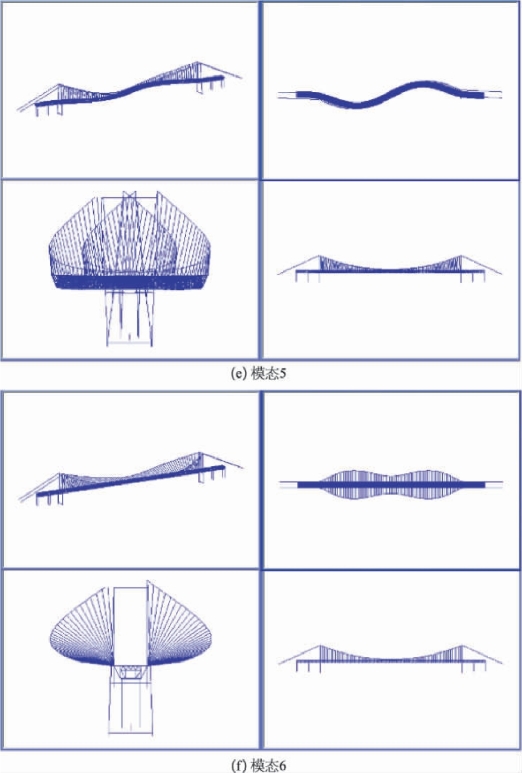
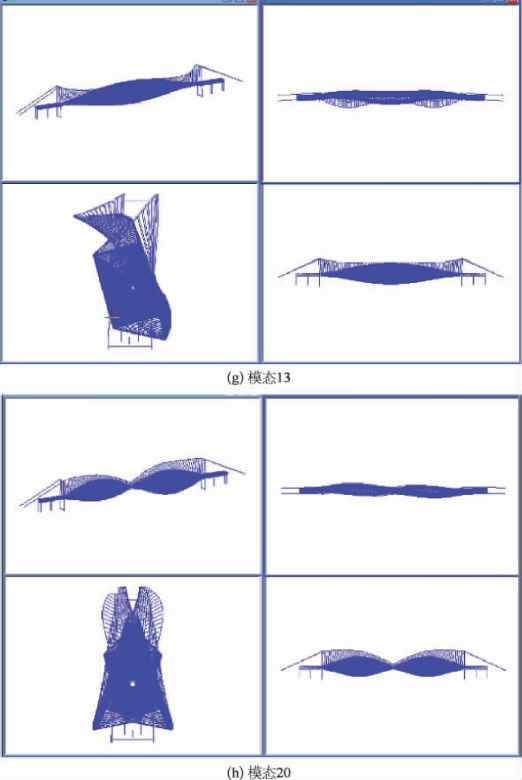
图7-15　成桥状态振型图

从振型图来看，可得：

（1）本桥主跨大，单跨跨度达1 092 m，吊索间距43 m，主梁宽跨比较小，主梁采用半漂浮体系，第一阶出现主梁的纵向振动，第二阶振型出现主梁的侧弯振型。

（2）由于本桥的主梁为钢桁梁，桥面很宽，主梁的扭转刚度较大。该桥正对称扭转振型出现在13阶，f13=0.368 6 Hz，反对称扭转振型出现在20阶，f20=0.618 4 Hz。

（3）由于结构主跨大，相应的周期都很长，这对结构抗震来说是较为有利的。

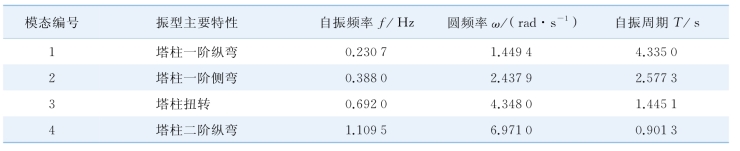
主塔自立状态的振型主要特点见表7-6，由于塔较高，塔柱的纵向刚度较低，表现在振型上为塔的纵弯振型比塔的侧弯振型先出现。

表7-6　主塔自立状态动力特性