桥梁的长大化使其刚度不断下降，导致对风的敏感性不断增加，由于自然风的紊流特性，不可避免地会使大跨柔性桥梁结构发生抖振。风荷载被分解为平均风引起的静风荷载、脉动风引起的抖振力和流固耦合引起的自激力三部分。作用在桥梁主梁上的力可表达为

式中 M、C和K——节段构件的质量、阻尼和刚度矩阵；

X——构件位移运动矢量，包括竖弯、扭转和侧弯三种运动形态；

FG、Fst、Fb和Fse——作用在结构上的重力、静风力、抖振力和自激力。

Davenport抖振力表达式的基本假定是刚性模型假定，即结构本身的振动不会影响风荷载。实际上结构振动与风场会形成一种耦合关系，结构与风场的耦合形式上表现为结构的阻尼特性与刚度特性的改变。

自1971年Scanlan提出了用气动导数表示的自激力模型后，基于气动导数的颤振分析得到了广泛运用。Scanlan自激力模型又被引入大跨度桥梁的抖振分析中，以考虑气动刚度和气动阻尼对抖振的影响。Sarkar和Jones将Scanlan气动力模型加以推广，提出用18个颤振导数表示的气动自激力。静风力采用基于三分力系数的定常表达，抖振力采用基于脉动风速场的Scanlan准定常气动力理论，并引入气动导纳函数修正。自激力采用Lin提出的基于脉冲响应函数的时域表达式，利用Roger有理函数表达桥梁断面非定常气动力传递函数，采用递推方式求解其中的卷积项。

1）静风力

处于风速为U的均匀流中的桥梁主梁，其受到的空气静力作用如图7-12所示，分为升力FV、阻力FH和扭矩MZ。由于体轴坐标系和有限元分析时结构的单元局部坐标系一致，静风荷载可以直接按单元荷载加载到结构上，故采用体轴坐标系计算静风力，体轴坐标系下的单位长度主梁上的静风力表达式如下：

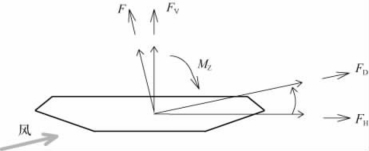
图7-12　作用于桥梁横断面的风荷载

式中 CV（α）、CH（α）、CM（α）——体轴坐标系下攻角为α时的桥梁三分力系数；

ρ——空气密度；

U——来流风速；

B、H——主梁截面的宽度、高度。

2）抖振力

根据Scanlan准定常气动力理论，并引入气动导纳函数修正，作用在单位长度主梁上的抖振力为

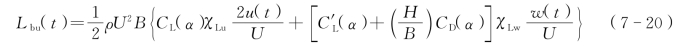
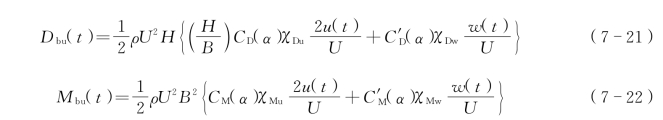
式中 Lbu（t）、Dbu（t）、Mbu（t）——t时刻的抖振升力、抖振阻力、抖振力矩；

ρ、U——空气密度、来流平均风速；(www.daowen.com)

CL（α）、CD（α）、CM（α）——升力系数、阻力系数、力矩系数；

——升力、阻力和力矩系数斜率；

u（t）、w（t）——作用于主梁上的横桥向、竖桥向脉动风速；

χLu、χLw、χDu、χDw、χMu、χMw——时域气动导纳函数。

上式中的三分力系数及其斜率的取值与静力风荷载方法相同。

气动导纳函数是一个修正系数，用来描述气动力的非定常特性，是度量脉动风速到脉动气动力的函数。气动导纳函数是频率的函数，现有的气动导纳表达式系频域表达式，不能直接在时域中使用。为了在时域计算中考虑气动导纳的修正，常用的方法有抖振力谱法和等效风谱法。对抖振力时域表达式做傅里叶变换，抖振力谱如下所示：

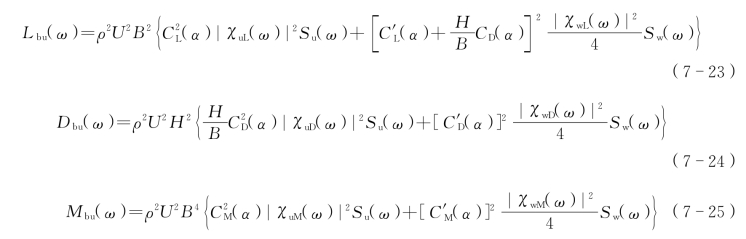
式中 Su（ω）、Sw（ω）——水平和竖向脉动风速的风速谱；

|χuL（ω）|2、|χwL（ω）|2、|χuD（ω）|2、|χwD（ω）|2、|χuM（ω）|2、|χwM（ω）|2——水平和竖

向脉动风速相对抖振升力、阻力和升力矩的气动导纳。

气动导纳函数虽然早在20世纪60年代就已经提出，但由于大跨度桥梁主梁断面一般是钝体形状，其气动导纳函数与其具体形状和湍流特性有关，无法得到理论解，所以桥梁主梁断面的气动导纳函数没有统一表达式。对于流线型的扁平主梁，Sears函数的Liepmann简化形式是一个很好的近似，如下所示：

对于较为钝化的主梁，气动导纳函数可偏安全地取为1.0，即不考虑气动导纳的影响。采用等效风速谱来考虑气动导纳的影响，即

式中 |χ（ω）|2——气动导纳函数。

进行风速时程模拟时，采用等效风速谱这样便可得到等效水平和竖向脉动风速时程u*（t）、w*（t），将其视为脉动风速u（t）和w（t），这样就可得到考虑气动导纳修正后的抖振力。

3）自激力

自1971年Scanlan提出了用气动导数表示的自激力模型后，基于气动导数的颤振分析得到了广泛运用。Sarkar和Jones将Scanlan气动力模型加以推广，提出用18个颤振导数表示的气动自激力公式，如下所示［14］：

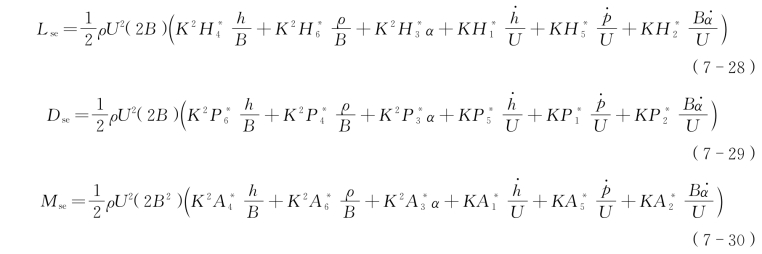
其中，是量纲为1的气动导数，表示力与位移和速度之间的关系，是折算频率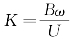的函数，其中B为主梁截面宽度，ω为振动圆频率，U为平均风速，ρ为空气密度。