气动弹性力学是研究弹性体在气流作用下力学行为的一门学科。弹性结构在气动荷载的作用下会产生变形或振动，弹性结构的变形或振动改变了结构的气动构型，进而又会影响作用在弹性结构上的气动荷载的大小和分布。正是由于这种气流与弹性结构的交互作用，使得弹性结构在气流中产生各种各样的气动弹性现象，气动弹性力学本质上是流固耦合问题。桥梁结构的风致振动问题属于气动弹性问题。计算流体力学（computational fluid dynamics，CFD）以计算机作为工具，通过离散化数值方法来求解各种流体力学问题。其中流固耦合（fluid-structure interaction，FSI）计算方法的开发和应用是目前计算流体力学发展的重点领域，虽然流固耦合数值仿真技术在航空、化工、海洋工程等工业领域的应用取得了成功，但由于土木工程中结构体型大、外形多呈钝体，其绕流不可避免地伴随着流动分离，再加上旋涡脱落等复杂的流动现象，因而在建筑结构风工程领域，数值模拟没有达到成熟的地步。流固耦合技术在土木工程中，特别是在桥梁工程中的发展和应用是近30年来的事。相对于风洞试验，数值风洞有以下优点：

（1）桥梁风洞试验一般采用缩尺模型，节段模型一般只有实桥的1／50，全桥气弹模型一般只有实桥的1／120～1／200，不可避免地存在由于缩尺所带来的几何尺寸、弹性参数、惯性参数、重力参数、黏性参数及阻尼参数等相似性问题，相似性问题直接影响着试验精度。而数值模拟能够建立与实际结构尺寸相同的计算模型，克服相似性问题，更真实地模拟实际桥梁结构的风致振动情况。

（2）主梁节段模型风洞试验费用在几十万元，而全桥气弹风洞试验费用高达百万元以上。整个风洞试验过程耗时数月。相对风洞试验数值模拟成本较低，速度较快。数值模拟修改方便，在初步设计阶段，可以先用数值仿真技术进行结构气动性能方案比选，再有针对性地进行风洞试验。一方面能够提高设计效率，降低设计成本；另一方面，两种分析方法的结果可以相互校验，提高设计精度。

（3）风洞试验对于流场显示难度较大，需要专门的设备。数值模拟可以很方便地显示流场形态，展现气流与结构之间的相互作用，这对于研究桥梁结构风致振动的微观机理、指导桥梁结构气动优化设计起到重要的作用。

对于桥梁风致振动计算，可以模拟节段模型风洞试验，将桥梁主梁作为质量、弹簧和阻尼系统，建立弯曲和扭转流固耦合数值仿真计算模型，对颤振、涡激共振和驰振等风致振动现象进行计算分析。数值仿真计算原理示意如图7-11所示，主梁的竖向振动方程和扭转振动方程分别如式（7-12）和式（7-13）所示。

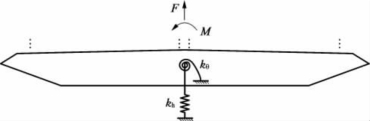
图7-11　数值仿真计算原理示意图

式中 m——主梁等效质量；

ch、cθ——主梁竖弯阻尼和扭转阻尼；

kh、kθ——主梁等效竖弯刚度和等效扭转刚度；(www.daowen.com)

Fh、Mθ——主梁受到的气动升力和气动力矩；

——主梁的竖向位移、速度和加速度；

——主梁的扭转位移、速度和加速度。

对于不可压缩流体的连续方程和纳维-斯脱克斯方程为［13］

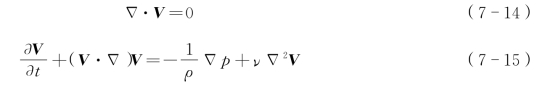
式中 V——流体的速度向量；

ρ——流体密度；

ν——流体运动黏性系数，空气中运动黏性系数常温时取1.5×10-5 m2·s-1。

求解流体方程［式（7-14）、式（7-15）］得到主梁表面的压强，计算主梁受到的升力和力矩；将升力和力矩分别代入主梁振动方程［式（7-12）、式（7-13）］，运用Newmark-β法求解主梁动力响应，将主梁的速度传递给网格，通过动网格技术使主梁运动，然后开始下一个时间步的计算。如此循环进行流固耦合计算得到各时间步的主梁位移。