本节结合《公路桥梁抗风设计规范》（JTG／T 3360-01—2018）将主要的桥梁抗风计算公式做简要介绍。

7.2.1.1 驰振计算

当驰振力系数Cg＜0时，驰振稳定性临界风速可按下式计算［12］：

式中 Ucg——驰振稳定性临界风速（m／s）；

m——构件单位长度质量（kg／m）；

ωb1——结构一阶弯曲圆频率（rad／s），ωb1=2πfb1；

ζs——结构或构件阻尼比；

D——结构断面的特征高度（m）；

Cg——结构断面的驰振力系数，一般可以通过风洞试验或虚拟风洞试验方法获取，参看《公路桥梁抗风设计规范》表7.3.2；

B——构件断面的特征宽度（m）；

——结构断面升力系数的斜率；

CD——结构断面阻力系数。

具有下列特征的结构或构件应进行驰振稳定性检验：①宽高比的钢主梁；②钢桥塔；③断面驰振力系数Cg＜0的钢构件；④受积冰或积雪影响的斜拉索、吊杆（索）及受积冰或积雪影响的钢主梁。

7.2.1.2 颤振计算

常用的平板颤振临界风速Uco计算公式有Van der Put公式、Selberg公式和项海帆公式［12］。

1）Van der Put公式

根据Theodorson平板气动力的精确表达式，由KIöppel等算出无量纲参数的诺模图（其中偏保守地忽略了结构阻尼比），Van der Put将诺模图中的曲线拟合成近似的直线形式，表示为

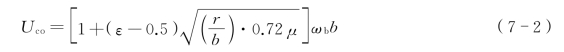
式中 ε——扭弯频率比，

μ——桥面单位长度的质量与空气的密度比，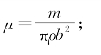

m——桥梁单位长度质量（kg／m）；

b——主梁特征宽度的一半，

r——桥梁的惯性半径（m），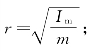

Im——桥梁单位长度质量惯性矩（kg·m2／m）。

2）Selberg公式

根据Theodorson平板气动力公式，Selberg根据Bleich的颤振解得出近似公式：

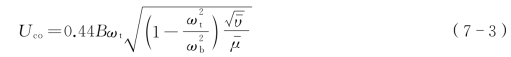
式中 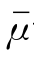——空气与桥面的密度比，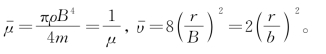

3）项海帆公式

同济大学项海帆教授将KIöppel的诺模图近似地拟合成通过原点的直线，并对斜率做适当调整，得到简化计算公式：

4）桥梁颤振临界风速

式中 ηs——形状修正系数；

ηα——攻角效应系数。

ηs、ηα取值可参看《公路桥梁抗风设计规范》表7.5.4。

7.2.1.3 涡激共振计算

（1）斯托罗哈数。斯托罗哈数将边界层分离及流动的不稳定性这些微观随机特性与表现相对稳定的旋涡脱落频率联系起来：(www.daowen.com)

式中 U——来流速度（m／s）；

D——物体迎风面最大尺寸（m）；

fs——流体绕过物体时旋涡脱落频率（Hz）。

对于指定截面，斯托罗哈数St为一常数。

（2）涡激共振起振风速：

式中 f——结构自振频率（Hz）。

（3）由《公路桥梁抗风设计规范》可知，跨径小于200 m的实腹式桥梁竖向涡激共振振幅可按下式估算［12］：

其中，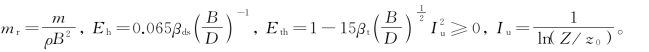

式中 hv——竖向涡激共振振幅（m）；

m——桥梁单位长度质量（kg／m）；

ζs——桥梁结构阻尼比；

βds——形状修正系数；

B——主梁特征宽度（m）；

D——主梁特征高度（m）；

βt——系数，对六边形截面为0，其他截面取1；

Iu——纵向脉动风速设计紊流强度；

Z——桥面的基准高度（m）；

z0——桥址处的地表粗糙高度（m）。

跨径小于200 m的实腹式桥梁扭转涡激共振振幅可按下式估算［12］：

其中，

式中 θt——扭转涡激共振振幅（°）；

Im——桥梁单位长度质量惯性矩（kg·m2／m）；

ζs——结构阻尼比。

（4）《公路桥梁抗风设计规范》规定，当跨径小于200 m时，桥梁在W1风作用及以下风速范围内的涡激共振振幅按下式检验［12］：

竖向涡激共振振幅：

扭转涡激共振振幅：

式中 fv——竖向振动频率（Hz）；

ft——扭转振动频率（Hz）；

γv——涡激共振分项系数。当采用风洞试验获取hv和θt时取1.0，采用式（7-8）计算hv或采用式（7-9）计算θt时取0.8，采用虚拟风洞试验获取hv和θt时取0.8。

低阶模态自振频率较低，对应的涡激共振起振风速低；高阶模态自振频率较高，对应的涡激共振起振风速较高。风速低时可能没有足够的能量来激发涡激共振，所以对于大跨度桥梁还需考虑高阶模态的涡激共振。随着大桥跨径的不断增长，涡激共振已经成为除颤振之外最重要的风致振动问题。规范仅给出了跨径200 m以下的桥梁涡激共振振幅许可值，对于大跨度桥梁涡激共振振幅容许值需要进一步研究。

对于非梁式桥梁，如缆索承重桥梁，在运用7.2.1节公式计算风致振动时，主梁的质量和质量惯性矩要考虑采用等效质量和等效质量惯性矩。其中驰振临界风速计算公式、颤振临界风速计算公式及涡激共振振幅计算公式用于桥梁抗风设计的初步计算。