三角网法绘制等高线的基本步骤包括建立数字高程模型、等高线点位置确定、高程相同等高线点的追踪、等高线光滑输出和高程注记。

1）建立数字高程模型

要直接利用原始离散点建立数字高程模型，必须解决以下几个基本问题：

●地性线、特殊地貌和禁区的处理

●三角网构网的算法

●三角网数字高程模型的点、线、面结构数据信息的存贮结构

（1）地性线、特殊地貌和禁区的处理

测绘等高线时，必须沿山脊、山谷和陡坎边线打点，这些都是重要的地性线。插绘等高线时，要以这些线为基础进行插绘。禁区即等高线不可进入的地物禁区和特殊地貌区域，如江河、湖泊及陡坎、斜坡、陡崖等。在构成三角网数字高程模型时，若只考虑几何条件构网，若不考虑这些线的信息，可能出现三角形与断裂线相交，这必然引起数字高程模型的失真。如在山脊线处可出现三角形穿入地下；在山谷线处可能出现三角形悬空；另外，也可能在某些地方出现三角形的边跨越断裂线的情况。这时，三角网数字高程模型便不能真实地反映实际地形的变化，由其绘制的等高线必然是错误的。

实际构网可以引入控制边与禁区的方法解决这类问题。当某两点存在必然的邻接关系时，则连接这两点而成的边就称为三角网的控制边。如某条地性线上两相邻点连接而成的边，即是控制边。一旦定为控制边，它就控制着整个三角网数字高程模型覆盖地区的地形走向。若给这类地物的边界或特殊地貌禁区在构网时给以特定的标志，那么当等高线追踪到这些边上时就不再往前追踪，这就保证了等高线不会进入这些区域。

（2）三角网构网

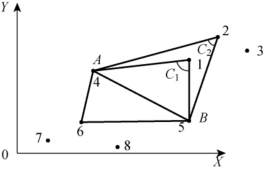
图2-22　三角形构成

三角网构网的基本要求是满足三角网为相互邻接且互不重叠的三角形的集合，每一个三角形的外接圆内不包含其他点。

基于控制边的构网算法，就可以很容易地在构网时引入地性线和地物禁区，且使得程序设计更为简单。其基本思路如下：如图2-22所示，已知某一控制边AB，设其为扩展三角形的基边，现以AB方向左侧点构网为例。为了获得符合实地情况的三角网，可依据余弦定理来判断，C角角值最大者则是要扩展的三角形点。如图2-22，C1的角值大于C2，所以，AB1先构成三角形，这样可以保证由邻近的三点构成三角形，以符合实地形状。确定第一个三角形后，再以这个新三角形的两边为基边向外扩展三角形，直至完成构网。

所以，这种基于边的构网算法可以分为三大步：

第一步，将构网区内的所有控制边相连，形成禁区和地性线；

第二步，以所有控制边为基边向外扩展三角形；

第三步，依次以已形成的三角形的边作为基边向外扩展三角形，直到所有的三角形都不能向外扩展为止。

（3）三角网数字高程模型的点、线、面存贮结构

三角网构成的过程中，同时要解决三角网构网数据信息的存储问题，以便于后面等高线位置确定与追踪。这主要涉及碎部点（三角形顶点）、三角形边和三角形编号等信息，较好的解决办法是建立点、线、面存贮结构的三个表（文件），分别用来记录组成三角形的顶点号、边号、三角形号与邻接关系，其记录格式可为表2-1所示。

表2-1

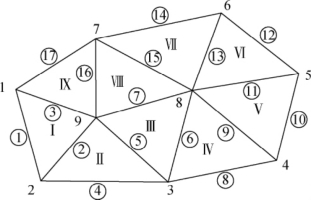
图2-23　点、线、面数据结构

通过索引指针在三个表之间建立相互联系，实现点、线、面之间的互访。图2-23构成的三角形网，其相应的三角形、边的存贮结构分别如表2-2和表2-3所示。由某一个三角形（面），可以检索出构成该三角形的三条边（线），从而又可检索出该三角形的三个顶点（点）。另外，由某条边，又可以很方便地检索出共用该边的两个三角形。这种关系结构，在追踪等高线时是非常有用的。

表2-2　三角形构成信息

2）等高线自动绘制

等高线自动绘制的主要内容包括三角形边上某一高程的等值点平面位置的确定、等值点的追踪和等高线的输出、高程注记等。

表2-3　三角形边、点构成信息

（1）三角形边上等值点平面位置的确定

在三角网构网完成后，需要确定某一高程的等高线是否通过某一边，然后确定其通过的位置（X，Y）。

图2-24　等值点平面位置的确定

设某边上有高程值为HM的等高线通过，那么只有当HM介于该边的两个端点高程值之间时，等高线才通过该三角形边，如图2-24所示，则其判别条件为：(www.daowen.com)

当ΔH＜0时，则该三角形边上有该等高线通过；否则，说明该边上没有该等高线通过。式中H1和H2分别为三角形该边上的两个端点的高程。

当判别式ΔH=0时，说明等高线正好通过三角形边的端点（起点或终点），为了便于处理，在精度允许范围内将端点的高程值加上一个微小值（如0.000 1m），使其值不等于HM。

当确定了某条边上有等高线通过后，即可由下式来求取该边上等值点的平面位置：

式中，（XZ1，YZ1，H1）和（XZ2，YZ2，H2）分别为三角形边两端点的三维坐标，（XM，YM，HM）为等值点的三维坐标。

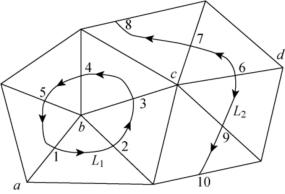
图2-25　等值点追踪

（2）等值点的追踪和等高线输出

确定等值点的平面位置后，就可以对相同高程点进行等值点的追踪。一般有两种情况：一种是闭曲线，如图2-25中的L1所示；另一种是开曲线，如图2-25中的L2所示。

等值点的追踪思路为：首先确定本区域中高程的取值范围（最大与最小高程），根据选定的等高距h，确定起始追踪高程，如设定当前追踪的等高线高程Hi。从三角网数字高程模型的第一条边开始顺序扫描，判断扫描边上是否有该高程值的等高线通过，若有，则将该边作为起边追踪。

如果是闭曲线其追踪过程如图2-25所示，扫描过程中发现边ab上有等高线通过，则将其作为起边并追踪出1号等值点，依次向下追踪出2、3、4、5号等值点后，又追回到边ab上，这即为一闭曲线追踪完毕。

若为开曲线，其追踪过程如图2-25所示，扫描过程中发现cd边上有等高线通过，则将其作为起边并追踪出6号等值点，依次向下追踪出7、8点而到达边界，这说明当前追踪的为一开曲线，再回到起边cd向相反的方向追踪出9、10号点又到达边界，则整条开曲线追踪完成。这时还需要对后半链追踪出的点进行逆排序，即按10、9、6、7、8的顺序排列后半链等值点，从而合并而成为一条完整的开曲线。

对追踪出的等值点坐标，可按一定的数据结构组织存放，以便于后续的等高线光滑与输出。

等高线追踪完成后，即可进行绘制与光滑输出。

光滑处理的基本原理是曲线拟合，选择不同的拟合算法，将得到不同的平滑结果。为了适应不同的地形，平滑处理程序可以包含不同的拟合算法，以得到最接近实际的结果。常用的曲线拟合方法有线性迭代法（抹角法），分段三次多项式拟合、二次多项式加权平均法和张力样条插值法等。

3）高程的注记

高程的自动注记内容包括离散点的注记和计曲线的注记。

（1）离散点的注记

对离散点的注记，一般有自动与手工两种方法：

自动选取注记点的基本思想是将整个绘图区按照注记的密度要求分成若干个相等的方格，每一方格中只能选取一个注记点，这个注记点要尽量接近方格的中心面又不至于注记字符压盖地物。采用这种方法，能够保证注记比较均匀，但是不能保证注记点具有代表性，有可能漏掉某种特征点的注记（如山顶点、谷底点等）。

手工注记时输入具有代表性的特征点的点号，根据给定点号来注记高程数字。在实际处理中，可以采用两种相结合的方法，对于那些必须要注记的特征点，首先输入其点号，以保证优先注记这些点，对普通地物点则采用第一种方法，均匀自动选取注记位置。

（2）计曲线的自动注记

按照图式规范要求，计曲线要加粗并注记出它的高程值，而且要保证注记的字头朝向高处。完成计曲线的自动注记步骤如下：

①计曲线的判断

如果要求每隔4根进行加粗注记，那么对计曲线的判断可按下式进行的：

其中，ΔH为等高距，［　］为取整符号。若Δ=0，则高程值为H的等高线即为计曲线。

例如，当ΔH=1，H=15时，代入（2-35）得：Δ=0，所以该曲线为应加粗并注记高程的计曲线。

②注记位置的确定

图2-26　高低面判断

对于加粗等高线上合适注记位置的寻找，是基于当等高线上某一段曲线的曲率较小，而长度又能满足写字要求时则认为在一段曲线适合注记。

③注记字头朝向高处

为了满足注记字头朝向高处，就要知道等高线前进方向的高低面。如图2-26所示，在△P1P2P3中，等高线的追踪顺序是由P1P2边到P1P3边，则等高线的走向是由1→2，通过比较P1、P2、P2点的高程值就可以确定出等高线前进方向的高低面。