面状符号具有实际的二维特征，它以面定位。其定位线一般是一个封闭的区域。大比例尺图式规定，土质和植被符号一般按照整列式、散列式和相应式三种方法配置面积符号。面状符号自动绘制就是在一定轮廓区域内用填绘晕线或沿晕线上配置一系列的点状符号来表示。所以，在轮廓区域内填绘点状符号，其实质是首先用绘晕线的方法计算出点状符号的中心位置，然后再绘制点状符号。下面首先介绍在多边形轮廓线内绘制晕线的方法，然后讨论一般面状符号的自动绘制问题。

1）多边形轮廓线内绘制晕线

如图2-17所示，多边形轮廓线内绘制晕线应有的参数为：轮廓点坐标（xi，yi）（i=1，2，…，N）、轮廓点个数N、晕线间隔D以及晕线和x轴夹角α。轮廓线内绘制晕线可按如下步骤进行：

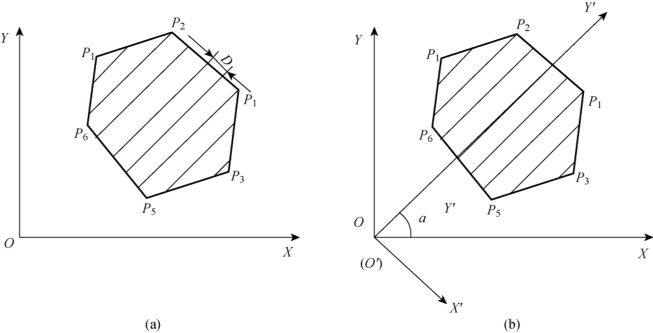
图2-17　轮廓线内绘制晕线

（1）对轮廓点坐标进行旋转变换

为了处理简单起见，将原坐标系XOY顺时针旋转一个角度（90°-α），使得新坐标系x′o′y′的y′轴和晕线平行，其中α为晕线和x轴的夹角，各轮廓点在变换后新坐标系中的坐标，可按以下公式计算：

式中，（xi，yi）为轮廓点在原坐标系XOY中的坐标，（x′i，y′i）为相应点在变换到新坐标系x′o′y′中的坐标。

（2）求晕线条数

在新坐标系中找出轮廓点x′方向的最大坐标x′max和最小坐标x′min，则可求得晕线条数M为：

当时，晕线条数应为M-1。把整个轮廓区域内的晕线按从左到右的次序从小到大顺序进行编号，第一条晕线编号为1，最后一条晕线编号为晕线条数M。

（3）求晕线和轮廓边的交点

在变换后的新坐标系中，对编号为j的晕线，则

式中，j=1，2，…，M。对于第j条晕线是否通过轮廓线的第i条边，可以简单地用该条边两端点的x′坐标来判别，即当（x′i-x′j）·（x′i+1-x′j）≤0成立，就说明第j条晕线与第i条轮廓边有交点。晕线和轮廓边的交点可按下式计算：

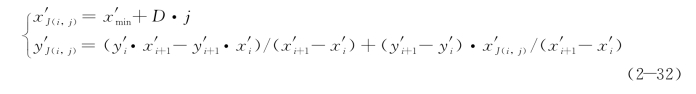(www.daowen.com)

式中，x′J（i，j）和y′J（i，j）为第j条晕线和第i条轮廓边的交点坐标，（x′i，y′i）和（x′i+1，y′i+1）为第i条轮廓边的端点坐标。

一般来说，每条晕线与轮廓边的交点总是成对出现的。但是当晕线正好通过某一轮廓点时，就会在该点处计算出两个相同的点，这有可能引起交点匹配失误。为了避免这种情况出现，在保证精度的情况下，将轮廓点的x′i加上一个微小量（0.01），即当x′i=x′j时，令x′i=x′i+0.01。

（4）交点排序和配对

在逐边计算出晕线和轮廓边的交点后，需对同一条晕线上的交点按y′值从小到大排序，排序后两两配对，以便确定每条晕线的起点和终点。

（5）晕线输出

交点排序和配对完成后，即可进行晕线输出。在输出晕线之前，需要把晕线交点坐标先变换到原坐标系XOY中。

2）面状符号的绘制

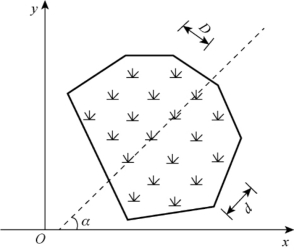
图2-18　面状符号绘制

面状符号绘制时，其绘图参数有：轮廓边界点个数N，轮廓边界点坐标（xi，yi）（i=1，2，…，N），符号轴线间的间隔D以及轴线和X轴的夹角α，每一排轴线上符号的间隔d，如图2-18所示。

面状符号的自动绘制步骤描述如下：

（1）确定符号注记轴线

按照符号列轴线间的间隔D以及轴线和X轴的夹角α计算出面状符号的轴线。

（2）计算面状符号的中心位置

计算轴线（即晕线）长度，根据轴线长度和轴线上符号的间隔d，按均匀分布的原则计算注记符号的中心位置。

（3）填绘面状符号

根据面状符号代码，在符号库中读取表示该符号的图形数据，在相应的符号中心位置上绘制面状符号。