1）基本线型绘制

在地图中经常要用各种线状符号来表示各种不同的地物。按其符号的复杂程度来分，可分为简单线状符号和复杂线状符号，但都是由一些基本线型的直线、曲线等部分组成。地图上用到的线型尽管很复杂，但归结起来主要有以下几种（图2-12）：

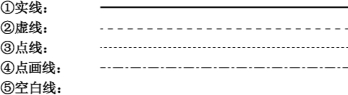
图2-12　基本线型

这些基本线型可以用以下绘图参数来表示：定位点个数N和定位点坐标（xi，yi）（i=1，2，…，N），实步长D1，虚步长D2和点步长D3。通过给定不同的步长值，即可设置不同的线型。例如当D2=D3=0时，即为实线；当点步长D3=0时，即为虚线；当D1=D2=0时，即为点线。

对于虚线，其绘制方法是：即D3=0，如图2-13所示，根据给定的步长D1和D2，沿着定位线的路径和方向，分别计算其对应的两个端点坐标，然后连接实步长部分即可。

2）平行线绘制

平行线是由两条间距相等的直线段构成。很多线状地物符号都是由平行线作为基本边界，再加绘一定的内容而构成，如铁路、依比例围墙等，因而平行线是绘制很多线状地物符号的基础。

平行线的绘图参数为：定位线（母线）节点个数和定位节点坐标（xi，yi）（i=1，2，…，N），平行线宽度w，平行线的绘制方向，即在定位直线的左方还是右方绘制。如图2-14所示，假定在定位线左方绘制平行线，定位线的节点坐标为（xi，yi），对应平行线的节点坐标设为（x′i，y′i）。

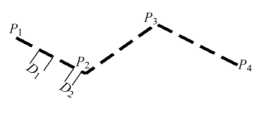
图2-13　虚线绘制

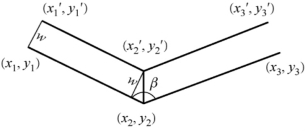
图2-14　平行线绘制

其平行线的节点坐标可按下式计算：(www.daowen.com)

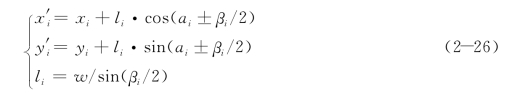
式中，ai为第i条线段的倾角，βi为第i个节点的左夹角，ai的计算公式为：

这里需要注意的是，当i=1和i=N时，要令β值为π，即β1=βn=π，且当i=N时，要令an=an-1。

3）复杂线状符号的绘制

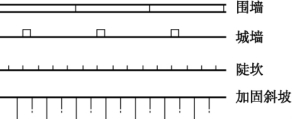
图2-15　线状符号

复杂的线状符号除了在每两个离散点之间有趋势性的直线、曲线等符号以外，有些线状符号中间还配置有其他的符号。如图2-15所示，围墙符号是平行线为基准，中间配以等分的间隔线；陡坎符号，除了定位中心线以外，还配置有短齿线，加固陡坎，中间再加短线和圆点；城墙符号是以基准线为依托，等间隔配置小矩形构成。对于这些沿中心轴线按一定规律进行配置的线状符号，可以用比较简单的数学表达式来描述。以陡坎符号为例，设D1为相邻两齿间的距离，D2为齿长，基准线的各点坐标为（xi，yi）（i=1，2，…，N），参照图2-16，描述该符号基本轮廓的一组公式为：

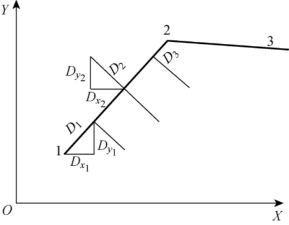
图2-16　线状符号计算

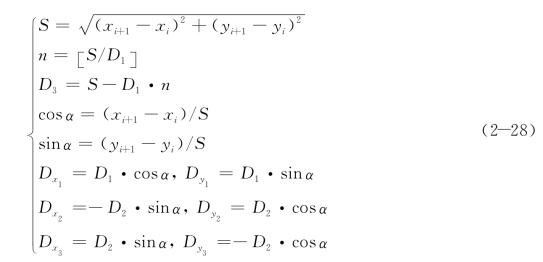
式中，［　］表示取整符号，S为两离散点之间的距离，n表示两离散点间的齿数，D3为两离散点间不足一个齿距的剩余值，（Dx1，Dy1）为第一点齿心的相对坐标，（Dx2，Dy2）、（Dx3，Dy3）为齿端对齿心的相对坐标，以后各点，依此类推。

当计算出齿心和齿端坐标以后，根据不同的线状符号特点，采用不同的连接方式就可产生围墙、铁路、城墙等线状符号。