目前多边形裁剪的常用方法有逐边裁剪算法和边界裁剪算法。

边界裁剪算法思路是以窗口的有效边界段和处于窗口内的多边形部分组成新的裁剪后的多边形。逐边裁剪算法思路是把整个多边形先相对于窗口的第一条边界裁剪，然后再把形成的新多边形相对于窗口的第二条边界裁剪，如此进行到窗口的最后一条边界，从而把多边形相对于窗口的全部边界进行裁剪。

设有多边形和裁剪窗口的相对位置如图2-10所示，逐边裁剪算法的步骤为：

（1）取多边形顶点Pi（i=1，2，…，n），将其相对于窗口的第一条边界（有边界）进行判别，若点Pi位于边界的靠窗口一侧（可见侧），则把Pi记录到要输出的多边形顶点中，否则不记录。

如图2-10（a）中P1、P4点，不记录到要输出的多边形中。

（2）求多边形与窗口有边界的交点(www.daowen.com)

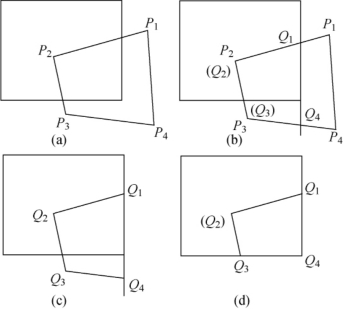
图2-10　多边形的裁剪

因为P1、P2位于窗口右边界的异侧，因此要求出该条边与窗口右边界的交点，记为Q1作为新多边形的第一个顶点，同时把P2、P3作为新多边形的第二、第三个顶点，记为Q2和Q3。P3、P4也是位于窗口右边界的异侧，也要求交点，记为新多边形的另一顶点Q4，这样就得到了新多边形Q1 Q2 Q3 Q4，如图2-10（b）所示。

（3）新多边形相对于窗口其他边裁剪

得到新的多边形后，用新的多边形重复上述步骤（1）、（2），依次对窗口的下边界、左边界、上边界进行判别裁剪，不断获得新的图形，直至最后完成所有裁剪，获得裁剪的最后结果，如图2-10（c）、2-10（d）所示。