在地形图绘制过程中遇到的曲线归纳起来有两大类：一类是规则曲线，如圆、椭圆、三角函数曲线等，他们可以用一个规则的方程式来描述。另一类为不规则曲线，如地形图上的等高线、道路、水系等曲线符号，常规测图方法中由手工来绘制这类曲线，而应用计算机绘制这类曲线必须采用一定的数学方法（曲线拟合法）来完成，即用一些测量的离散数据用拟合光滑方法来生成曲线。

曲线拟合包括插值与逼近两种基本方法，插值要求曲线通过所有给定点（型值点），逼近则不要求曲线通过所有给定点（型值点），只要求反映曲线整体的变化趋势。因此，在要求较高时，应采用插值拟合曲线绘制方法。

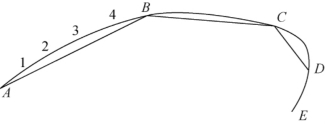
图2-7　加密点的曲线光滑

如图2-7所示，A、B、C、D、E是5个数据点，在AB、BC等线段上用一定的数学方法插进一系列加密点，如1、2、3、4等。对所有的点依次相连得到一连串边长很短的折线，由于相邻两点距离很短，看起来就是一条比较光滑的曲线。因此，曲线光滑就是根据给定的一系列特征点建立曲线函数，计算加密点来完成曲线光滑连接。

曲线光滑的数学方法很多，如最小二乘法、线性迭代法（抹角法）、抛物线加权平均法、分段三次多项式插值法、张力样条函数插值法等。(www.daowen.com)

最小二乘法的实质是拟合点与给定点的偏差为最小。该方法数学上是严密的，但是拟合曲线不一定经过给定点（型值点）。

线性迭代法（抹角法）的实质是反复进行线性迭代产生加密的折线，从而对曲线进行光滑处理。其缺点是光滑后的曲线会偏离原始数据点，有较大的位置误差，精度低。

抛物线加权平均法曲线光滑是根据给定的曲线特征点顺序每相邻的三个点构成一条抛物线，相邻两点间的前后抛物线的重合部分用加权平均方法光滑曲线。该方法数学上是严密的，计算过程简单，能保证光滑曲线通过给定点，但需要在首末处插补点，并且分段较多。

分段三次多项式插值法是在每条直线段建立一条三次曲线，并且整条曲线上有连续的一阶导数。该方法数学上是严密的，拟合曲线通过给定点，但计算过程复杂，在曲线变化较大时，会出现相邻曲线相交的现象；另外，由于导数的计算需要5个点，所以，在首末处插补点两点。

张力样条函数插值法是在一般的三次样条函数中引入一个张力系数σ，当σ→0时，张力样条函数就等同于三次样条函数；当σ→∞时，张力样条函数就退化为分段线性函数，即相邻节点之间以直线连接。可以选择适当的张力系数σ，以改变曲线的松紧度，使曲线的走向更加合理。张力样条函数插值法可以克服其他曲线拟合方法的不通过给定点和拟合曲线相交的现象，是地形图绘制时曲线绘制的一种常用方法。