1．单元的选取及网格划分

有限元分析模型中节点单元的选取是十分关键的问题，直接关系到分析结果的正确与否。在管节点的有限元分析中，有限元模型单元大多数采用弹塑性壳单元，虽然实体单元计算精度更高，但是耗时。根据第2章2．2．5节中的分析，在本次数值模拟中选取三维四节点弹塑性壳单元Shell181作为分析单元。

按所选取的单元，对K型搭接节点试件按隐藏焊缝焊接与否分别建立有限元模型，其截面尺寸与试验试件完全相同（表5-1）。有限元建模时钢材的本构关系采用多线性随动强化模型、Von-Mises屈服准则，考虑了材料非线性和几何非线性，往复加载时考虑Bauschinger效应。根据材性试验得到的弹性模量、屈服强度、泊松比等来定义模型的单元特性。图5-19为节点试件的有限元模型，模型的节点数为3735，单元数为3482。在焊缝区域进行了网格加密。

2．焊缝的模拟

连接焊缝的模拟采用第4章4．2．4的方法进行模拟。

3．边界条件及加载方式

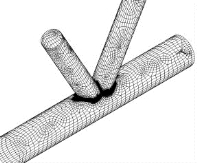
图5—19　节点试件有限元模型

(www.daowen.com)

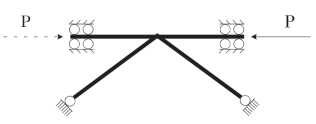
图5—20　边界条件和加载方式

对于节点在低周往复荷载作用下的滞回性能研究，为了全面考察钢管相贯节点弹塑性分析的全过程，结合钢管模型试验的加载特点，设定了图5-20所示的加载模式，即：支管端部铰接，并限制节点平面外位移，在主管两端加载，实现节点滞回模拟。

加载方式采用在弦杆端部加载点施加一定大小的集中力P。当结构进入塑性以后，其变形与加载路径和加载历史有关。为了模拟实际的加载历史，在有限元分析中，采用变幅加载模式，即在每级荷载下按静力荷载试验的模式分级加载和卸载，再反向加卸载，进行低周循环，每级加载的增量荷载为50k N，加载路径同试验加载。

4．求解器的选择

计算模型的求解采用Newton-Raphson进行非线性迭代求解。非线性求解采用2范数收敛准则，即：

式中：｛R｝——不平衡力向量；

Rref——收敛容许误差，同时有