滞回性能试验结果通常用荷载-变形的滞回曲线及有关参数来加以分析。从国内外的研究情况来看，节点的抗震性能应从破坏形态、强度、延性和耗能能力几方面进行综合评定和对比，以判断节点是否具有良好的恢复力特性，即是否具有足够的承载能力，一定的变形能力，及较好的耗能能力［5］。

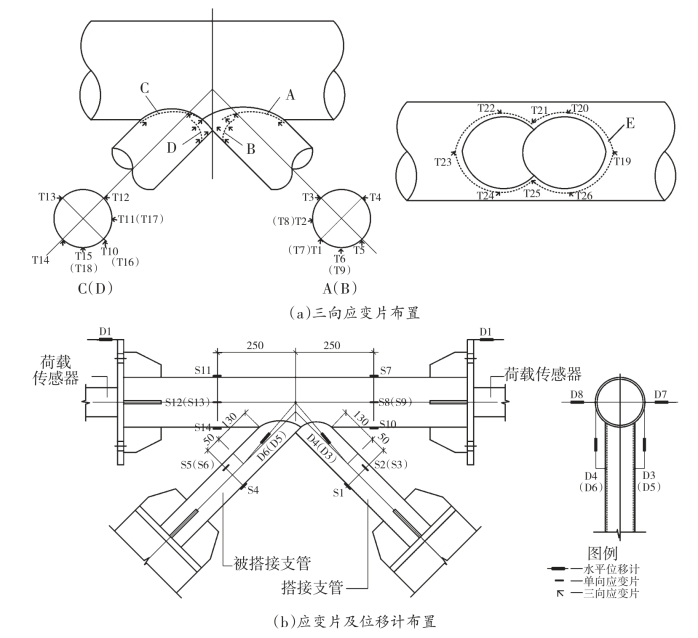
图5—5　测点布置

1．节点破坏特征

主管端轴向加载模式比较符合实际结构中的管桁结构受力情况。在反复荷载作用下，K形搭接节点因主管刚度大于支管刚度以及K型节点的空间效应的影响，在荷载达到极限荷载前，节点的整体变形比较小，但支管一旦达到屈服，节点整体变形迅速增大。

试件主要的破坏形式为：试件K-YH01当搭接支管受拉时，搭接支管与被搭接管、主管之间的连接焊缝发生断裂；试件K-YN01为搭接支管根部发生局部屈曲，但不是很明显；试件K-YH02为搭接支管与被搭接管、主管之间的连接焊缝发生微小裂纹，搭接支管根部发生“马足式”屈曲；试件K-YN02为搭接支管与被搭接管、主管之间的连接焊缝发生裂缝，搭接支管根部发生“马足式”屈曲。

可以看出，无论是隐藏焊缝焊接的节点还是隐藏焊缝不焊接的节点，破坏的位置均发生在搭接支管上。当搭接支管受拉时，搭接支管与被搭接支管、主管的连接焊缝发生裂缝或断裂；当搭接支管受压时，搭接支管的端部发生“马足式”屈曲。图5-6为各试件的破坏形态。

图5—6　试件破坏模式

总之，节点主要破坏现象有：①搭接支管与被搭接管、主管之间的连接焊缝断裂；②搭接支管与被搭接管、主管之间的连接焊缝出现裂缝；③搭接支管根部“马足式”屈曲。

2．支管端部荷载-位移滞回曲线

图5-7给出了各试件的荷载-位移滞回曲线，纵坐标为主管端轴向荷载P，被搭接支管受拉为正，受压为负；横坐标为支管相对于主管的变形Δ，正负号与荷载方向相同。通过比较4个节点试件的滞回曲线可以看出：①各个试件的滞回曲线基本呈梭形，在主管轴向荷载低于200k N时，各节点的变形基本是一致的。②在相同荷载下，K-YN01和K-YN02的变形大约是K-YH01和K-YH02的变形的1．2倍。这说明隐藏焊缝不焊接节点的塑性变形能力强，具有很好的地震能量吸收能力和优越的抗震性能。③K-YH02（YN02）的滞回曲线略显反“S”型，这说明随着β值的增大，节点刚度降低，出现了明显的滞回曲线反“S”型。

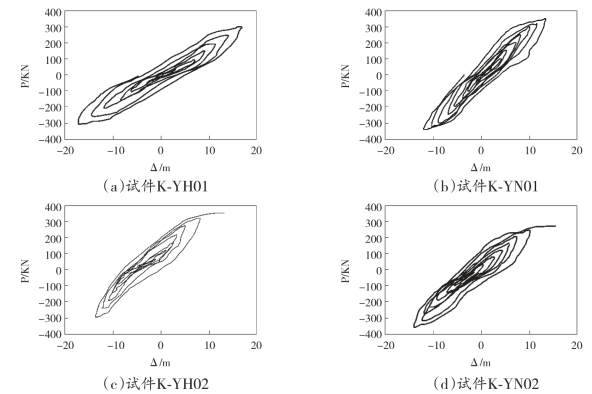
图5—7　试件滞回曲线

3．骨架曲线

图5-8给出了两种不同焊接方式下试件的骨架曲线。可以看出，隐藏焊缝焊接与否对承载力的影响变化不是十分显著，骨架曲线的形状基本一致，隐藏焊缝焊接节点的承载力稍大于隐藏焊缝不焊接的节点。

以达到屈服荷载Py时的变形进行分析：正向加载（左→右）被搭接管受拉，搭接管受压，隐藏焊缝不焊接节点的变形是隐藏焊缝焊接节点变形的1．2倍。随着β值的增加，内隐藏焊缝不焊接节点的变形降低了约6%，内影藏焊缝焊接节点的变形降低了11%。反向加载（右→左）被搭接管受压，搭接管受拉，隐藏焊缝不焊接节点的变形是隐藏焊缝焊接节点变形的1．1倍。随着β值的增加，内隐藏焊缝不焊接节点的变形降低了约10%，内影藏焊缝焊接节点的变形降低了18%。节点内隐藏焊缝的焊接降低了节点的延性，对节点的抗震不利。

4．节点应变分布规律

布置在支管根部及主次管相贯面周围的三向应变花有26片，为了解该部位的应变强度变化与分布规律，对应变测点的数据进行了分析，以探究钢管搭接节点在反复轴向荷载作用下的破坏机理。图5-9、图5-10为弦杆及腹杆上三向应变片在不同角度方向的布置。L-R（R-L）为弦杆端自左-右（右-左）进行加载。

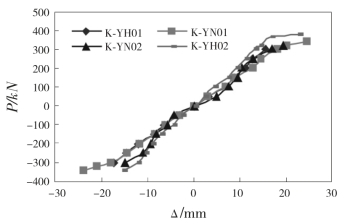
图5—8　P-骨架曲线

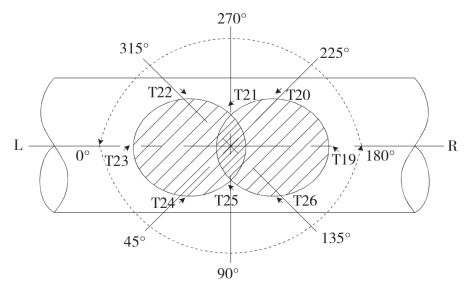
图5—9　弦杆上应变片布置示意

取K节点弦杆端L-R（R-L）加载300KN荷载步，对节点域弦杆及腹杆上的应变分布规律进行研究。主要探讨隐藏焊缝焊与不焊两种情况下节点域的应变分布规律。

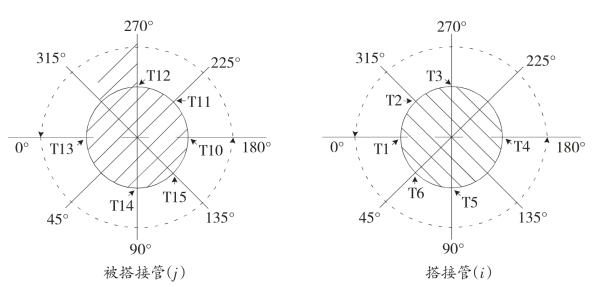
图5—10　腹杆上应变片布置示意

（1）节点域弦杆上的应变分布规律

图5-11给出了不同节点试件弦杆相贯线周边测点应变强度分布规律。依据图5-9，纵坐标为测点最大应变，横坐标α为测点在弦杆上的水平投影与水平线之间的夹角。

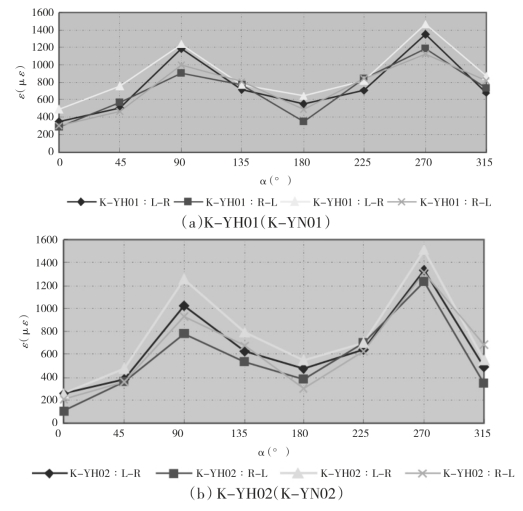
图5—11　弦杆上测点的应变分布

从图中可以看出，弦杆自左→右（L-R）加载至300KN时，节点的变形大于R-L方向加载。节点的最大变形发生在鞍点处，由于节点的空间效应影响，冠点处的变形最小。对于沿弦杆轴线方向两侧变形不一致，可能是在加载当中，加载点存在初偏心所致。K-YH02、K-YH01的变形小于K-YN02、K-YN01的变形，即隐藏焊缝焊接节点的变形小，也就是说，隐藏焊缝焊接降低了节点的柔度。本次试验的节点试件，主支管管径比都小于0．5，隐藏焊缝焊接节点变形降低得不是十分明显，同时，K-YH02（K-YN02）试件的节点变形小于K-YH01（K-YN01）的变形。

（2）节点域腹杆上的应变分布规律

图5-12给出了不同节点试件腹杆相贯线周边测点应变强度分布规律。依据图5-9，纵坐标为测点最大应变，横坐标α为测点在弦杆上的水平投影与水平线之间的夹角。

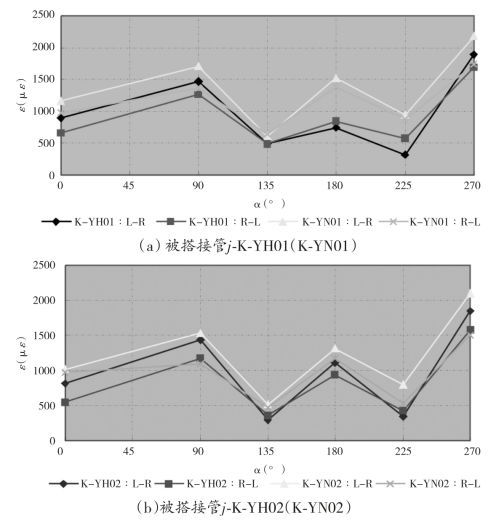
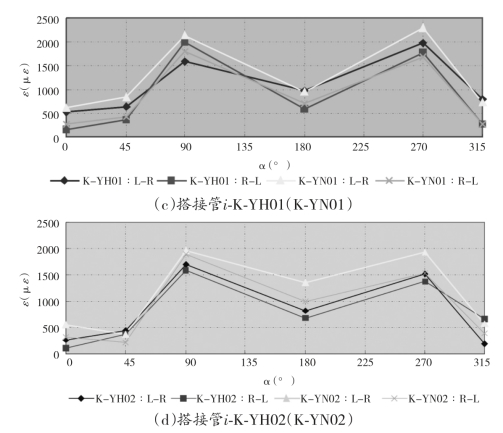
图5—12　腹杆上测点的应变分布

从图中可以看出，总体上腹杆测点的变形大于弦杆测点变形，隐藏焊缝不焊接的节点变形大于隐藏焊缝焊接节点的变形。在弦杆加载模式下，搭接管的变形大于被搭接管的变形。K-YH02（K-YN02）试件的节点变形小于K-YH01（K-YN01）的变形，这说明主支管管径越接近，节点的变形会越小。

5．节点承载力分析

本书1．2．2表1-4给出了圆钢管K节点的各种破坏模式。其中弦杆管壁屈服、弦杆管壁冲剪破坏、主支管连接焊缝破坏是最普遍的三种破坏模式。因此，在对钢管结构K节点承载力评价方面，主要计算四部分内容：①失效模式-弦杆管壁屈服对应的K节点承载力；②失效模式-弦杆管壁冲剪破坏对应的K节点承载力；③K节点连接焊缝的承载力；④腹杆杆件的承载力。现对各部分的计算如下：

（1）弦杆管壁屈服模式对应的K节点轴向极限承载力

我国钢结构设计标准GB50017-2017［10］，对K型圆管相贯节点在支管轴心受压和受拉时，在管节点处的承载力按下式计算：

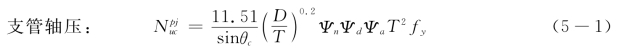
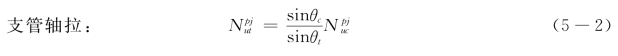
式中：θc（θt）——受压（拉）支管轴线与主管轴线之夹角

Ψn，Ψd，Ψa——参数，分别按下列各式计算：

，当节点两侧或一侧主管受拉时，取Ψn＝1 Ψd＝0．069＋0．93β（β≤0．7）或Ψd＝2β-0．68（β＞0．7）

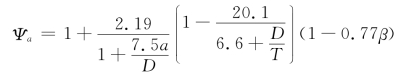
σ为节点两侧主管轴心压应力的较小绝对值

α为两支管间的间隙，对于搭接管，取α＝0

（2）弦杆管壁冲剪破坏模式对应的节点轴向极限承载力

图5-13是CIDECT技术文件［3］采用的冲剪模型，其破坏模式是由于垂直于弦杆的荷载分量N1·sinθ1引起的。节点的强度为有效冲剪面积乘以有效冲剪抗力．因此，对于K节点冲剪失效的极限承载力为：

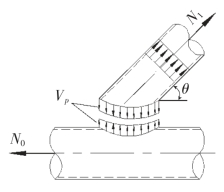
图5—13　K节点冲剪模型

（3）K节点连接焊缝轴向承载力

GB50017-2017规定，在管结构中，支、主管的连接焊缝可视为全周角焊缝，角焊缝的计算厚度沿支管周长是变化的，当支管轴心受力时，平均计算厚度可取0．7hf。圆钢管相贯线焊缝的计算长度按下列公式计算：

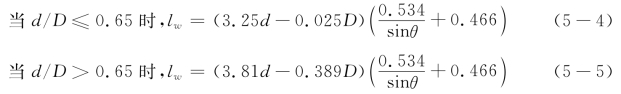
K节点连接焊缝的轴向承载力为：

在计算当中，焊缝材性取与钢管材性一致，因此

（4）支管轴向承载力

支管与主管连接节点的根部截面的全截面屈服轴力为：

(www.daowen.com)

表5-3为各节点在往复加载到节点破坏时的试验实测承载力Nu与按照上述公式计算得到的各试件承载力的计算结果。在计算当中，规范强度设计值均已置换为钢材屈服值。表中的Ny为根据Kurobane［34］准则确定的节点轴向屈服承载力。

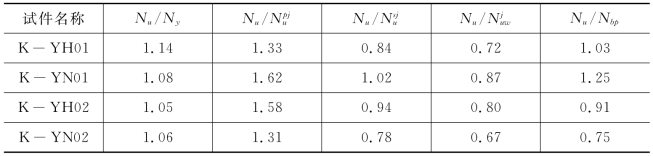
表5-4中分别对各试件进行了承载力比较。Nu／Ny可以定义管桁结构的节点承载力储备，表示节点开始屈服后承载能力继续增长的能力。

从表中可以看出，支、主管直径比β值越小，试件的承载力储备越大。试验实测的节点承载力均高于对应主管管壁屈服破坏模式的承载力公式计算值，均小于对应主管冲剪破坏模式的承载力公式计算值，跟支管轴向承载力比较接近。因此可以认为主管管壁塑性屈服破坏模式起控制作用，而支管轴向承载力引起的节点破坏也不容忽视。

表5-3　节点轴向承载力计算（k N）

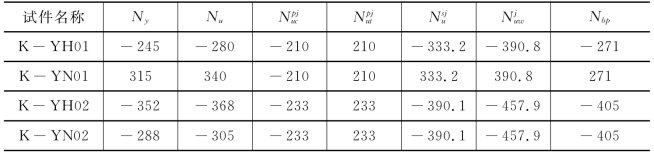
注：＋表示正向加载；-表示反向加载。

表5-4　节点轴向承载力比较

6．节点刚度退化分析

根据《建筑抗震试验规程》（JGJ101-2015）［27］的规定，试件的刚度可用割线刚度来表示，割线刚度可按图3-18定义并应按下式计算：

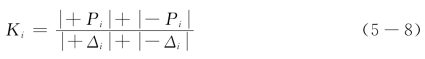
其中，Ki—第i次峰点的割线刚度；

Δi为第i次峰点的位移值；

Pi为第i次峰点的荷载值。

按上式计算各个试件的割线刚度随位移的变化规律如图5-15所示，相应于Ki时的位移取为

从图5-15可以看出：

（1）隐藏焊缝焊与不焊对节点刚度的影响不是十分明显。隐藏焊缝不焊接的刚度稍低于隐藏焊缝焊接的节点。

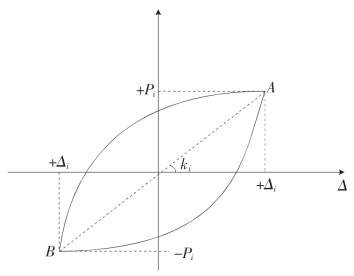
图5—14　Ki的定义

图5—15　Ki-Δi关系曲线

（2）在位移较小节点还未屈服时，随着β、τ值的增大，节点的刚度也在增大；节点发生屈服后，随着位移的增大，节点刚度开始逐渐退化，但试件割线刚度退化缓慢，说明搭接节点的空间效应及搭接焊接对节点的刚度影响明显。

7．节点变形能力分析

一般用节点延性比μ来衡量节点的变形能力。该指标是节点抵抗地震作用能力的有效度量，延性比越大，节点域进入塑性后承受大变形的潜能越大，强震时耗能能力越强，节点延性越好。

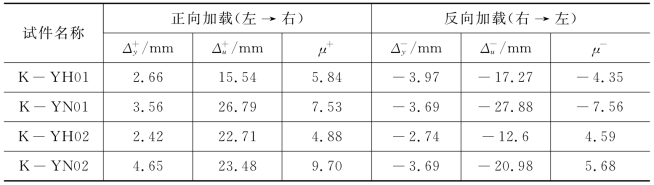
管节点的延性比μ＝Δu／Δy。Δu为骨架曲线上最高点所对应荷载的位移，Δy为试验中荷载变形曲线第一次出现明显弯曲所对应的位移［34］。表5-5给出了节点正向加载及反向加载的屈服位移、极限位移及延性系数。从表中对比可以发现，所有试件的延性系数都比较高，隐藏焊缝焊接的节点的屈服位移及极限位移小于不焊接的节点。隐藏焊缝不焊接节点的抗震性能越更好。

表5-5　试件的屈服位移、极限位移及延性系数

8．节点耗能分析

根据日本学者秋山宏的基于能量的抗震设计原理［80］，结构在地震作用下体系的地震响应可以表示为如下形式：

式中，We为弹性振动能量；

Wp为累计塑性变形能；

Wh为阻尼消耗能量；

Eeq为地震动输入结构的总能量。

钢管节点滞回曲线包络图所包容的面积即为Wp的度量。除了利用滞回曲线包络图面积衡量节点试件的耗能能力外，能量耗散系数和累计能量耗散比也是常用的衡量指标。

（1）能量耗散系数

结构及构件的能量耗散能力的数值反映，通常用能量耗散系数来表示。利用值的大小来量化评价节点的耗能能力。根据《建筑抗震试验规程》（JGJ101-2015）的规定，试体的能量耗散系数E应按下式来计算：

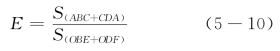
其中，S（ABC＋CDA）——滞回环ABC和滞回环CDA的面积之和；

S（OBE＋ODF）——三角形OBE和三角形ODF的面积之和。

各参数的几何意义如图5-16所示：

根据图5-7的滞回曲线绘制的主管荷载-位移变形曲线的包络图如图5-17所示。

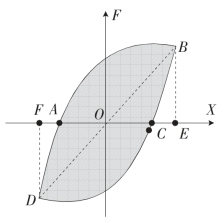
图5—16　滞回曲线包络图与能量耗散系数计算

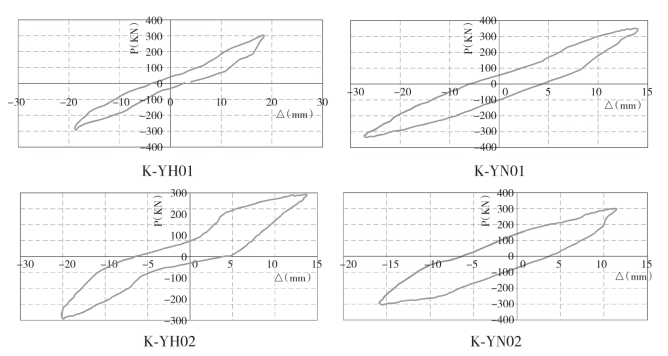
图5—17　节点试件滞回曲线包络

表5-6为各试件的能量耗散系数的计算值，由于K-YH01在试验当中，焊缝破坏提前卸载，K-YN01没有破坏，这组试件对钢管节点的能量耗散的表现不是很准确。总体来看，对于支主管直径比比较小的钢管搭接节点，耗能能力不是很明显，隐藏焊缝不焊接的节点略好于焊接的节点。这可能与主管端加载有一定的关系，对以后管节点加载试验的方案优化具有指导作用。

表5-6　节点轴向滞回曲线包络图面积和能量耗散系数

图5-18为能量耗散系数E随相对位移变化的曲线。可以看出，在相同位移下，隐藏焊缝不焊接的节点耗能能力大于隐藏焊缝焊接的节点。随着β、τ、Ov的增大，节点的耗能能力也在增大。

（2）累积能量耗散比ηα

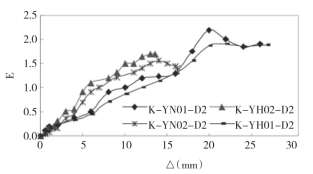
图5—18　能量耗散系数-位移关系曲线

衡量节点耗能能力的另一重要指标为累计能量耗散比，其定义为：

式中：——第i循环正向荷载位移曲线的面积；

——第i循环负向荷载位移曲线的面积；

Sy——首次屈服的耗能面积，Sy＝（1／2）pyΔy，Py、Δy分别为屈服荷载和屈服位移。

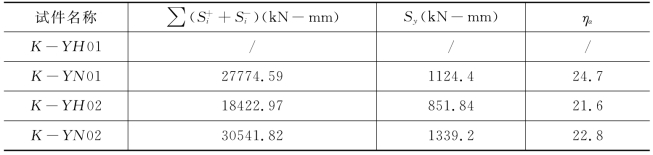
表5-7给出了各试件滞回曲线的累积能量耗散比。从表中可以看出，隐藏焊缝不焊接节点的耗能好于隐藏焊缝焊接的节点。

表5-7　节点轴向滞回曲线累积能量耗散比