在损伤累积演变方程的基础上，进一步研究焊材在循环荷载作用下的本构关系，建立其损伤累滞回模型。参考文献［63-67］，具体包括：首次加载曲线，即低周疲劳试验时起振前的单调拉伸曲线，可由单向拉伸试验拟合获得；骨架曲线，即不同应变幅控制加载时得到的应力峰值点连线；滞回曲线模型，包含滞回准则，加载曲线和卸载曲线。

滞回模型需要具备以下特点：①能够体现出损伤累积过程，损伤不可逆的特点，这通过引入损伤变量实现；②体现出刚度退化和等幅循环时应力幅值退化的特点；③具有递推性，可适用于不同应变幅值控制情况。

1．首次加载曲线

首次加载曲线通过单向拉伸试验拟合获得，并考虑损伤的影响。图3-15为焊材的应力-应变试验曲线，屈服阶段后的曲线接近Ramberg-Osgood模型。故在此模型的基础上，进行修正，引入损伤变量来描述焊材受单向拉伸荷载时，在屈服阶段以后的应力-应变关系，结合损伤理论形成损伤本构关系如式（3-22）中ε≥εy2的情况。损伤变量计算公式由“3．2．1”中推导获得，其中损伤体现在将损伤前的硬化系数K变成了损伤后的（1-D）K。如图3-16，Ⅰ、Ⅱ、Ⅲ阶段分别对应式（3-22）中的第一、二、三式。第Ⅰ阶段为弹性阶段，第Ⅱ阶段为屈服阶段，应力值为屈服极限，第Ⅲ阶段为考虑损伤的塑性强化阶段。由于焊材循环加载控制应变值较小，故首次加载曲线并不会到达下降段。式（3-22）为首次加载曲线模型表达式。

图3—15　焊材首次加载应力-应变典型试验曲线图

图3—16　焊材首次加载曲线模型

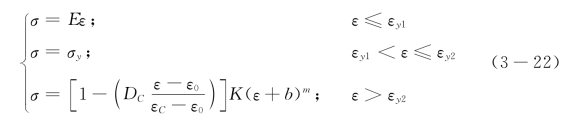
模型中参数通过单向拉伸试验结果进行拟合，如图3-17为部分试件拟合情况，最终拟合结果见表3-5。

表3-5　焊缝首次加载曲线模型最终参数取值

图3—17　焊材应力-应变试验值与本构模型拟合

2．基于Ramberg-Osgood模型的焊材循环应力-应变曲线

将不同应变幅控制下的应力-应变滞回曲线置于同一坐标系，将其应力最大和最小峰值点相连，即获得循环应力-应变曲线，如图3-18所示。该曲线并不代表焊材在循环荷载作用下的真实应力-应变路径，是稳定状态下的循环应力-应变曲线。图3-19为焊材试件稳态时的循环应力-应变曲线。

图3—18　循环应力-应变曲线

图3—19　焊材稳态循环应力-应变曲线

研究表明［62］，稳态的循环应力-应变曲线与单调加载时的σ-ε曲线存在差别。焊材属于循环软化材料。其单调加载时的本构关系曲线位于循环应力-应变曲线的上方。如图3-20，焊材低周疲劳试验结果表明，其在循环荷载作用下屈服前的循环应力-应变曲线部分呈线性，与单向荷载作用下的弹性应力-应变关系相吻合。屈服以后，强化部分曲线可用Ramberg-Osgood［63-65］模型进行较好拟合。曲线表达式如式（3-23），模型参数取值由焊材低周疲劳试验获得的数据进行拟合。拟合结果如表3-6。其中公式第一部分弹性模量E0取单调拉伸试验获得的结果。

如图3-20，焊材循环应力-应变曲线按式（3-23）进行拟合，其中，E0、K0、n0分别为初始弹性模量、硬化系数、硬化指数，根据单调拉伸试验和低周疲劳试验数据拟合曲线在σ＞0和σ＜0段基本对称，如式（3-24）～（3-25）对式（3-23）两边取对数对其参数进行拟合。

图3—20　焊材循环应力-应变曲线拟合模型

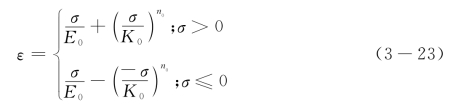
对式（3-23）第一式两边取对数

令，x＝lnσ，b＝-n0 ln K0，则式（3-24）转化为式（3-25）

按式（3-25）进行线性拟合，拟合结果见图3-21，式（3-25）中参数取值如表3-6。

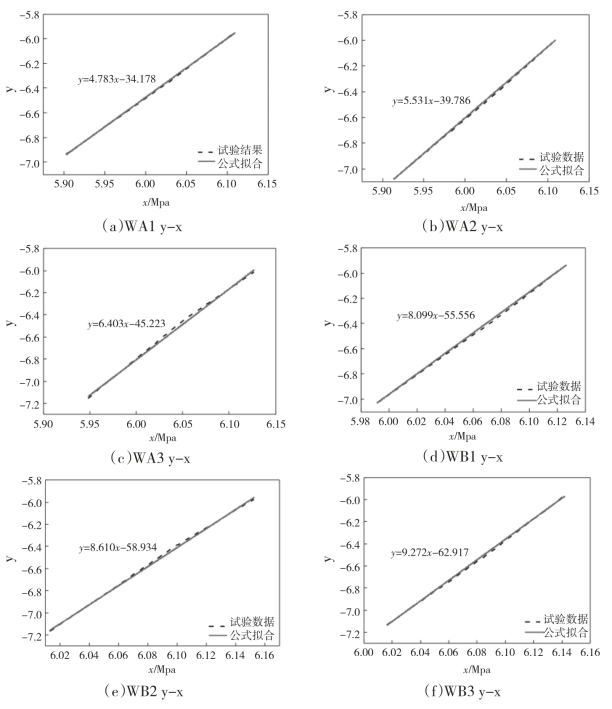
图3—21　焊材循环应力-应变曲线拟合结果

表3-6　焊材循环应力-应变曲线模型参数拟合结果

3．滞回曲线模型(www.daowen.com)

（1）模型探讨

循环应力-应变曲线只能描述循环稳定状态下的σ-ε关系，无法描述循环应力-应变路径，无法反应瞬态应力-应变响应。在稳态循环应力-应变曲线研究基础上，考虑循环过程损伤累积，构造焊材滞回曲线模型。

焊材属于循环软化材料，在循环荷载作用下损伤退化主要体现在应力幅值退化和卸载弹性模量退化，且具有不可逆特性，同时考虑拉压半循环的不完全对称，滞回模型的损伤退化按半循环考虑。常用于描述金属材料的循环本构模型中，理想弹塑性模型、双折线模型、等向强化模型等存在一定局限，无法体现循环荷载作用下焊材的损伤退化行为，与循环大变形下焊材的材料行为存在一定差别。如图3-22a以双折线等向强化模型为例，在常应变幅加载时滞回曲线完全重合，而实际中往往会发生刚度变化、承载力退化、循环硬化或软化等损伤累积线性及非线性强化等，如图3-22b所示。故有必要在现有金属材料本构模型的基础上构造考虑损伤累积影响的焊材滞回曲线模型，用于循环荷载作用下的力学性能分析。

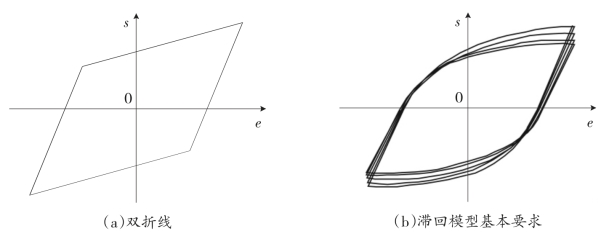
图3—22　不同应力-应变本构关系控制下的滞回曲线

沈祖炎［68］考虑损伤累积影响，提出一种钢材的滞回模型如图3-23a，将半循环滞回曲线划分为三部分，卸载部分和强化部分近似线性模拟，中间再加载部分采用抛物线的形式。该模型用应力幅值和卸载刚度退化的形式考虑了损伤在循环过程的体现，但是并未考虑非线性强化的影响。

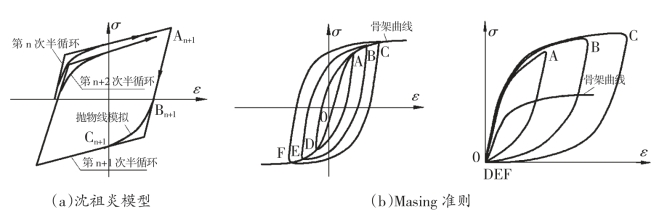
图3—23　常用于描述滞回曲线的模型及准则

石永久［69］［70］提出了考虑钢材损伤退化的钢材等效本构模型，骨架曲线和滞回准则三部分，主要包括初始加载曲线、充分考虑到等幅和逐级加载均使损伤退化出现。模型主要考虑钢框架中梁板端受弯时的损伤，只在滞回曲线受压段引入下降段考虑损伤。

王元清［71］结合Ramberg-Osgood模型得到了SN409B钢材在循环荷载下的循环骨架曲线模型，验证了Ramberg-Osgood模型在钢材中的良好适用性。表达式如式（3-26），其中，E、K、n分别为弹性模量、强化系数、强化指数。

Ramberg-Osgood模型被诸多研究证明可以较好描述金属材料骨架曲线模型，且据Masing准则［62］表明，循环荷载作用下瞬态的应力-应变路径可将稳态时循环应力-应变曲线放大1倍描述。关于Masing准则在1926年最早提出，其含义如式（3-27）和图3-23b。孙伟、陈以一［72］等基于Ramberg-Osgoo模型和Masing准则拟合了Q460钢滞回曲线模型。韩淼［63］基于Masing准则和改进的Ramberg-Osgood模型模拟了一种U型阻尼器滞回曲线模型。迟世春［73］则基于Ramberg-Osgood模型模拟了适用于筑坝土石料的滞回曲线模型。以上研究均表明了Ramberg-Osgood模型和Masing准则在描述钢材滞回曲线模型方面的良好适用性。但是同类研究在构造材料滞回曲线模型时并未考虑到损伤累积的影响。

式（3-27）中，假设骨架曲线方程为σα＝σα（εα），（εr，σr）为滞回曲线卸载起始点坐标，常为应力峰值点。

Chaboche混合强化本构模型［66］［67］常用于描述金属材料循环本构关系。该模型采用Von Mises屈服准则，其混合强化准则同时包含非线性随动强化部分和等向强化。本书以该思想为基础，考虑循环荷载作用过程的损伤累积影响及非线性强化，在上述滞回曲线模型研究的基础上，构造焊材损伤累积滞回曲线模型，其中非线性段结合Ramberg-Osgood模型和Masing准则，在稳态时应力-应变曲线模型的基础上构造。

（2）滞回模型建立

图3—24　循环荷载作用下焊材考虑损伤累积影响的滞回模型

如图3-24，为焊材损伤累积滞回模型，包括首次加载曲线、卸载曲线、再加载（循环加载）曲线。图中包含3个半循环，分别是第n次，（n＋1）次，（n＋2）次，小箭头表示循环指向。以第n次半循环为例：①An-Cn-Bn曲线为第n次半循环的循环加载曲线，考虑非线性加载和强化，An为第n次半循环加载起点，Bn为第n次半循环加载曲线终点，同时为第n次半循环卸载曲线起点，Bn纵坐标为第n次半循环应力峰值；损伤发生后，每个半循环应力峰值进行退化，即应力峰值为包含损伤的应力峰值，其表达式如式（3-28），σm为损伤发生前循环应力幅值，通过稳态循环应力-应变曲线（骨架曲线）模型表达式计算得到，Yn第n次半循环屈服点。②Bn-An＋1为卸载曲线，卸载时近似弹性，当损伤开始时，材料伴随卸载刚度退化，卸载曲线弹性模量为损伤后的弹性模量，其表达式如式（3-29），E0为损伤发生前弹性模量初始值，由单向拉伸试验获得，见表3-6；Bn点为第n次半循环卸载曲线起点，An＋1为第n次半循环卸载曲线终点，同时为第（n＋1）次半循环加载曲线起点。参考文献［61］按（3-28），（3-29）进行损伤退化，Dn为前n次半循环累积损伤变量值，按式（3-21）损伤累积演化方程计算。η、ξ、g、h为参数，通过低周疲劳试验数据进行拟合。

如图3-24为滞回模型及所包含的滞回准则，模型各段曲线表达式如下。

（1）卸载曲线（线性段）

滞回模型卸载曲线部分可用线性关系表示：

σn、εn分别为第n次半循环时曲线任一点应力、应变值。tn为确定曲线形状的参数，其表达式推导如下：

卸载曲线过点，斜率为损伤弹性模量，则可得其表达式如式（3-31），当等应变幅加载时εB为加载应变幅值，为定值。为第n次半循环损伤后应力幅值，按式（3-28）计算。

（2）加载曲线（非线性段）

加载曲线从加载起始点到应力极值点为非线性加载及强化段，Masing准则［62］表明，循环荷载作用下瞬态的应力-应变路径可将稳态时循环应力-应变曲线放大1倍描述。为此，结合文献［63-65，71，73］，在Ramberg-Osgood模型基础上，进行变换，并引入损伤变量描述损伤退化过程，构造循环再加载曲线段模型表达式，如式（3-33）。

其中，σn和εn为第n半循环滞回曲线上应力、应变值和按式（3-28）和式（3-29）进行退化，K′和n′焊材由低周疲劳试验数据进行拟合，该模型表达式在Ramberg-Osgood和Masing准则的基础上考虑了损伤累积和损伤退化的影响。

综上，焊材损伤累积滞回模型表达式如下：

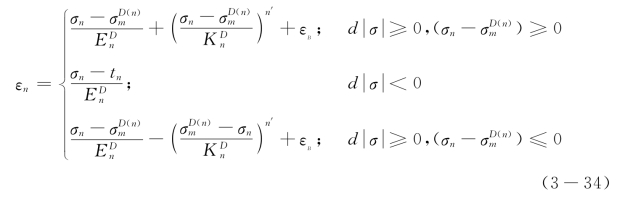
由（3-28），（3-29）和（3-34）共同描述滞回模型，从第2个半循环开始考虑损伤的影响，第一半循环不考虑应力幅、弹性模量的损伤退化。承载力退化和刚度系数退化过程都引入损伤变量来实现，其表达式见（3-21），从其物理意义看，损伤变量演化方程包含了累积能量耗散，将其用于构造滞回模型，使损伤累积体现在滞回准则中。其次，模型中弹性模量和应力幅值退化的不可逆性也反映了损伤的不可逆性。考虑损伤累积后的滞回曲线模型，无论在常幅循环还是变幅循环中，均可以反映循环荷载作用下材料的损伤退化特性及非线性强化过程。其滞回准则实现基本过程：由骨架曲线模型和初始加载曲线计算得到循环加载初始应力幅值→由损伤累积演化方程计算每半循环的损伤变量值D→利用损伤变量D计算得到第n半循环损伤退化后应力幅值、损伤弹性模量→代入（3-34）求得滞回模型各参数→得到第n半循环滞回曲线表达式→以此类推。