低周疲劳循环荷载作用下，焊材损伤不断累积，最终导致破坏。损伤力学中用损伤变量D表示损伤，其定义为受损后不能承载的面积与受损前材料承载面积之比。有效承载面积减小导致单位面积净应力即有效应力增大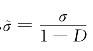为材料受损后有效应力与无损名义应力的关系。

实际研究中很难直接通过定义获得损伤变量值，且往往需要得到损伤变量的表达式用来预测损伤发生程度和用于其他力学关系式的建立。在循环荷载作用下，通过建立损伤变量演化方程来描述损伤累积规律。

1．损伤变量演化方程推导方法

循环荷载作用下，损伤可以看做是一个能量不断耗散的过程。根据损伤力学理论，对于一个耗散系统，若能确定耗散势函数的表达式，则损伤变量作为其状态变量表达式就可以求得。

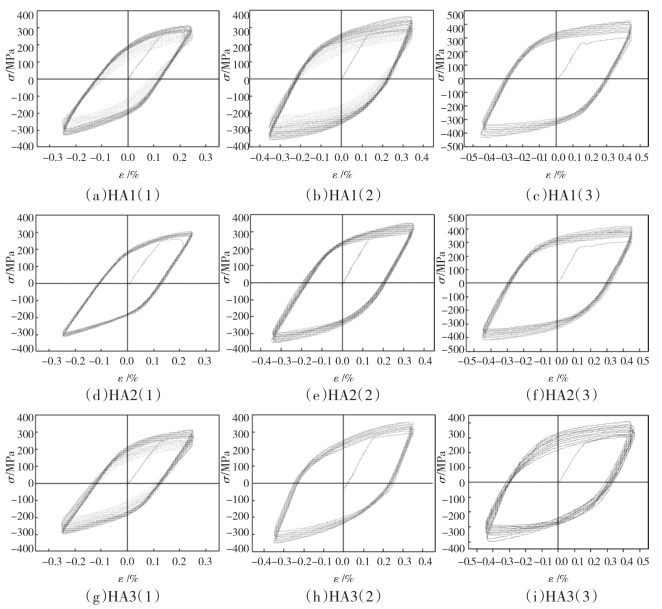
图3—12　Q235热影响区试件应力-应变（σ-ε）滞回曲线

依据损伤力学基本理论，耗散势函数由3部分组成，如式（3-3）：

其中，第一部分φp表示塑性或粘塑性部分；第二部分φD表示损伤耗散部分；第三部分φκ代表微塑性耗散部分；Y是损伤耗能率，D对偶的广义应力，p、κ分别为累积塑性应变和累积微塑性应变。

损伤变量D的演变方程需具备的特性主要有：1）损伤是不可逆的过程，即损伤具有不可恢复性；2）损伤存在门槛值，即存在初值，D＝0对应理想无损状态，D＝1代表结构完成破坏。3）不同荷载下的损伤呈非线性累积。根据不可逆热力学理论，损伤变量D可以作为耗散势函数的一个内变量进行推导，文献［15］给出了由损伤引起能量耗散的耗散势函数的表达式如式（3-4）：

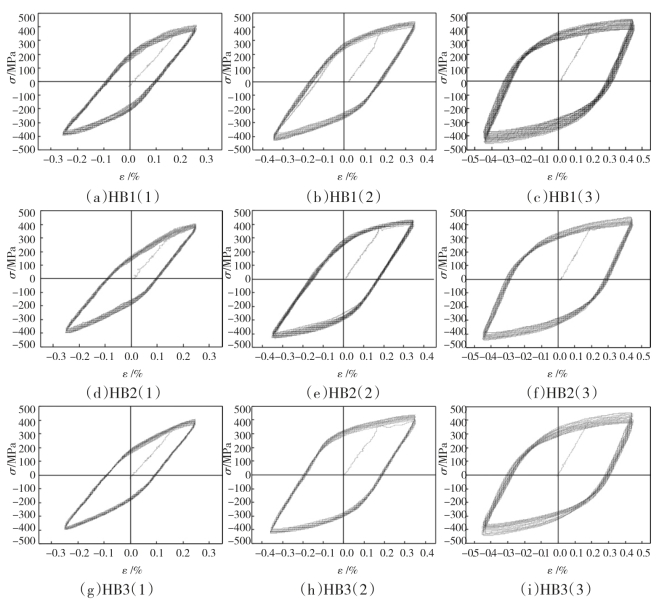
图3—13　Q345热影响区试件应力-应变（σ-ε）滞回曲线

式中，p、κ分别为累积塑性应变和累积为塑性应变；Y是损伤耗能率，D对偶的广义应力，表达式为：

其中，RV的表达式如下：

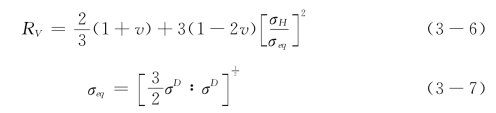
式中σH为各项相等的平均正应力，为Von Mises等效应力，σD为偏应力张量，即有σH＋σD＝σ。结合以上各式，损伤变量D的动态方程如式（3-8）：

忽略微塑性，将（3-5）代入（3-8），采用塑性屈服条件σeq／（1-D）＝σy，并取α＝0，得到塑性损伤模型：

其中累积塑性应变p具有门槛值，p≥p0时损伤开始发生。当处于单轴应力水平时，累积塑性应变即为塑性应变即p＝εp，考虑塑性阶段的损伤时可以大致忽略弹性应变，故p＝ε，且有RV＝1，对（3-9）式积分有：

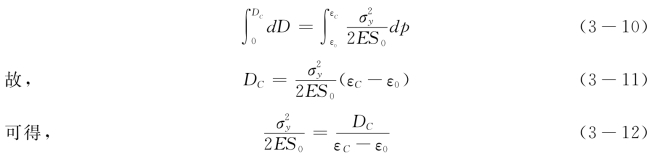
DC为损伤极限到试件断裂时的损伤变量值，εC为对应应变值。将（3-12）式代入（3-9）式积分：

考虑达到损伤极限时损伤变量值近似取1。式（3-13）中，（εC-ε0）看作材料最大塑性应变，由单向拉伸试验可以获得。塑性应变开始累积时损伤发生，故累积塑性应变初始值P0可取0。P为累积塑性应变，在循环荷载作用下，每次循环都将产生永久塑性应变，令Pi为第i次循环循环累积塑性应变为第i次循环产生的塑性应变，则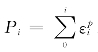。拉压低周疲劳试验中，每个半循环可看作是一次单拉或者单压，半循环内RV取常数λ，将i记作半循环周数，将式（3-13）离散为式（3-14）：

当λ为定值时，式（3-14）变成式（3-15），并计入起始损伤周数i0：

以上为根据损伤力学理论对低周疲劳损伤变量方程的推导过程，推导过程和结果也表明，循环荷载作用下，塑性应变累积是引起损伤累积的重要因素。损伤累积演化方程将在此基础上结合目前研究所得损伤变量计算方程进行确定。

当处于单调加载情况时，由（3-13）可以推导得到，其中，DC可以根据损伤变量的定义求得。

2．常用损伤变量计算方程

损伤累积的过程较为复杂，存在很多影响损伤变量的因素，多年来针对损伤变量的研究大致是从以下几方面考虑的：①考虑从变形角度来构造损伤变量表达式；②考虑从能量耗散的角度推导损伤变量方程；③从变形和能量耗散两方面综合考虑。(www.daowen.com)

（1）变形方面

早期，Powell和Allahabadi［55］通过研究获得结论，认为从变形着手推导的的损伤变量表达式简单、合理。

·Krawinkler模型-Krawinkler［56］针对H型截面悬臂梁进行了循环加载试验，获得了用半循环位移与屈服位移之比表示损伤变量的模型，如式（3-16）

其中，μ为半循环最大位移与屈服位移之比，α为试验获得的参数，此模型为基于变形表示的损伤变量方程的实例。

·沈祖炎模型-沈祖炎［57］从变形角度，提出了用于循环荷载作用下，由累积塑性应变表示的损伤变量演化方程，如式（3-17）

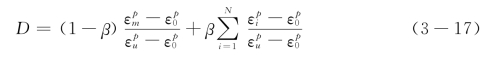
式（3-17）中为循环过程最大塑性应变为材料极限塑性应变，可以通过单向拉伸试验获得。该表达式满足结构破坏时损伤值为1的条件，且从物理意义来看，考虑损伤累积由塑性应变累积引起，符合实际，表达式能够反映出损伤累积的效果。另外，该式考虑到了最大塑性变形的影响，权值为（1-β）。

（2）能量方面

·Kumar模型-Kumar［58］用塑性能的耗散比例表示损伤演化方程，如式（3-18），认为当结构破坏时能量耗散完。

其中，Ei为第i个半循环的能量耗散量，Eu为单调加载时的极限滞回能。

（3）综合考虑变形和能量

·Park-Ang模型-综合考虑到变形和能量耗散推导的损伤累积模型，由Park-Ang［59］提出，如式（3-19）。

该模型最初基于地震荷载作用下提出，δm、δu分别表示地震作用下的最大变形和构件或材料的极限变形为累积塑性耗能，Fy为屈服强度，δu为极限变形，Fyδu相当于理想弹塑性时单调荷载作用下的极限滞回能。

该模型物理意义明确，有试验依据，一直被广泛使用。但也存在一定缺陷：①能量部分局限于适用理想弹塑性的情况；②当结构破坏时，D应该为1，但此式计算结果大于1。

·Usami模型-Usami针对Park-Ang模型的缺陷提出了一个改进模型，如式（3-20），该模型克服了D可能大于1的缺陷，但仍具有计算参数困难等缺陷。

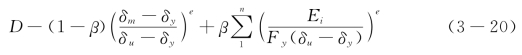
以上常用到的损伤变量方程着眼于变形、能力，变形和能力综合考虑方面均有各自的优点和缺点，适用于不同的损伤累积情况。他们的共同点是，都可以反映损伤累积的过程和损伤演化规律。也可以看出，在循环荷载作用下，塑性应变累积和耗能累积是引起损伤累积的主要原因，故损伤变量的建立多从这两方面着手。

3．损伤累积演化方程

结合损伤力学理论进行的损伤变量演化方程推导过程和现有常用损伤变量计算模型，在Shen和Park-Ang模型的基础上，确立用于循环荷载作用下焊材损伤变量的计算公式即损伤累积演化方程［60］［61］，如式（3-21）。考虑到焊材属于循环软化材料，但初始几次有循环硬化现象，故损伤起始周数不再从0开始。

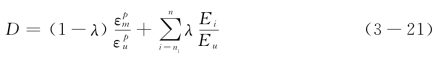
式（3-21），综合考虑塑性应变和累积塑性耗能对焊材损伤累积的影响。其中，各物理量含义如下：

——循环中最大塑性应变；

——材料极限塑性应变，通过单调拉伸试验结果可以确定，即

Ei——第i半循环塑性变形能耗散值，如图3-14。为焊材第m个循环能量耗散示意图，其中，①为塑性应变能，②为弹性应变能，③为损伤耗散能，③与①之间的分割线斜率代表损伤发生前弹性模量值，则为第n个半循环累积塑性耗能。

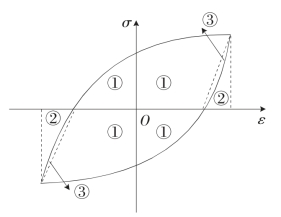
图3—14　焊材第m循环能量耗散示意图

Eu为单调荷载作用下极限滞回能，为单调加载到破坏时应力-应变曲线与坐标轴所围面积，通过单调拉伸应力-应变关系曲线积分获得，不再局限于理想弹塑性的情况。

λ为第i周塑性耗能权值，（1-λ）为最大塑性应变引起的损伤所占权值，其值可通过试验结果计算获得。即令试件破坏时D＝1，计算此时最大塑性应变值和累积塑性耗能，代入式（3-21）可解出λ＝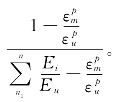

式（3-21）所示损伤变量演化方程，包含塑性能累积，表现了损伤累积的过程。综合考虑了从能量和变形入手构造损伤演变方程，同时保证了当结构和材料破坏时，D基本为1，不会出现D大于1的情况。其次单调加载时的极限滞回能不限制于理想弹塑性的情况。