随着CAD／CAE／CAM技术的日益成熟和计算机技术的不断发展，有限元法及其软件的开发和应用价值日益突显。尤其对于复杂建筑结构体系的仿真模拟变得容易。

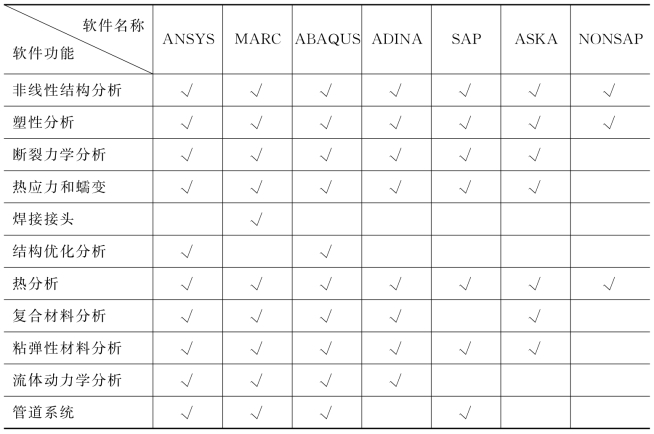
在建筑结构分析方面，目前最常用的有限元商业软件有ANSYS、ABAQUS和PATRAN／MARC等，这些软件均能建立几何和材料非线性来进行管桁结构搭接节点区域复杂应力和节点极限承载力的计算。其基本的功能特点如表2-3所示［46］。

从表2-3中可以看出，各种分析软件的功能各具特色，对于结构的非线性数值模拟基本能够满足使用要求。在建立计算分析模型方面，PATRAN／MARC软件过于精细和复杂，需要的计算内存约3倍于ANSYS计算所需内存；对于非线性求解能力及计算精度较高方面，ABAQUS的优势明显，但从易用性上其优势不如ANSYS；ANSYS所独有的APDL语言包使得ANSYS建模参数化、过程求解以及后处理方面都较为方便，非常有利于非线性大变形弹塑性计算和大量的有限元参数分析［47］。

表2-3　常用有限元软件及其功能

钢管节点滞回性能的数值模拟主要使用了ANSYS分析软件的非线性分析功能。ANSYS单元库中有超过100种的单元类型，可以针对所分析的问题选取相适用的单元类型［48］［49］。

1．分析单元的选取

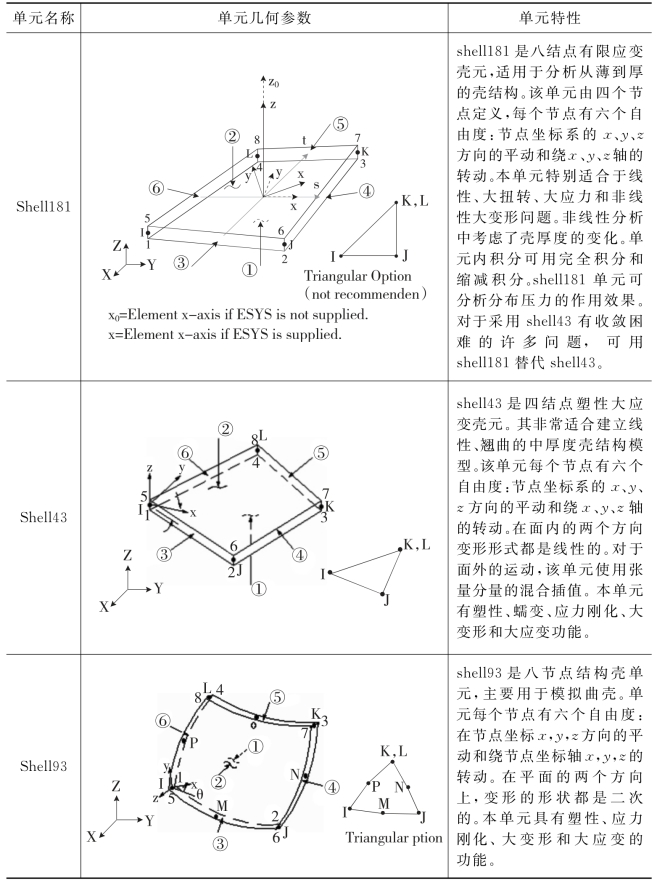
钢管节点是多管相贯构成的空间壳体，在数值模拟分析中分析单元大多采用弹塑性壳单元，实体单元的计算精度虽然高，但耗时，而采用弹塑性壳元，能够满足分析精度。大多数ANSYS分析中单元采用shell181、shell93、shell43．他们各自的性能如表2-4所示。

文献［50］采用Shell43来模拟钢管节点的力学性能，结果发现：在以位移控制的往复荷载作用下计算很难收敛，而单元Shell181收敛容易，并且两种单元计算结果吻合得很好。文献［51］分析比较了Shell181与shell93这两种计算单元的不同，通过对一个平面K节点的比较分析，两种单元建模的节点承载力较为接近，两者都接近于试验值，但shell181单元建模计算的时间短，效率高。

2．非线性方程求解［47］［52］［53］

（1）基本假定

在对管桁搭接节点所建立的非线性方程进行求解时，为简化计算，做以下假定：

表2-4　ANSYS有限元中shell181、shell93、shell43特征对比

平行于中面的各层互不挤压，即垂直于中面的应力忽略不计；垂直于中面的直线变形后仍保持直线；挠度沿板厚度的变化忽略不计，认为在同一厚度方向上各点的挠度都等于中面的挠度，即薄板大挠度假定；假定材料的硬化模量为弹性模量的0．5%。

（2）求解方法

对于工程结构中的非线性问题求解，ANSYS程序的求解器通过计算一系列联立线性方程来解决。若结构的非线性行为直接用这样一系列的线性方程表示并求算，难度是非常大或者说是做不到的。为此，需要采用一系列带校正的线性近似来求解非线性问题。一般采用以追踪结构整个变形历程的增量迭代法。增量迭代法有：虚加刚性弹簧法、Newton-Raphson方法、弧长法和位移控制法等。

①Newton-Raphson方法

其基本原理为：先将荷载分为一系列的荷载增量步，然后在该荷载增量步结束时的平衡构形上进行下一个荷载增量步的求解。为消除累计误差，N-R法强迫在某个允许范围内的每一个荷载增量的末端，解答都能达到平衡收敛。图2-4（a）为其求解过程。(www.daowen.com)

②弧长法

弧长法是在求解过程中同时控制荷载增量和位移增量水平，使迭代沿一段弧收敛的双重目标控制方法，图2-4（b）显示了弧长法求解过程。

图2—4　New ton-Raphson法和弧长法求解示意

在非线性方程组的求解过程中，当使用N-R方法，正切刚度矩阵可能变为降秩矩阵，导致严重的收敛问题时，利用弧长法可以帮助稳定求解。用此方法使N-R平衡迭代沿一段弧收敛，即使当正切刚度矩阵为零或负值时，也可以阻止发散。

为增强研究问题的收敛性，ANSYS程序也提供了一系列命令，如线性搜索、自适应下降、自动载荷步及二分法等，通过激活这些命令来加强问题的收敛性，若不能得到收敛，则程序将终止计算。

（3）收敛准则

在进行迭代求解过程中，收敛的判别准则通常有以下三种方法：①增量理论判据；②不平衡节点力判据；③位移增量判据。本文采用后两种方法作为收敛判断的依据。

I．不平衡节点力判据

式中：——在某级荷载下经i次迭代后不平衡节点力向量的范数

——在同级荷载下，第i次迭代时附加荷载所产生的等效节点力向量范数

α——收敛误差容限，本文取0．001

II．位移增量判据

式中：——在某级荷载下，经前后两次迭代后的节点位移向量的无穷范数之差

——在同级荷载下，前次迭代后的节点位移向量的无穷范数

α——收敛误差容限，取0．001