常见非线性问题有几何非线性和材料非线性。从本质上来讲，工程中结构问题都会遇到非线性情况。用于力学分析时，常用到的弹性假设、小变形假设、边界条件线性假设等将结构分析问题简化到了线性分析范围。但是当结构涉及大变形时往往不能忽略几何非线性，当材料发生较大塑性变形时，应力-应变关系不在符合弹性阶段的胡克定律，不能忽略材料非线性。在有限元分析中，求解非线性方程组无法采用直接求解方法，需要用数值解法，几何和材料非线性往往会给计算过程带来一定难度。

（1）几何非线性

往往在小变形假设下，力学平衡方程建立时并不考虑结构体已产生的变形，大变形时，需要考虑几何非线性的影响，平衡方程建立在结构体发生变形的情况下。当考虑大变形情况时，分两种情况，大变形小应变以及大变形大应变，通常遇到的情况需考虑大变形小应变，即材料处于弹性状态时无需重新考虑应力-应变关系。考虑几何非线性时，结构分析中涉及变形的方程不能再像小变形假设时忽略高阶位移分量，例如钢结构大变形稳定性分析。

在有限元分析方程建立中，几何非线性表现为切线刚度矩阵与位移之间表现为非线性关系，导致基本方程组不再是线性方程组，需要使用层层逼近的近似数值方法求解，增加有限元计算的空间和时间复杂度。非线性有限元分析对于数值分析模型、材料模型及有限单元的划分精度有较高的要求。如图2-1，P-△效应和P-δ效应为两种常见几何非线性情况，P-△是由于结构体侧向变形引起的重力附加效应，P-δ是由于在轴向力作用下结构体自身发生挠曲产生的附加弯矩效应。在有限元分析中考虑两种二阶效应的方法有等效几何刚度法、折减弹性抗弯刚度法、结构位移和构架内力增大系数法等。

（2）材料非线性

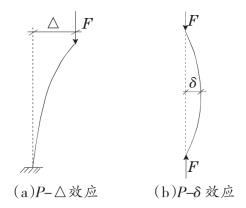
图2—1　几何非线性情况

(www.daowen.com)

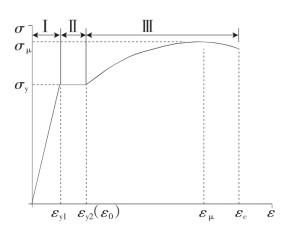
图2—2　常见金属材料本构关系

材料非线性主要由材料应力-应变非线性本构关系引起。对于多数金属材料而言，在弹性阶段，应力-应变基本呈线性关系，服从胡克定律，如式（2-10），当处于单轴应力状态时，应力-应变关系表现为式（2-11），如图2-2的弹性阶段。当材料发生屈服进入塑性阶段后，应力-应变关系不再为简单线性关系，应变状态不但与应力状态有关，而且依赖于整个应力历史，表现出材料非线性特性。式（2-12）为塑性阶段应力-应变关系的增量形式，Sij为应力偏量，G的表达式为式（2-13），dλ为参数，式（2-14）为普朗特推导dλ表达式获得的一种有效塑性本构关系，将应变分为弹性应变分量和塑性应变分量两项。如图2-2为常见弹塑性材料拉伸试验获得的应力-应变关系曲线，第Ⅰ阶段为弹性阶段，应力-应变关系呈线性，斜率为弹性模量E，第Ⅱ阶段为屈服阶段，第Ⅲ阶段材料进入塑性阶段后本构关系呈非线性。

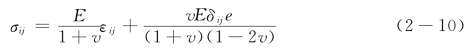
式（2-10）中，ij为下标记号，配合张量符号使用，v为泊松比。

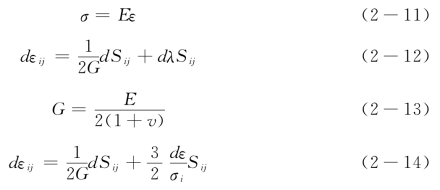
当在有限元分析中考虑塑性阶段材料非线性特性时，有限元方程中［D］矩阵与位移之间关系表现为非线性，非线性方程组无法直接求解，需要通过增量法和迭代法等数值解法进行求解。

有限元分析中存在的非线性问题还有接触非线性、边界条件非线性等，非线性问题的增加会加大分析计算的复杂程度。