开口薄壁截面压弯构件的抗扭刚度及弯矩作用平面外的抗弯刚度通常较小,当构件在弯矩作用平面外没有足够的支承以阻止其产生侧向位移和扭转时,构件可能发生弯扭屈曲而破坏,这种弯扭屈曲又称为压弯构件弯矩作用平面外的整体失稳。

根据弹性稳定理论,对两端支承承受轴心压力和弯矩作用的双轴对称截面实腹式压弯构件,当构件没有弯矩作用平面外的初始几何缺陷(初挠度与初扭转)时,在弯矩作用平面外的弯扭屈曲临界条件可用式(6.18)表达:

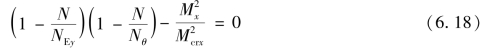
式中　NEy——构件轴心受压时绕y轴弯曲屈曲的临界力;

Nθ——构件绕纵轴z轴扭转屈曲的临界力;

Mcrx——构件绕x轴的均匀弯矩作用时的弯扭屈曲临界弯矩。

式(6.18)可绘制成图6.7形式的相关曲线。根据钢结构构件常用的截面形式分析,绝大多数情况下Nθ/NEy都大于1.0,为安全起见取Nθ/NEy=1.0,则可得到判别构件弯矩作用平面外稳定性的直线相关方程为:

式(6.19)是根据双轴对称理想压弯构件导出并经简化的理论公式。将该式中的NEy和Mcrx分别用φyAfy和φbW1xfy代入,引入等效弯矩系数βtx、截面影响系数η和抗力分项系数并整理后可以得到《钢结构设计标准》(GB50017—2017)计算压弯构件弯矩作用平面外整体稳定的验算公式:

式中　Mx——所计算构件范围内(构件侧向支承点之间)的最大弯矩;

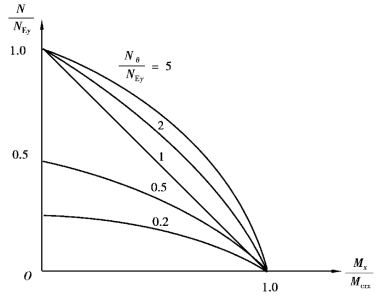
图6.7　单向压弯构件在弯矩作用平面外失稳的相关曲线

η——截面影响系数,箱形截面取η=0.7,其他截面η=1.0;(www.daowen.com)

φy——弯矩作用平面外的轴心受压构件稳定系数,对于单轴对称截面应考虑扭转效应,采用换算长细比λyz确定,对于双轴对称截面或极对称截面可直接用λy确定;

φb——均匀弯曲的受弯构件整体稳定系数,对工字形截面和T形截面可按《钢结构设

计标准》(GB50017—2017)附录中的近似公式计算,对于箱形截面取φb=1.0;

βtx——弯矩等效系数,应根据所计算构件段的荷载和内力情况确定,按下列规定采用:

①在弯矩作用平面外有支承的构件,应根据两相邻支承点间构件段内的荷载和内力情况确定:构件段无横向荷载作用时,βtx=0.65+0.35M2/M1,M1和M2是构件段在弯矩作用平面内的端弯矩,且,当使构件段产生同向曲率时取同号,产生反向曲率时取异号;构件段内有端弯矩和横向荷载同时作用时,使构件段产生同向曲率βtx=1.0;使构件段产生反向曲率取βtx=0.85;构件段内无端弯矩但有横向荷载作用时,βtx=1.0。

②弯矩作用平面外为悬臂构件,βtx=1.0。

弯矩作用在两个主轴平面内为双向弯曲压弯构件,双向压弯构件的整体失稳常伴随着构件的扭转变形,其稳定承载力与N,Mx和My三者的比例有关,无法给出解析解,只能采用数值解。因为当两个方向弯矩很小时,双向压弯构件应接近轴心受压构件的受力情况,当某一个方向的弯矩很小时,应接近单向压弯构件的受力情况。为了设计方便,并与轴心受压构件和单向压弯构件计算衔接,采用相关公式计算。《钢结构设计标准》(GB50017—2017)规定,弯矩作用在两个主平面内的双轴对称实腹式工字形截面(含H形)和箱形(闭口)截面的压弯构件,其稳定按下列公式计算:

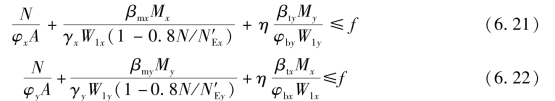
式中　Mx和My——所计算构件段范围内对x轴和y轴的最大弯矩。

φx,φy——对x轴和y轴的轴心受压构件稳定系数。

φbx,φby——均匀弯曲的受弯构件整体稳定系数,对工字形截面的非悬臂构件,φbx可按受弯构件整体稳定系数近似公式计算,φby=1.0;对闭口截面,φbx=φby=1.0。

βmx,βmy——等效弯矩系数,应按弯矩作用平面内稳定计算的有关规定采用。

βtx,βty和η应按弯矩作用平面外稳定计算的有关规定采用。