现以图6.6(a)所示的两端铰接的压弯构件为例,除轴心压力N外,两端各作用有弯矩M。压弯构件由于轴心压力和弯矩的同时作用,在弯矩作用平面内一开始就产生弯曲变形,压力—挠度曲线如图6.6(b)中的oabc所示。oa段为弹性工作阶段,但由于附加弯矩N·y的存在而呈现非线性关系;a点之后进入弹塑性工作阶段,曲线ab段呈现上升状,挠度随N的增加才能增加,此时平衡是稳定的;在bc段为了维持平衡,N要不断减小,且挠度不断增加,平衡是不稳定的。b点为稳定平衡状态过渡到不稳定平衡状态的曲线极值点,与之对应的Nu值为构件在弯矩作用平面内的稳定极限承载力,相应的截面平均应力称为极限应力。

单向压弯构件在弯矩作用平面内的稳定计算方法目前有3种,即按边缘纤维屈服准则的方法,按极限承载能力准则的方法和实用计算公式。下面介绍《钢结构设计标准》(GB50017—2017)采用的边缘纤维屈服准则。

边缘纤维屈服准则的方法是用应力问题代替稳定计算的近似方法,即以构件截面应力最大边缘纤维开始屈服时的荷载,亦即构件在弹性阶段的最大荷载,作为压弯构件的确定承载力。以图6.6(a)为例,该准则的表达式为:

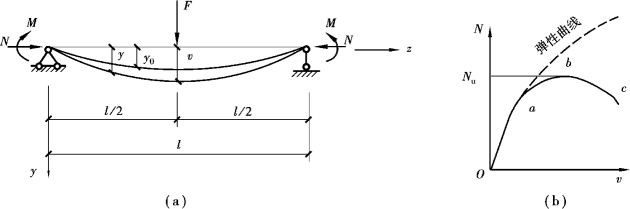
图6.6　单向压弯构件在弯矩作用平面内的整体屈曲

式中　N——轴心压力;

Mmax——考虑N和初始缺陷影响后的最大弯矩;

A——构件的毛截面面积;

W1x——构件较大受压边缘的毛截面抵抗矩。

在轴心压力N和弯矩M共同作用下,构件中点的挠度为v,在离端部x处的挠度为y,此处的平衡方程为:

令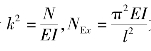为欧拉临界力,则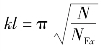,求解方程可得:

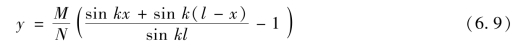
构件中点的最大挠度为:

构件最大弯矩位于中部截面,其值为:

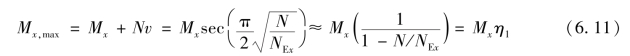
式中　η1——压弯构件的挠度增大系数;

Mx——构件的端弯矩,Mx=Ne。

其他几种常见荷载作用下的压弯构件,其最大弯矩Mx,max,i=ηiMx的近似值见表6.1。其弯矩等效系数βmi可按式(6.12)计算:

(www.daowen.com)

表6.1　压弯构件的最大弯矩与等效弯矩系数

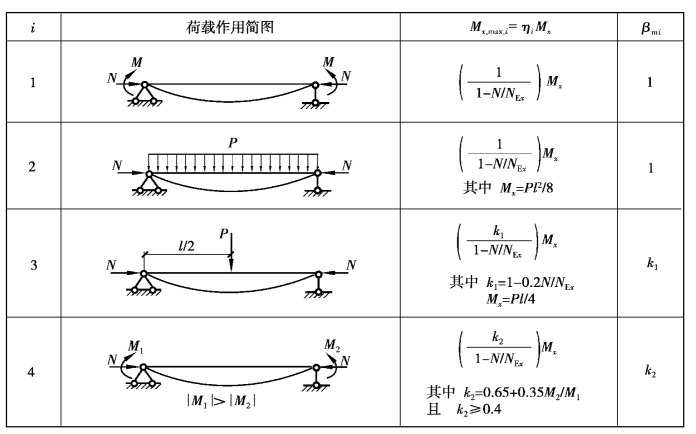
利用βmi可以在弯矩作用平面内的稳定计算中,把各种荷载作用的弯矩分布形式转化为均匀受弯来对待,考虑构件初始缺陷后,把最大弯矩值代入式(6.7)中,可得到:

式中,e0是用来考虑构件综合缺陷的等效初弯曲。当M=0时,构件实际上即为带有缺陷偏心e0的轴心受压构件,此时构件的临界力N=Nx=φxAfy,由式(6.13)可得到:)

将式(6.14)代入式(6.13),经整理后得:

为了限制偏心或长细比较大构件的变形,只容许截面塑性发展的总深度不超过截面高度的1/4。根据对11种常见截面形式进行的计算比较,《钢结构设计标准》(GB50017—2017)对式(6.15)作了修正,用来验算实腹式压弯构件在弯矩作用平面内的稳定性:

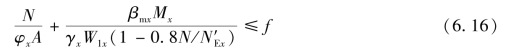
式中　;

φx——弯矩作用平面内的轴心受压构件稳定系数;

Mx——所计算构件范围内的最大弯矩;

βmx——等效弯矩系数。

对于单轴对称截面压弯构件,当弯矩作用在对称轴平面内且使较大翼缘受压时,构件达到临界状态时的应力分布可能在拉、压两侧都出现塑性铰,也可能只在受拉一侧出现塑性铰。对于前者,平面内的稳定仍按式(6.16)验算;对于后者,因受拉塑性区的开展会导致构件失稳,因此除按式(6.16)计算外,还应按式(6.17)计算:

式中　W2x——受拉一侧的边缘纤维毛截面模量。

βmx可按以下规定采用:

①悬臂构件和在内力分析中未考虑二阶效应的无支撑框架和弱支撑框架柱,βmx=1.0。

②框架柱和两端支承的构件:无横向荷载作用时,βmx=0.65+0.35M2/M1,M1和M2分别是构件两端的弯矩,且,当两端弯矩使构件产生同向曲率时取同号,使构件产生反向曲率(有反弯点)时取异号;有端弯矩和横向荷载同时作用时,使构件产生同向曲率时取βmx=1.0,使构件产生反向曲率时取βmx=0.85;无端弯矩但有横向荷载作用时,取βmx=1.0。