对于拉弯构件和截面有孔洞等削弱过多的构件以及构件端部弯矩大于跨间弯矩的压弯构件,需要进行强度计算。

考虑钢材的塑性性能,拉弯和压弯构件是以截面出现塑性铰作为其强度极限状态。在轴心压力N和弯矩M的共同作用下,矩形截面上应力的发展过程如图6.4所示。假设轴线力不变而弯矩不断增加,截面上应力的发展经历4个阶段:

①边缘纤维的最大应力达到屈服点,如图6.4(b)所示。

②最大应力一侧部分截面发展塑性,如图6.4(c)所示。

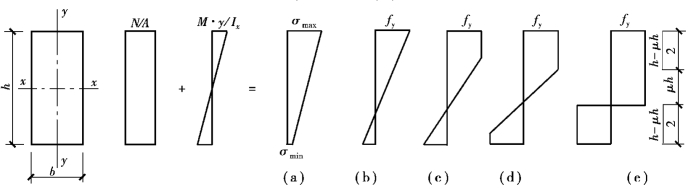
图6.4　压弯构件截面应力的发展过程

③两侧部分截面均发展塑性,如图6.4(d)所示。

④全截面进入塑性状态出现塑性铰,如图6.4(e)所示,此时达到承载能力的极限状态。

当构件截面出现塑性铰时,根据力的平衡条件可得到如下关系式:

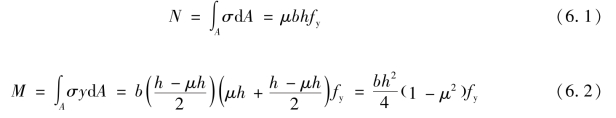
在上面两式中,注意到A=bh,,消去μ,可得到N和M的关系式如下:

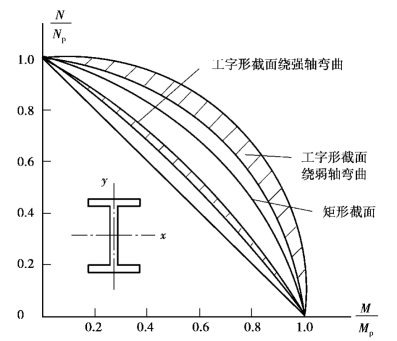
对于工字形截面,也可以用同样的方法求得它们的N和M的相关关系。由于工字形截面翼缘和腹板的相对尺寸不同,相关曲线会在一定范围内变化。图6.5中的阴影区给出了常用的工字形截面绕强轴和弱轴弯曲相关曲线的变化范围。在制定规范时,采用了图中的直线作为强度计算的依据,这样做计算简便且偏于安全:

(www.daowen.com)

图6.5　压弯构件强度计算相关曲线

设计时以An代替式(6.4)中的A,考虑到破坏时仅允许截面出现部分塑性,以γxWnx和γyWny代替式(6.4)中的Wp,引入抗力分项系数后,就可得到实腹式拉弯和压弯构件的强度计算公式。

对于弯矩作用在一个主平面内的单向拉弯、压弯构件:

式(6.5)也适用于单轴对称截面,弯曲正应力一项带有正负号,计算时应使两项应力的代数和的绝对值最大。

对于弯矩作用在两个主平面内的双向拉弯、压弯构件:

式中　An——构件验算截面净截面面积;

Wnx,Wny——构件验算截面分别对x轴和y轴的净截面模量;

γx,γy——截面塑性发展系数,按附录3采用。

当压弯构件受压翼缘自由外伸宽度与厚度之比大于而小于15235/fy时,γx=1.0。

对直接承受动力荷载的构件,不宜考虑截面的塑性发展,取γx=γy=1.0。

拉弯和压弯构件的容许长细比分别与轴心受拉和轴心受压构件的规定完全相同,请参见相关内容。