上述介绍的是理想轴心受压构件的稳定问题,实际轴心受压钢构件的受力性能与理想轴心受压构件有很大不同。以欧拉公式为例,严格来说,其假定均不成立,只不过影响的程度不同而已。实际上,轴心受压构件的受力性能受到许多因素的影响,已有研究表明,实际轴心受压构件必须考虑截面中的残余应力、杆轴的初弯曲、荷载作用点的初偏心以及杆端的约束条件等因素的影响。

1)力学缺陷对轴心受压构件弯曲屈曲的影响

构件中的力学缺陷主要是指残余应力,它的产生主要是由于钢材热轧以及板边火焰切割、构件焊接和校正调直等加工制造过程中不均匀的高温加热和冷却所引起的。其中,焊接残余应力的数值最大,通常可达到或接近钢材的屈服强度fy。

图5.5(a)所示的H型钢,在热轧后的冷却过程中,翼缘板端的单位体积的暴露面积大于腹板与翼缘交接处,冷却较快,而腹板与翼缘的交接处冷却较慢。同理,腹板中部也比其两端冷却较快。后冷却部分的收缩受到先冷却部分的约束从而产生了残余拉应力,而先冷却部分则产生了与之平衡的残余压应力。因此,残余应力是构件尚未承受外荷载之前就已经存在的一种初应力,在一个截面上具有自相平衡的特点。

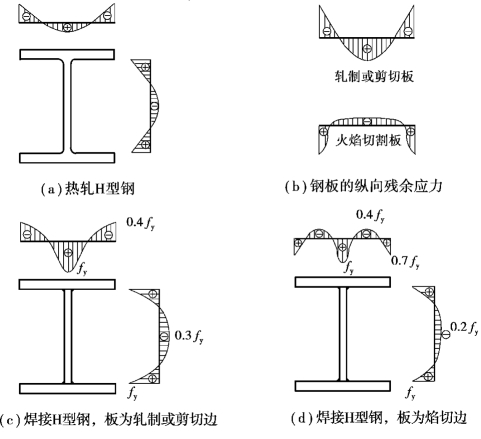
图5.5　构件纵向残余应力的分布

热轧或剪切钢板的残余应力较小,如图5.5(b)所示,常可忽略。用这种带钢焊接组合而成的工字形钢截面,其焊缝处的残余拉应力可能达到屈服点,如图5.5(c)所示。

对于火焰切割钢板,由于切割时热量集中在切割处的很小范围内,在板边缘的一定范围内可能产生高于屈服点的残余拉应力,板的中部则产生较小的残余压应力,如图5.5(b)所示。用这种钢板焊接组合而成的工字形钢截面,在翼缘板的焊缝处变号为残余拉应力,如图5.5(d)所示。

下面分析残余应力对短柱稳定性的不利影响,通常由短柱压缩试验进行测定。所谓短柱是指取一柱段,其长细比不大于10,不致在受压时发生屈曲破坏,又能够保证其中部截面反映实际的残余应力。

现以图5.6(a)例,为使问题简化起见,忽略影响不大的腹板残余应力的影响。如果短柱内不存在残余应力,则其应力-应变曲线与小试件测得的σ-ε曲线相同,接近理想的弹塑性体,如图5.6(b)虚线所示。但是,由于残余应力的存在,在轴心压力N的作用下,残余应力与截面上的平均应力N/A相叠加,将使截面的某些部位提前屈服并发展成塑性变形。假设两翼缘上的残余应力为线性分布,翼缘两外端的最大残余压应力为σr=0.3fy,翼缘中点为最大残余应力。当N/A<0.7fy时,截面上的应力处于弹性阶段;当N/A=0.7fy时,与残余应力叠加后,翼缘端部应力达到屈服点fy,此时短柱的平均应力-应变曲线开始弯曲,该点称为有效比例极限fp=fy-σr;当N/A继续增加超过0.7fy后,截面的屈服逐渐向中间发展,弹性区逐渐减小,直到N/A=fy翼缘全部屈服为止[图5.6(c)]。从图5.6(b)中可以看出,在fp和fy之间出现了一条渐变曲线,此即为残余应力使部分材料提前屈服的结果。由此可见,残余应力对短柱的σ-ε曲线的影响表现在降低了构件的比例极限;当外荷载引起的应力超过比例极限后,残余应力使构件的平均应力-应变曲线变成非线性关系,同时减小了截面的有效面积和有效惯性矩,从而降低了构件的稳定承载力。

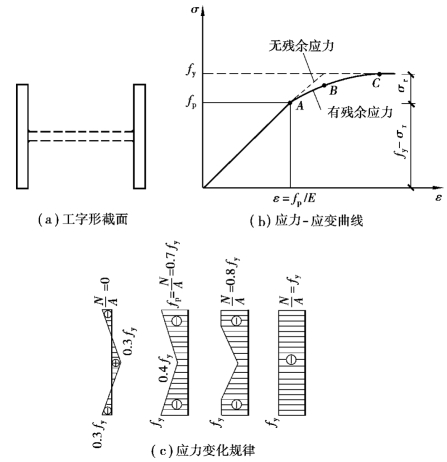
图5.6　残余应力对轴心受压短柱平均应力-应变曲线的影响

若σ≤fp,构件处于弹性阶段,可采用欧拉公式计算其临界力与临界应力。

若fp≤σ≤fy,此时构件在弹塑性阶段工作,截面由变形模量不同的两部分组成,塑性区的变形模量为零,而弹性区的模量仍为E。构件发生微小弯曲时,能够产生抵抗力矩的只是截面的弹性区。因此,只能按截面弹性区的有效截面惯性矩Ie代替全截面的惯性矩I来计算其临界力,即:

相应的临界应力为:

式(5.9)表明,由于残余应力的影响使构件截面提前出现塑性区,从而降低了构件的临界力或临界应力,其值为弹性欧拉临界值乘以小于1的折减系数Ie/I。而比值Ie/I与残余应力的分布和大小、构件截面的形状以及构件屈曲时的弯曲方向有关。

现以图5.7所示的工字形截面为例说明Ie/I的计算。截面的屈服区在翼缘两端有阴影部分,考虑到腹板靠近截面形心轴,计算时忽略其作用。截面弹性部分的翼缘宽度为be,令η=be/b=bet/bt=Ae/A,Ae为截面弹性部分的面积,则:

绕强轴(x—x轴)屈曲时:

绕弱轴(y—y轴)屈曲时:

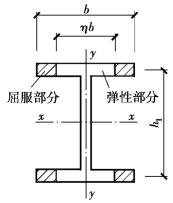
图5.7　屈曲时截面部分屈服

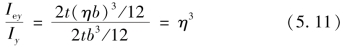
比较式(5.10)和式(5.11)可知,残余应力对临界力的不利影响,随构件屈曲方向而不同。由于η<1,故η3<<η,可见这种截面(屈服区在翼缘的两端)残余应力的不利影响对弱轴屈曲要比对强轴屈曲严重得多。原因是远离弱轴的部分是残余应力最大的部分,而远离强轴的部分则兼有残余压应力和残余拉应力。

2)构件几何缺陷对轴心受压构件弯曲屈曲的影响

实际轴心受压构件不可能是完全挺直的。在制造、运输和安装过程中,构件不可避免地会存在微小弯曲。由于构造、施工和加载等方面的原因,还可能产生一定程度的初偏心。初弯曲和初偏心统称为几何缺陷。有几何缺陷的轴心受压构件,其侧向挠度从加载开始就不断增加,因此构件除轴心力作用外,还存在因构件弯曲而产生的弯矩,从而降低了构件的稳定承载力。

(1)初弯曲对轴心受压构件的影响(www.daowen.com)

首先研究初弯曲的影响。图5.8所示两端铰接、有初弯曲的构件在未受力前就成弯曲状态,假设初弯曲形状为正弦曲线的一个半波,即:

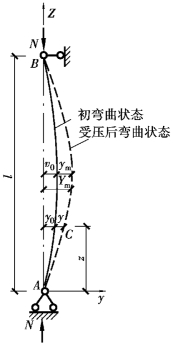
图5.8　有初弯曲的轴心受压构件

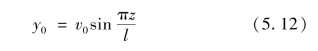
式中　v0——构件中央的初始挠度值,已有的统计资料表明该值为构件几何长度l的1/500～1/2000。

在加载之前,构件任意点C处的曲率为-y″0,作用轴线压力N,构件总的挠度为y,曲率为-y″,在弹性弯曲状态下,根据内外力矩平衡条件可建立平衡微分方程为:

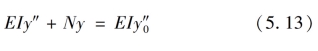
解此方程可得压杆的弹性挠度曲线为:构件中央的最大挠度和最大弯矩分别为

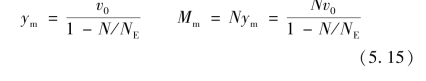
式中　NE——欧拉临界力,;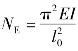

Am——初始挠度放大系数或弯矩放大系数,反映了初弯曲对弹性轴心受压构件的影响,。

任意截面的一阶弯矩为Nv0sin(πz/l),二阶弯矩为AmNv0sin(πz/l),二者之间的差别称为构件本身的二阶效应,简称N-δ效应。

由式(5.14)可知构件的最大挠度ymax不是随着压力N按比例增加的,当压力达到构件的欧拉临界力NE时,对于不同初弯曲的轴心受压构件,ymax均达到无穷大。图5.9中的实线给出了v0=1mm和v0=3mm的轴心受压构件的荷载-挠度曲线,对于弹性构件,曲线均以N=NE为水平渐进线。但实际中的轴心受压构件,当其截面承受弯矩较大时,受力最大的截面边缘纤维开始屈服而进入塑性状态,使得构件的刚度降低,如图5.9中虚线所示。因此,初弯曲降低了轴心受压构件的承载力,其极限荷载与构件截面形式、长细比λ、弯曲方向以及钢材的屈服强度fy有关。

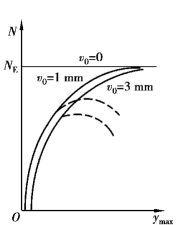
图5.9　有初弯曲的轴心受压构件荷载-挠度曲线

(2)初偏心对轴心受压构件的影响

下面研究初偏心对轴心受压构件的影响。由于构造上的原因和构件截面尺寸的变异,作用在构件端部的轴压力实际上不可避免地会偏离截面的形心而形成初偏心e0,图5.10表示两端铰接、有初偏心e0的轴心受压构件。在弹性弯曲状态下,可建立平衡微分方程如下:

令,可解得:

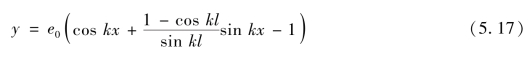
因此,构件中点的最大挠度为:

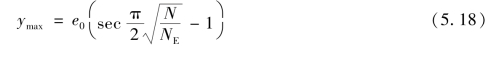
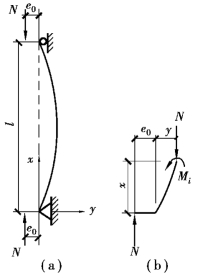
图5.10　有初偏心的轴心受压构件

有初偏心的轴心受压构件的荷载-挠度曲线如图5.11所示,从图中可知,初偏心对轴心受压构件的影响与初弯曲的影响类似,只是在影响程度上有所差别,因此在研究实际构件的承载能力时,常把二者的影响一并考虑。

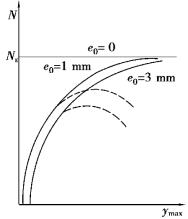
图5.11　有初偏心的轴心受压构件荷载-挠度曲线